am

pour une fois c’est monsieur qui bloggue un concert (et en plus il y prend des photos).

oui bon.
En référence au gateau le plus rapide de l’ouest* qui me procura en son temps ma petite heure de gloire locale :
au bain-marie : 200 g de choc + 120g de sucre + 100g de beurre, quand fondu + 4 oeufs + une cuillère à soupe de farine => 20′ à 160°. (pas mortel, mais pourrait le devenir en glissant au centre un très gros carré de chocolat blanc par exemple)

Faudrait aussi qu’en plus de la playlist que j’ai un peu négligée dernièrement (d’façons je ne sors pas d’une période Nymanesque), je compile une foodlist, histoire de conserver la mémoire de la réalisation d’entre autre ces choses-là :
terrine au potimarron (avec en plus des noisettes)
gateau d’automne au potimarron et aux épices

un jour je retournerai voir des concerts (en attendant, je mange du chocolat - et du potimarron).

* au bain-marie : 200g de choc + 50g de beurre + 5 cuillères à soupe de sucre, quand fondu + 2 oeufs + 5 cuillères à soupe de farines => 15-20 minutes th 6/7. Wünderbar et customisable à volonté.

Je me suis un peu clarifié les idées sur l’optimisation sans contrainte pour les fonctions de 2 variables, et voilà l’approche qui me semble la plus économe en terme de notions à introduire (et aussi la plus “naturelle” peut-être).

. L’idée est de commencer par obtenir le plus simplement possible un developpement limité à l’ordre 2 pour une fonction f(x,y).
on part d’un développement limité à l’ordre 2 pour une fonction d’une variable :
on pose g(t) = f(x+th, y+tk)

on calcule g’(t) = lim_{Δt->0} [ f(x + (t+Δt)h , y + (t+Δt)k) - f(x+th, y+tk) ] / Δt
= lim [ f(x + (t+Δt)h , y + (t+Δt)k) - f(x+th, y+ (t+Δt)k )]/(Δt.h) . h +
[ f(x + t h , y + (t+Δt)k) - f(x+th, y + t k )]/(Δt.k) . k
= ∂f/∂x (x+th, y+tk) . h + ∂f/∂y (x+th, y+tk) . k

en procédant de même pour la dérivée seconde (+ schwarz), on obtient :
g”(t) = ∂²f/∂x² (x+th, y+tk) . h² + 2.∂²f/∂x∂y (x+th, y+tk) . hk ∂²f/∂y² (x+th, y+tk) . k²

on écrit le dl de g à l’ordre 2 pour t=1 et t=0
g(1) = g(0) + g’(0) + 1/2 g”(0) + reste

soit en terme de f :
f(x+h, y+k) = f(x,y) + ∂f/∂x (x, y) . h + ∂f/∂y (x, y) . k + 1/2 (∂²f/∂x² (x, y) . h² + 2.∂²f/∂x∂y (x, y) . hk + ∂²f/∂y² (x, y) . k² ) + reste

. passons à la recherche d’extremum :
au niveau d’un point stationnaire le gradient est nul, voir mon petit topo de la dernière fois, ou encore deux façons de le faire sentir :
- on “voit” que le plan tangent est plat comme en 1D la tangente était de pente nulle
- ou plus simple peut-être, au niveau d’un point (x_0,y_0) qui permet l’extremum on fixe par exemple y_0 et on se retrouve avec le cas 1D : si on fait varier localement x, h(x,y_0) a forcément aussi un point critique en x_0, d’où la première dérivée partielle nulle. idem pour la seconde.

le dl obtenu précédemment nous donne alors, dans le cas d’un minimum pour fixer les idées, en négligeant le reste :
∂²f/∂x². h² + 2.∂²f/∂x∂y (x, y) . hk ∂²f/∂y² (x, y) . k² > 0

. il faut alors procéder à l’étude du signe de la forme quadratique : A h² + 2B hk + C k²
on pose λ = h/k, cela revient à l’étude de : A λ² + 2B λ + C
et on obtient le thm de Lagrange en regardant le signe de ce polynôme.

. on peut ensuite introduire les notions de concavité convexité en faisant le parallèle avec ce que l’on sait pour 1 variable.

(L’idée de l’étude du Hessien peut au besoin, dériver de cela comme une généralisation/automatisation)

Artaud, toujours.
Mon premier choc. et s’il n’en reste qu’un, il sera le dernier.
J’ai l’impression d’avoir muri ce passage en moi depuis plus de vingt ans jusqu’à effectivement le rejoindre en conscience.
Fiction fiction, littérature, poésie, je n’en peux toujours plus.

autre Pezner de ma vie par là ->.

Avant d’entrer dans ce batiment-là :

je suis passée devant les ailes de cryptogamie et de phanérogamie ; j’apprends donc qu’il s’agit de l’étude des plantes dont les organes de reproduction sont cachés pour le premier et apparents pour le second.
Un petit zoom au dessous (il suffit aussi de cliquer sur celle au-dessus pour explorer les détails, et non, je n’ai toujours pas honte d’utiliser encore les mêmes filtres putassiers).

Tout cela n’ayant absolument rien à voir avec l’hétérogamie, l’homogamie, l’hypo ou encore l’hypergamie.
À part ça, j’ai écouté Michael Nyman tout l’après-midi, et même Motives for writing de Wim Mertens que je connais encore par coeur, 15 ans après que j’aie définitivement mis mon (gros) lot de cassettes au rebut et auquel mon exemplaire de cet album faisait partie, aux cotés de plein d’autres choses dont une certaine part tout à fait oubliable. Et terminé par un morceau terrible de Ornette Coleman terriblement repris par John Zorn (et compagnie). Bonne nuit.

à chaque fois ça me puzzle, pourtant c’est évident !
le gradient est normal à la courbe de niveau, tout simplement parce que c’est leur raison d’être : la courbe de niveau indique le chemin sur une surface qui permet de rester à valeur constante, le gradient est le vecteur qui indique la variation (et qui plus est, la direction de plus forte variation). - ça c’est pour la philosophie -

si on fait un développement limité, pour X dans Rⁿ, t un réel et v un vecteur de Rⁿ, on a f(x+tv) = f(x) + t∇f(x).v + reste , sur la courbe de niveau on a justement f(x+tv) = f(x) donc ∇f(x) est orthogonal à v, pour tout v tel que x+tv est sur la courbe de niveau - ça c’est pour l’analyse -

mais ce qui me puzzle vraiment, plus précisément, c’est la relation avec le plan tangent, certainement du fait de mon inculture géométrique, j’en ai toujours été très complexée.

les dérivées partielles correspondent séparément à la pente de la tangente le long de la courbe donnée par l’intersection de la surface définie par l’équation de la fonction et du plan obtenu fixant la variable qu’on ne va pas dériver au point considéré. ex : z = f(x,y) pour x₀ et y₀, l’intersection de la surface représentant f et du plan y = y₀ est la courbe donnée par la fonction qui à x associe f(x,y₀), la tangente à cette courbe en x₀ sera donnée par :
z = f(x₀,y₀) + δf⁄δx (x₀,y₀) (x -x₀ )
de même, la tangeante à la courbe de la fonction qui à y associe f(x₀,y) en y₀ sera donnée par :
z = f(x₀,y₀) + δf⁄δy (x₀,y₀) (y -y₀ )
le plan déterminé par les deux tangentes est alors donné par :
z = f(x₀,y₀)+ δ f⁄δx (x₀,y₀) (x -x₀ ) + δ f⁄δ y (x₀,y₀) (y -y₀ )
(ce qui signifie en gros qu’une fonction de R² sera dérivable si ce plan constitue une bonne approximation locale de la fonction, et pas uniquement dans les directions x et y)
de l’équation du plan tangeant, on tire donc son vecteur normal : (δf⁄δx, δf⁄δy, -1) soit ( ∇f(x), -1) .

Par ailleurs, intéressons-nous aux courbes de niveau, c’est à dire, pour a donné, l’ensemble des points du plan (x,y) tels que f(x,y) = a. Le théorème des fonctions implicites nous dit justement que si les dérivées partielles de f existent et sont continues dans un voisinage d’un point (x₀,y₀) de la courbe de niveau a avec la dérivée partielle en y non nulle, on sait qu’il existe des voisinages U de x₀ et V de y₀ et une unique fonction y(x) de U dans V tels que f(x,y(x))=a. De plus, cette fonction y est différentiable et satisfait y’(x) = - δf(x,y(x))⁄δx / δf(x,y(x))⁄δy. Ceci nous donne le vecteur directeur de la tangente à la ligne de niveau en (x₀,y₀) : (1, - δf(x,y(x))⁄δx / δf(x,y(x))⁄δy) *. Par ailleurs la projection sur le plan (x,y) du vecteur normal au plan tangent est donné tout simplement par le gradient (δf(x,y(x))⁄δx , δf(x,y(x))⁄δy), on voit bien qu’il est alors orthogonal à la ligne de niveau ! la boucle est bouclée.

(il n’est bien sûr jamais trop tard pour réaliser aussi qu’en 1D, l’équation de la tangente est donné par y = f’(x₀)(x-x₀) + f(x₀), elle a bien pour vecteur directeur (1,f’(x₀)) et pour vecteur normal (f’(x₀), -1).)
(* oui et donc l’équation de la tangente à la courbe de niveau est bien l’intersection du plan tangent avec le plan (x0y), reporter dans l’équation du plan tangent z=0 )

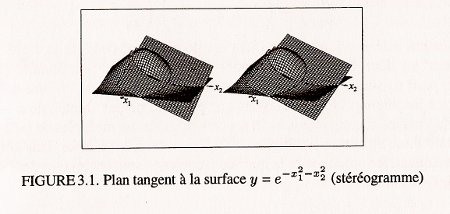
(référence de tout cela et copyright du stéréogramme - quelle bonne idée ! - , -il y en a d’autres dans le livre-, toujours l’excellentissime “Analyse au fil de l’histoire” de E. Hairer et G. Wanner)

Je me sens mieux.