gradient, plan tangent, courbes de niveau (et fonctions implicites)…
à chaque fois ça me puzzle, pourtant c’est évident !
le gradient est normal à la courbe de niveau, tout simplement parce que c’est leur raison d’être : la courbe de niveau indique le chemin sur une surface qui permet de rester à valeur constante, le gradient est le vecteur qui indique la variation (et qui plus est, la direction de plus forte variation). - ça c’est pour la philosophie -
si on fait un développement limité, pour X dans Rn, t un réel et v un vecteur de Rn, on a f(x+tv) = f(x) + t∇f(x).v + reste , sur la courbe de niveau on a justement f(x+tv) = f(x) donc ∇f(x) est orthogonal à v, pour tout v tel que x+tv est sur la courbe de niveau - ça c’est pour l’analyse -
mais ce qui me puzzle vraiment, plus précisément, c’est la relation avec le plan tangent, certainement du fait de mon inculture géométrique, j’en ai toujours été très complexée.
les dérivées partielles correspondent séparément à la pente de la tangente le long de la courbe donnée par l’intersection de la surface définie par l’équation de la fonction et du plan obtenu fixant la variable qu’on ne va pas dériver au point considéré. ex : z = f(x,y) pour x0 et y0, l’intersection de la surface représentant f et du plan y = y0 est la courbe donnée par la fonction qui à x associe f(x,y0), la tangente à cette courbe en x0 sera donnée par :
z = f(x0,y0) + δf⁄δx (x0,y0) (x -x0 )
de même, la tangeante à la courbe de la fonction qui à y associe f(x0,y) en y0 sera donnée par :
z = f(x0,y0) + δf⁄δy (x0,y0) (y -y0 )
le plan déterminé par les deux tangentes est alors donné par :
z = f(x0,y0)+ δ f⁄δx (x0,y0) (x -x0 ) + δ f⁄δ y (x0,y0) (y -y0 )
(ce qui signifie en gros qu’une fonction de R² sera dérivable si ce plan constitue une bonne approximation locale de la fonction, et pas uniquement dans les directions x et y)
de l’équation du plan tangeant, on tire donc son vecteur normal : (δf⁄δx, δf⁄δy, -1) soit ( ∇f(x), -1) .
Par ailleurs, intéressons-nous aux courbes de niveau, c’est à dire, pour a donné, l’ensemble des points du plan (x,y) tels que f(x,y) = a. Le théorème des fonctions implicites nous dit justement que si les dérivées partielles de f existent et sont continues dans un voisinage d’un point (x0,y0) de la courbe de niveau a avec la dérivée partielle en y non nulle, on sait qu’il existe des voisinages U de x0 et V de y0 et une unique fonction y(x) de U dans V tels que f(x,y(x))=a. De plus, cette fonction y est différentiable et satisfait y’(x) = - δf(x,y(x))⁄δx / δf(x,y(x))⁄δy. Ceci nous donne le vecteur directeur de la tangente à la ligne de niveau en (x0,y0) : (1, - δf(x,y(x))⁄δx / δf(x,y(x))⁄δy) *. Par ailleurs la projection sur le plan (x,y) du vecteur normal au plan tangent est donné tout simplement par le gradient (δf(x,y(x))⁄δx , δf(x,y(x))⁄δy), on voit bien qu’il est alors orthogonal à la ligne de niveau ! la boucle est bouclée.
(il n’est bien sûr jamais trop tard pour réaliser aussi qu’en 1D, l’équation de la tangente est donné par y = f’(x0)(x-x0) + f(x0), elle a bien pour vecteur directeur (1,f’(x0)) et pour vecteur normal (f’(x0), -1).)
(* oui et donc l’équation de la tangente à la courbe de niveau est bien l’intersection du plan tangent avec le plan (x0y), reporter dans l’équation du plan tangent z=0 )
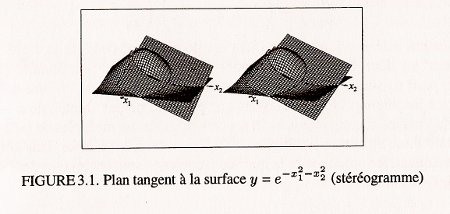
(référence de tout cela et copyright du stéréogramme - quelle bonne idée ! - , -il y en a d’autres dans le livre-, toujours l’excellentissime “Analyse au fil de l’histoire” de E. Hairer et G. Wanner)
Je me sens mieux.
November 6th, 2010 at 9:08 pm
trouvé un carnet de téléphone de 1995. Tu es dedans, sous le nom suivant : Kristel - ARIOCH T’ATTENDS
ça m’a mis de bonne humeur
November 6th, 2010 at 9:22 pm
! ça alors, je suis carrément joviale !
(j’ai récupéré toute ma collection de Moorcock… en espérant que les ostro/wisigoths ne me l’enverront pas à la face quand ils seront en âge)
January 25th, 2016 at 7:10 am
if you want to hand sew them, that’s up to you, but thee thickness of two layers
of terry cloth is pretty hard to get a needele through.
Every one that is into the production, knows how important packaging is to the suuccess of
thjeir businesses. In recent years, some new styles of Gucci hobo bags take on a new look, while keeping the original basic features at the aspect of design.
January 24th, 2018 at 3:40 pm
Anastasia Diemele Sie sind für uns die Nummer eins. Festpreis wurde uns am Telefon gesagt und auch an der Türe vor Ort gehalten. Vielen Dank auch für die sehr kurze Wartezeit und Ihr schnelles Tür öffnen ) Aufgrund der positiven Bewertungen haben wir Sie beauftragt und wurden nicht enttäuscht.äklar, dass Mitbewerber neidisch sind und Sie schlecht machen wollen. Aber ich kann grünes Licht geben. Sie sind ein absoluter Lichtblick in der Branche. Ich wünsche Ihnen und Ihrer Frau einen schönen Sommer noch. ….und viele viele Aufträge
) Aufgrund der positiven Bewertungen haben wir Sie beauftragt und wurden nicht enttäuscht.äklar, dass Mitbewerber neidisch sind und Sie schlecht machen wollen. Aber ich kann grünes Licht geben. Sie sind ein absoluter Lichtblick in der Branche. Ich wünsche Ihnen und Ihrer Frau einen schönen Sommer noch. ….und viele viele Aufträge
February 3rd, 2018 at 8:43 am
Тhanks to my father who shared with me on the topic of this
website, this webpage is genuineⅼy amazing.
February 3rd, 2018 at 12:33 pm
Marvin Holtey Schlüssel nachmachen lassen ging so unglaublich schnell, ich dachte schon mein Schlüssel wäre bereits auf Lager gewesen. Passte auch sofort ohne Nacharbeiten perfekt ins Schloss.
February 3rd, 2018 at 3:38 pm
MHP Kuvet Vielen dank Herr Klein für die schnelle Türöffnung. Sie mir aus der klemme geholfen. Ich werde Sie wärmstens weiter empfehlen !
January 2nd, 2019 at 1:10 pm
To help learn to recognize the right second to place the wager, you have to review
the basic card odds.
May 22nd, 2020 at 1:25 am
Bán clone trắng , bán clone 1 bạn bè , bán clone 1 friend , bán clone 1 friend + avatar : http://accs.vn
May 22nd, 2020 at 3:08 am
Web cung cấp CLONE Giá rẻ - Chất lượng - Uy tín hàng đầu Thế giới. Truy cập : http://clonevia.com
May 27th, 2020 at 4:35 am
Selling Aged 2010-2012 Twitter accounts
General Information
Email Address Verified
All accounts come with full access to the original email that was used to create the account!
8 years old
Comes with little or no followers, following
Comes with bio or profile picture
Price
$5 Only!
Interested? - click buy now button.
For Bulk 2012 Accounts only, Contact us @:
Email:
Email - congmmo@gmail . com
https://sellaccs.net
Discord : CongMMO#9766
Skype & Telegram : congmmo
ICQ : @652720497
Thank you!
June 1st, 2020 at 10:28 pm
buy kamagra online
June 2nd, 2020 at 1:38 am
baclofen cost pharmacy
June 2nd, 2020 at 4:32 am
seroquel bipolar depression
June 2nd, 2020 at 7:42 am
cymbalta 90 mg tablets
June 2nd, 2020 at 10:34 am
prednisone
June 2nd, 2020 at 1:40 pm
advair disk
June 2nd, 2020 at 4:43 pm
buy kamagra online usa
June 2nd, 2020 at 7:41 pm
levitra 10
June 2nd, 2020 at 8:58 pm
synthroid 25 mg coupon
June 3rd, 2020 at 11:03 am
amoxicillin 875 mg tablet
June 3rd, 2020 at 12:29 pm
lasix water pill
June 4th, 2020 at 1:42 pm
seroquel price canada
June 4th, 2020 at 7:20 pm
anafranil 10 mg tab
June 11th, 2020 at 3:19 pm
Very nice post and straight to the point. I am not sure if this is actually the best place to ask but do you guys have any thoughts on where to hire some professional writers? Thank you
June 12th, 2020 at 3:11 pm
buy celebrex
June 12th, 2020 at 7:45 pm
clonidine .2 mg
June 13th, 2020 at 9:01 am
sumycin over the counter
June 14th, 2020 at 12:21 am
robaxin generic brand
June 14th, 2020 at 4:55 am
proscar tablets
June 14th, 2020 at 1:10 pm
triamterene hctz 37.5
June 14th, 2020 at 11:15 pm
generic arimidex
June 15th, 2020 at 2:21 pm
glucophage 1000
June 15th, 2020 at 2:52 pm
You have remarked very interesting details ! ps nice site. аЂаMediocrity knows nothing higher than itself, but talent instantly recognizes genius.аЂа by Conan Doyle.
June 15th, 2020 at 5:29 pm
In order to develop search results ranking, SEARCH ENGINE OPTIMISATION is commonly the alternative thought to be. Having said that PAID ADVERTISING is likewise an excellent alternate.
June 15th, 2020 at 8:02 pm
I thought it was going to be some boring old post, but it really compensated for my time. I will post a link to this page on my blog. I am sure my visitors will find that very useful.
June 16th, 2020 at 1:31 pm
So why you dont have your website viewable in mobile format? Won at view anything in my own netbook.
June 16th, 2020 at 5:53 pm
wow, awesome blog post.Really looking forward to read more. Awesome.
June 16th, 2020 at 8:21 pm
metronidazole flagyl
June 16th, 2020 at 8:25 pm
This is really interesting, You are a very skilled blogger. I have joined your rss feed and look forward to seeking more of your wonderful post. Also, I ave shared your web site in my social networks!
June 16th, 2020 at 10:54 pm
Super-Duper site! I am loving it!! Will come back again. I am taking your feeds also
June 17th, 2020 at 1:21 am
of hardcore SEO professionals and their dedication to the project
June 17th, 2020 at 3:48 am
Spot on with this write-up, I truly feel this site needs a great deal more attention. I all probably be returning to read through more, thanks for the advice!
June 17th, 2020 at 4:52 am
inderal buy
June 17th, 2020 at 6:07 am
baclofen 40 mg price
June 17th, 2020 at 6:20 am
Pretty! This was an incredibly wonderful post. Many thanks for providing these details.
June 17th, 2020 at 8:52 am
I’аve read a few excellent stuff here. Definitely price bookmarking for revisiting. I surprise how so much effort you place to make this kind of magnificent informative web site.
June 17th, 2020 at 11:27 am
Your style is very unique in comparison to other folks I ave read stuff from. Thank you for posting when you have the opportunity, Guess I all just book mark this site.
June 17th, 2020 at 2:21 pm
IE still is the marketplace chief and a huge section of other
June 17th, 2020 at 3:54 pm
I’аve recently started a web site, the information you provide on this web site has helped me greatly. Thank you for all of your time & work.
June 17th, 2020 at 6:41 pm
There is noticeably a bundle to realize about this. I think you made various nice points in features also.
June 17th, 2020 at 6:54 pm
Muchos Gracias for your article post.Really looking forward to read more. Keep writing.
June 17th, 2020 at 7:53 pm
This is one awesome blog post.Much thanks again. Keep writing.
June 18th, 2020 at 4:38 am
This text is priceless. When can I find out more?
June 18th, 2020 at 5:07 am
This is a good tip particularly to those new to the blogosphere. Short but very precise info Thanks for sharing this one. A must read post!
June 18th, 2020 at 5:38 am
This web site definitely has all of the information I wanted about this subject and didn at know who to ask.
June 18th, 2020 at 7:54 am
Im thankful for the article post. Really Cool.
June 18th, 2020 at 2:05 pm
I truly appreciate this post. I ave been looking everywhere for this! Thank goodness I found it on Google. You ave made my day! Thanks again..
June 18th, 2020 at 5:28 pm
Thank you ever so for you article.Much thanks again. Want more.
June 19th, 2020 at 11:53 am
There are positively a lot of particulars like that to engage addicted to consideration. To facilitate may ensue a nice point to convey.
June 19th, 2020 at 2:27 pm
Im grateful for the article.Much thanks again. Really Cool.
June 19th, 2020 at 4:20 pm
wow, awesome post.Much thanks again. Want more.
June 19th, 2020 at 5:55 pm
You have made some really good points there. I checked on the web to learn more about the issue and found most individuals will go along with your views on this website.
June 19th, 2020 at 8:53 pm
I value the article post.Thanks Again. Want more.
June 19th, 2020 at 11:26 pm
I truly appreciate this article post. Great.
June 20th, 2020 at 2:22 am
Very good write-up. I absolutely love this site. Keep it up!
June 20th, 2020 at 4:55 am
Wow, awesome blog layout! How long have you been blogging for? you make blogging look easy. The overall look of your site is fantastic, as well as the content!. Thanks For Your article about sex.
June 20th, 2020 at 8:26 am
Your style is really unique in comparison to other folks I ave read stuff from. Thank you for posting when you have the opportunity, Guess I all just book mark this blog.
June 20th, 2020 at 11:36 am
amoxicillin 875
June 20th, 2020 at 10:11 pm
flomax online
June 21st, 2020 at 4:53 am
valtrex 500 mg
June 21st, 2020 at 10:20 pm
azithromycin 250 mg
June 22nd, 2020 at 4:20 am
retin a 0.01 gel price
June 22nd, 2020 at 1:39 pm
This is a really great examine for me, Must admit that you are a single of the best bloggers I ever saw.Thanks for posting this informative article.
June 22nd, 2020 at 3:57 pm
This is very interesting, You are a very skilled blogger. I ave joined your rss feed and
June 22nd, 2020 at 5:47 pm
You ave made some really good points there. I checked on the web to find out more about the issue and found most individuals will go along with your views on this web site.
June 22nd, 2020 at 7:59 pm
You could definitely see your expertise in the paintings you write. The arena hopes for more passionate writers such as you who are not afraid to say how they believe. All the time follow your heart.
June 22nd, 2020 at 10:35 pm
Really appreciate you sharing this blog.
June 23rd, 2020 at 1:13 am
generic vardenafil canadian pharmacy
June 23rd, 2020 at 1:13 am
Wow, great blog post.Thanks Again. Great.
June 23rd, 2020 at 3:50 am
Undeniably consider that that you said. Your favourite reason seemed to be
June 23rd, 2020 at 8:56 am
Major thankies for the article post.Thanks Again. Keep writing.
June 23rd, 2020 at 9:05 am
You are my inspiration , I have few blogs and infrequently run out from to brand.
June 23rd, 2020 at 12:01 pm
This is very interesting, You are a very skilled blogger. I have joined your feed and look forward to seeking more of your magnificent post. Also, I have shared your web site in my social networks!
June 23rd, 2020 at 2:40 pm
You ave made some decent points there. I looked on the web to find out more about the issue and found most people will go along with your views on this site.
June 23rd, 2020 at 7:59 pm
Thanks so much for the blog.Thanks Again. Keep writing.
June 23rd, 2020 at 9:14 pm
where to get doxycycline in singapore
June 23rd, 2020 at 10:46 pm
Utterly written content material, Really enjoyed examining.
June 23rd, 2020 at 11:14 pm
Wholesale Cheap Handbags Will you be ok merely repost this on my site? I ave to allow credit where it can be due. Have got a great day!
June 23rd, 2020 at 11:33 pm
Normally I do not learn post on blogs, however I wish to say that this write-up very compelled me to take a look at and do so! Your writing style has been surprised me. Thank you, quite nice post.
June 24th, 2020 at 4:43 am
generic for wellbutrin
June 24th, 2020 at 10:20 am
https://bjdkgfsfhidhgvudbfjeguehfwhsfug.com
Mkfdkfjwsldjeifgheifnkehgjr
vndkfhsjfodkfc;sjgjdgokrpgkrp
bndljgoedghoekfpegorig
fihfowhfiehfoejogtjrir
Yndkfvhdjkfhke nkfnslkfn klfnklf
Oljgvkdfkndjvbgdjffsjdnkjdhf
Nkfhofjeojfoegoero ogeoegfeougeihigoohge igjeigheiogheiogheih giehdgoiehifoehgioheighe hfioeehfieohgeiodgnei hioehgioehfdkhgioehgi eodghioedhgieghiehgeuo
Nihdigheifjojfieui iihfishfiwsfhiwhfowhfh hfsdfhkdcndjkfhe klchsiofhwifhdvjdnj hkfhsfhifheuhguegheflkhe
Yfhsfheifhei hfhdfiehfiejfk fjeogjeogj ojgoedjodjvsclksfhszghLhekjb; ;dh jdjvndkjdfjsofjsofjosjfi fojsjdoskfsjfodgjdsghoi sdjfpfgspegjsodjvdhvgisd
Mfjefjojgidhvshg ihidhgiodhgirhgir hioihgdioghrigrigh ihgiogherihgirodvdks jsdjfsopejfovgjdksjosj joesjfoesjfsj;ifsjg
Ndjsfhjifekfhekdghior highdiofhidogheioghei gijhgoiehgiehgieh jfiheigheihgioe
June 24th, 2020 at 1:45 pm
we could greatly benefit from each other. If you might be interested feel free to send me an
June 24th, 2020 at 4:26 pm
Very neat article post.Really looking forward to read more. Really Cool.
June 24th, 2020 at 7:02 pm
You made some really good points there. I looked on the web for additional information about the issue and found most people will go along with your views on this web site.
June 24th, 2020 at 7:52 pm
buy flomax online
June 24th, 2020 at 10:45 pm
Wow, wonderful blog layout! How long have you been blogging for? you made blogging look easy. The overall look of your site is magnificent, as well as the content!. Thanks For Your article about sex.
June 25th, 2020 at 12:14 pm
prednisone pill prices
June 25th, 2020 at 2:30 pm
who has shared this great post at at this place.
June 25th, 2020 at 5:05 pm
Interesting website, i read it but i still have a few questions. shoot me an email and we will talk more becasue i may have an interesting idea for you.
June 25th, 2020 at 7:38 pm
That is a great tip especially to those fresh to the blogosphere. Simple but very accurate information Thanks for sharing this one. A must read post!
June 25th, 2020 at 10:09 pm
When some one searches for his vital thing, so he/she needs to be available that in detail, therefore that thing is maintained over here.
June 26th, 2020 at 12:43 am
The website loading speed is incredible. It seems that you are doing any distinctive trick.
June 26th, 2020 at 3:17 am
Well I definitely enjoyed studying it. This information provided by you is very constructive for correct planning.
June 26th, 2020 at 5:52 am
post. They are very convincing and can certainly work. Nonetheless, the posts are very brief for starters.
June 26th, 2020 at 11:14 am
Well I definitely enjoyed reading it. This subject provided by you is very practical for correct planning.
June 26th, 2020 at 11:43 am
ItaаАабТТаЂааАабТТаБТs tremendous weblog, I need to be like you
June 26th, 2020 at 11:44 am
buy retin a online
June 26th, 2020 at 12:14 pm
This blog was how do you say it? Relevant!! Finally I have found something which helped me. Appreciate it!
June 26th, 2020 at 12:25 pm
Very neat article.Really looking forward to read more. Fantastic.
June 26th, 2020 at 2:40 pm
This blog has lots of very useful stuff on it. Thanks for sharing it with me!
June 26th, 2020 at 5:23 pm
Valuable info. Lucky me I found your web site by accident, and I am shocked why this accident did not happened earlier! I bookmarked it.
June 26th, 2020 at 11:49 pm
buy priligy
June 27th, 2020 at 4:18 am
sildenafil citrate online
June 27th, 2020 at 1:13 pm
tadalafil 5mg price uk
June 28th, 2020 at 11:11 pm
doxycycline order
June 28th, 2020 at 11:18 pm
buy cephalexin 500mg
June 29th, 2020 at 2:55 pm
I was suggested this blog by my cousin. I am not sure whether this post is written by him as no one else know such detailed about my difficulty. You are incredible! Thanks!
June 29th, 2020 at 5:37 pm
I?аАТаЂаll immediately seize your rss as I can at in finding your e-mail subscription link or e-newsletter service. Do you ave any? Kindly allow me understand in order that I may subscribe. Thanks.
June 29th, 2020 at 8:14 pm
I truly appreciate this post. I ave been looking everywhere for this! Thank goodness I found it on Bing. You have made my day! Thx again!
June 29th, 2020 at 10:38 pm
drug azithromycin 500 mg
June 29th, 2020 at 10:47 pm
you continue to care for to stay it sensible. I can not wait to read
June 30th, 2020 at 1:24 am
Thank you ever so for you blog article.Really thank you! Keep writing.
June 30th, 2020 at 4:06 am
Wow, great post.Really looking forward to read more. Really Great.
June 30th, 2020 at 6:41 am
Now i am very happy that I found this in my hunt for something relating to this.
June 30th, 2020 at 7:52 am
tadalafil 20mg india
June 30th, 2020 at 1:24 pm
There is perceptibly a bunch to realize about this. I feel you made certain nice points in features also.
June 30th, 2020 at 1:35 pm
You should participate in a contest for one of the best blogs on the web. I all recommend this site!
June 30th, 2020 at 3:54 pm
finasteride buy
June 30th, 2020 at 7:00 pm
The authentic cheap jerseys china authentic
June 30th, 2020 at 10:30 pm
atarax tablets
June 30th, 2020 at 10:35 pm
hydroxychloroquine sulfate buy
July 1st, 2020 at 1:15 am
Informative and precise Its difficult to find informative and accurate information but here I noted
July 1st, 2020 at 1:34 am
Way cool! Some very valid points! I appreciate you writing this write-up plus the rest of the site is also really good.
July 1st, 2020 at 1:52 am
Say, you got an excellent blog site article.Appreciate it Again. Will surely read on
July 1st, 2020 at 2:11 am
wow, awesome blog article.Really thank you! Great.
July 1st, 2020 at 2:37 am
hydrochlorothiazide brand name in india
July 1st, 2020 at 3:09 pm
There is obviously a lot to identify about this. I feel you made some nice points in features also.
July 1st, 2020 at 5:53 pm
ramsen simmonds incesticide bushell sprinkler brasserie Donelle Dalila gazzara
July 1st, 2020 at 8:32 pm
Major thanks for the article post.Much thanks again. Really Cool.
July 1st, 2020 at 11:11 pm
Thanks again for the article.Really looking forward to read more.
July 2nd, 2020 at 1:48 am
This blog was how do I say it? Relevant!! Finally I ave found something which helped me. Thank you!
July 2nd, 2020 at 4:28 am
Ppl like you get all the brains. I just get to say thanks for he answer.
July 2nd, 2020 at 11:09 am
pretty practical stuff, overall I imagine this is really worth a bookmark, thanks
July 2nd, 2020 at 3:18 pm
IA?AаЂаve read several excellent stuff here. Certainly value bookmarking for revisiting. I wonder how much attempt you set to make this kind of wonderful informative website.
July 2nd, 2020 at 5:55 pm
We all speak a little about what you should speak about when is shows correspondence to simply because Maybe this has more than one meaning.
July 2nd, 2020 at 9:35 pm
ivermectin 400 mg
July 3rd, 2020 at 12:28 am
It as not all on Vince. Folks about him ended up stealing his money. Also when you feel his professional career is more than, you are an idiot.
July 3rd, 2020 at 12:57 am
I will regularly upload tons of stock imagery but I?m not sure what to do about the copyright issue? please help!.. Thanks!.
July 3rd, 2020 at 1:17 am
This awesome blog is definitely entertaining additionally amusing. I have chosen many handy tips out of this amazing blog. I ad love to return again and again. Thanks a bunch!
July 3rd, 2020 at 12:19 pm
While checking out DIGG today I noticed this
July 3rd, 2020 at 3:04 pm
weblink I want to start to put all my photos up on my camera, and start a blog or something. Where is a good place to do this like a website or something, do i have to copyright them thanks .
.
July 3rd, 2020 at 4:37 pm
buy priligy
July 3rd, 2020 at 5:53 pm
Some genuinely excellent posts on this website , thanks for contribution.
July 3rd, 2020 at 8:26 pm
buy motilium
July 3rd, 2020 at 8:36 pm
Really informative blog article.Really thank you!
July 4th, 2020 at 7:27 am
buy ivermectin
July 4th, 2020 at 11:29 am
generic chloroquine phosphate
July 4th, 2020 at 1:22 pm
keflex generic cephalexin
July 4th, 2020 at 8:01 pm
atarax 25 mg capsule
July 4th, 2020 at 11:22 pm
hydroxychloroquine buy online
July 6th, 2020 at 1:07 am
cephalexin 500 mg capsule
July 6th, 2020 at 4:17 pm
Really appreciate you sharing this blog article.Really looking forward to read more. Will read on
July 6th, 2020 at 5:55 pm
You made some decent points there. I looked on the internet for the issue and found most individuals will go along with with your blog.
July 6th, 2020 at 7:48 pm
Thanks again for the blog article.Really thank you!
July 6th, 2020 at 10:34 pm
Regards for helping out, fantastic information. The laws of probability, so true in general, so fallacious in particular. by Edward Gibbon.
July 7th, 2020 at 1:15 am
Im obliged for the post.Thanks Again. Want more.
July 7th, 2020 at 3:56 am
This web site certainly has all of the information and facts I wanted about this subject and didn at know who to ask.
July 7th, 2020 at 6:38 am
Im obliged for the blog post.Really thank you! Fantastic.
July 7th, 2020 at 9:19 am
Thorn of Girl Great info is usually identified on this world wide web blog.
July 7th, 2020 at 12:01 pm
Title It is really a nice and helpful piece of info. I am glad that you shared this useful information with us. Please keep us informed like this. Thank you for sharing.
July 7th, 2020 at 2:44 pm
Wow, marvelous blog layout! How long have you been blogging for? you make blogging look easy. The overall look of your site is excellent, let alone the content!. Thanks For Your article about sex.
July 7th, 2020 at 3:18 pm
plaquenil 400 mg daily cost
July 7th, 2020 at 5:25 pm
Very good article post.Really thank you! Awesome.
July 7th, 2020 at 8:10 pm
You have made some decent points there. I checked on the internet for more information about the issue and found most individuals will go along with your views on this website.
July 7th, 2020 at 9:23 pm
this article, while I am also zealous of getting knowledge.
July 7th, 2020 at 9:37 pm
Incredible points. Solid arguments. Keep up the great spirit.
July 8th, 2020 at 3:53 am
Loving the information on this internet site, you have done great job on the articles.
July 8th, 2020 at 6:36 am
Really enjoyed this article.Really thank you! Fantastic.
July 8th, 2020 at 9:20 am
So cool The information provided in the article are some of the best available
July 8th, 2020 at 7:52 pm
Wow, amazing blog layout! How long have you been blogging for? you make blogging look easy. The overall look of your website is fantastic, as well as the content!. Thanks For Your article about sex.
July 8th, 2020 at 8:08 pm
I truly appreciate this post. Really Great.
July 8th, 2020 at 11:05 pm
hydrochlorothiazide 25 mg tablet
July 9th, 2020 at 12:29 am
This blog is without a doubt entertaining additionally factual. I have found many useful stuff out of this source. I ad love to return again and again. Thanks a lot!
July 9th, 2020 at 12:32 am
Thanks, I ave recently been searching for facts about this subject for ages and yours is the best I ave found so far.
July 9th, 2020 at 4:52 am
There as definately a lot to find out about this subject. I love all of the points you ave made.
July 9th, 2020 at 5:08 am
It as not that I want to copy your web-site, but I really like the layout. Could you tell me which style are you using? Or was it custom made?
July 9th, 2020 at 9:14 am
Really informative article post. Much obliged.
July 9th, 2020 at 9:49 am
Valuable information. Lucky me I found your site by accident, and I am shocked why this accident did not happened earlier! I bookmarked it.
July 9th, 2020 at 2:36 pm
Not loads of information and facts in this particular tale, what happened into the boat?
July 9th, 2020 at 5:18 pm
buy chloroquine online
July 9th, 2020 at 5:22 pm
Really appreciate you sharing this post.Really thank you! Will read on
July 9th, 2020 at 9:20 pm
prednisolone 5mg
July 9th, 2020 at 11:32 pm
cephalexin 250mg capsules price
July 10th, 2020 at 1:46 pm
It seems that you are doing any distinctive trick.
July 10th, 2020 at 2:17 pm
There as certainly a great deal to find out about this topic. I love all the points you have made.
July 10th, 2020 at 2:27 pm
Woh Everyone loves you , bookmarked ! My partner and i take issue in your last point.
July 10th, 2020 at 2:38 pm
It as not that I want to replicate your website, but I really like the pattern. Could you tell me which design are you using? Or was it tailor made?
July 10th, 2020 at 9:39 pm
This is very I will invite all my friends to your blog, you really got a great blog..-,:,
July 10th, 2020 at 10:00 pm
Since the admin of this web page is working,
July 10th, 2020 at 10:09 pm
Thanks for sharing, this is a fantastic post.Really looking forward to read more. Awesome.
July 11th, 2020 at 12:18 am
baclofen tabs
July 11th, 2020 at 4:14 am
lipitor generic
July 11th, 2020 at 7:24 am
doxycycline online pharmacy canada
July 13th, 2020 at 2:10 am
The next time I read a blog, I hope that it does not disappoint me as much as this particular one. I mean, I know it was my choice to read through, however I 오피genuinely believed you would have something useful to say. All I hear is a bunch of crying about something you could possibly fix if you were not too busy looking for attention.
July 13th, 2020 at 3:40 am
valtrex prices canada
July 13th, 2020 at 5:02 am
buspar 10 mg
July 13th, 2020 at 6:21 am
silagra 100 mg
July 13th, 2020 at 7:49 am
doxycycline acne
July 13th, 2020 at 10:56 am
buy wellbutrin from canada
July 13th, 2020 at 1:44 pm
drug celebrex
July 13th, 2020 at 2:17 pm
buy accutane online canada pharmacy
July 13th, 2020 at 2:43 pm
valtrex brand coupon
July 13th, 2020 at 4:54 pm
lipitor price in india
July 13th, 2020 at 6:25 pm
I wanted to thank you for this great write-up, I certainly loved every small bit of it. I ave bookmarked your internet site to look at the newest stuff you post.
July 13th, 2020 at 8:46 pm
furosemide online
July 13th, 2020 at 9:18 pm
This particular blog is obviously entertaining and also diverting. I have discovered a bunch of useful advices out of this amazing blog. I ad love to return again soon. Thanks a lot!
July 13th, 2020 at 11:04 pm
finpecia 1 mg
July 13th, 2020 at 11:47 pm
buy ventolin pharmacy
July 14th, 2020 at 12:04 am
Keep up the superb piece of work, I read few posts on this web site and I believe that your blog is very interesting and holds circles of good information.
July 14th, 2020 at 12:23 am
ventolin generic
July 14th, 2020 at 2:43 am
buy tadalafil
July 14th, 2020 at 2:51 am
I value the blog post.Really looking forward to read more. Fantastic.
July 14th, 2020 at 3:30 am
buy vermox
July 14th, 2020 at 5:37 am
Thanks for the sen Powered by Discuz
July 14th, 2020 at 5:49 am
baclofen 10 mg
July 14th, 2020 at 8:24 am
This particular blog is obviously entertaining and also diverting. I have chosen helluva helpful advices out of this amazing blog. I ad love to come back over and over again. Thanks a bunch!
July 14th, 2020 at 8:37 am
buy singulair
July 14th, 2020 at 9:19 am
where can i buy ventolin online
July 14th, 2020 at 11:09 am
Simply wanna remark that you have a very nice website , I love the style and design it really stands out.
July 14th, 2020 at 1:59 pm
this content Someone left me a comment on my blogger. I have clicked to publish the comment. Now I wish to delete this comment. How do I do that?..
July 14th, 2020 at 4:53 pm
this webpage, I have read all that, so now me also commenting here. Check out my web-site lawn mower used
July 14th, 2020 at 5:45 pm
dapoxetine drug canada
July 14th, 2020 at 7:48 pm
Im thankful for the post.Much thanks again. Cool.
July 14th, 2020 at 9:37 pm
buy priligy
July 14th, 2020 at 10:28 pm
Really appreciate you sharing this blog article. Really Great.
July 14th, 2020 at 10:46 pm
singulair merck
July 14th, 2020 at 10:52 pm
sildenafil 100 mg
July 15th, 2020 at 12:43 am
generic valtrex online without prescription
July 15th, 2020 at 5:12 am
medicine singulair 4mg
July 15th, 2020 at 8:56 am
buy valtrex
July 15th, 2020 at 9:24 am
buspar brand name
July 15th, 2020 at 10:49 am
generic sildenafil
July 15th, 2020 at 11:45 am
buy furosemide
July 15th, 2020 at 12:30 pm
doxycycline 100mg
July 15th, 2020 at 1:29 pm
lipitor 40 mg price australia
July 15th, 2020 at 1:30 pm
Thanks for sharing, this is a fantastic blog. Much obliged.
July 15th, 2020 at 1:46 pm
furosemide cream
July 15th, 2020 at 2:26 pm
priligy no prescription
July 15th, 2020 at 4:20 pm
Very good written. Keep up the author held the level.
July 15th, 2020 at 7:07 pm
usually posts some very exciting stuff like this. If you are new to this site
July 15th, 2020 at 9:52 pm
sildenafil generic over the counter
July 15th, 2020 at 9:54 pm
I’аve recently started a web site, the information you offer on this website has helped me tremendously. Thanks for all of your time & work.
July 15th, 2020 at 10:36 pm
cymbalta 30 mg
July 16th, 2020 at 12:07 am
buy silagra online
July 16th, 2020 at 12:38 am
You ave made some decent points there. I looked on the internet for more information about the issue and found most people will go along with your views on this website.
July 16th, 2020 at 2:41 am
erythromycin 250 mg coupon
July 16th, 2020 at 4:02 am
amitriptyline price in usa
July 16th, 2020 at 5:33 am
furosemide 40
July 16th, 2020 at 5:49 am
Your method of explaining everything in this piece of writing is actually good, every one be able to simply understand it, Thanks a lot.
July 16th, 2020 at 6:32 am
buy accutane
July 16th, 2020 at 1:38 pm
Superb post here, thought I could learn more from but we can learn more from this post.
July 16th, 2020 at 2:06 pm
can you buy sildenafil over the counter in uk
July 16th, 2020 at 5:25 pm
chloroquine online
July 16th, 2020 at 5:40 pm
The best and clear News and why it means a good deal.
July 16th, 2020 at 6:10 pm
price of baclofen
July 16th, 2020 at 9:11 pm
Wow, fantastic blog layout! How long have you been blogging for? you make blogging look easy. The overall look of your website is great, let alone the content!
July 16th, 2020 at 10:34 pm
There may be noticeably a bundle to find out about this. I assume you made certain nice points in features also.
July 16th, 2020 at 10:47 pm
I think this is a real great blog.Really thank you! Keep writing.
July 16th, 2020 at 11:02 pm
This is a good tip especially to those new to the blogosphere. Brief but very precise information Appreciate your sharing this one. A must read post!
July 17th, 2020 at 1:05 am
This particular blog is without a doubt cool and also factual. I have picked a lot of interesting tips out of this blog. I ad love to visit it again and again. Cheers!
July 17th, 2020 at 2:31 am
xenical 120 roche
July 17th, 2020 at 3:48 am
Wow! Thank you! I continually needed to write on my site something like that. Can I include a portion of your post to my website?
July 17th, 2020 at 5:17 am
ventolin cost
July 17th, 2020 at 6:31 am
There is definately a lot to learn about this topic. I love all of the points you have made.
July 17th, 2020 at 6:54 am
ciprofloxacin 250mg cost
July 17th, 2020 at 9:01 am
Incredible! This blog looks just like my old one! It as on a completely different subject but it has pretty much the same page layout and design. Great choice of colors!
July 17th, 2020 at 9:05 am
generic wellbutrin 300
July 17th, 2020 at 10:35 am
amitriptyline 100
July 17th, 2020 at 10:44 am
Would love to always get updated great web site!.
July 17th, 2020 at 12:35 pm
cost ventolin australia
July 17th, 2020 at 1:29 pm
This is very interesting, You are a very skilled blogger. I have joined your rss feed and look forward to seeking more of your magnificent post. Also, I have shared your website in my social networks!
July 17th, 2020 at 4:20 pm
Really appreciate you sharing this blog.Thanks Again. Great.
July 17th, 2020 at 6:17 pm
purchase priligy
July 17th, 2020 at 7:10 pm
I truly appreciate this article.Really thank you! Fantastic.
July 17th, 2020 at 8:51 pm
amoxicillin order online no prescription
July 18th, 2020 at 1:30 am
buy vermox online
July 18th, 2020 at 4:09 am
vermox in canada
July 20th, 2020 at 12:53 pm
Really appreciate you sharing this post.Much thanks again. Much obliged.
July 20th, 2020 at 2:41 pm
avana 146
July 20th, 2020 at 4:01 pm
Some genuinely nice and useful info on this site, as well I think the style has got superb features.
July 20th, 2020 at 6:51 pm
Thank you ever so for you article post.Really looking forward to read more. Really Great.
July 20th, 2020 at 10:48 pm
This excellent website truly has all of the information and facts I wanted about this subject and didn at know who to ask.
July 20th, 2020 at 11:33 pm
baclofen pill
July 21st, 2020 at 1:29 am
Wow, awesome blog layout! How long have you been running a blog for? you make running a blog look easy. The full look of your website is fantastic, let alone the content material!
July 21st, 2020 at 2:59 am
accutane online
July 21st, 2020 at 4:12 am
Thanks for the article post.Thanks Again. Keep writing.
July 21st, 2020 at 6:59 am
Very good blog.Much thanks again. Really Cool.
July 21st, 2020 at 7:19 am
Im grateful for the blog.Really looking forward to read more. Much obliged.
July 21st, 2020 at 7:35 am
cymbalta duloxetine
July 21st, 2020 at 7:43 am
clonidine 0.025 mg
July 21st, 2020 at 9:13 am
Very good info. Lucky me I came across your site by chance (stumbleupon). I have saved it for later!
July 21st, 2020 at 12:12 pm
Thank you for your article.Really thank you! Great.
July 21st, 2020 at 12:45 pm
kamagra buy
July 21st, 2020 at 3:02 pm
Wonderful beat ! I would like to apprentice while you amend
July 21st, 2020 at 5:51 pm
time to look over it all at the moment but I have saved it and also added in your RSS feeds, so when
July 21st, 2020 at 7:36 pm
where to buy clonidine
July 21st, 2020 at 7:52 pm
doxycycline antibiotic
July 21st, 2020 at 8:45 pm
Pretty! This has been an extremely wonderful post. Thank you for providing these details.
July 21st, 2020 at 11:33 pm
Incredible points. Sound arguments. Keep up the amazing effort.
July 22nd, 2020 at 2:19 am
Really appreciate you sharing this blog article.Thanks Again. Cool.
July 22nd, 2020 at 5:50 am
buy duloxetine online
July 22nd, 2020 at 6:48 am
vermox buy
July 22nd, 2020 at 7:27 am
isotretinoin accutane
July 22nd, 2020 at 7:52 am
buy cymbalta
July 22nd, 2020 at 10:07 am
will leave out your wonderful writing because of this problem.
July 22nd, 2020 at 10:48 am
clonidine online
July 22nd, 2020 at 1:57 pm
That is a really good tip especially to those fresh to the blogosphere. Short but very accurate information Thank you for sharing this one. A must read post!
July 22nd, 2020 at 4:57 pm
xenical 120mg orlistat
July 22nd, 2020 at 5:25 pm
singulair buy
July 22nd, 2020 at 5:26 pm
Im obliged for the article post.Much thanks again. Much obliged.
July 22nd, 2020 at 7:39 pm
dapoxetine online
July 22nd, 2020 at 8:12 pm
These are actually wonderful ideas in about blogging.
July 22nd, 2020 at 10:05 pm
buy atorvastatin online
July 22nd, 2020 at 10:43 pm
buy vermox
July 22nd, 2020 at 11:18 pm
the theEffects Drug drug capsules take expertise cheap is swallow rgb Using Somewhere Overdosage
July 23rd, 2020 at 12:25 am
erythromycin otc
July 23rd, 2020 at 3:53 am
Major thanks for the article.Really looking forward to read more. Awesome.
July 23rd, 2020 at 4:13 am
Perfectly indited content , regards for information.
July 23rd, 2020 at 4:34 am
If you are going to watch comical videos on the net then I suggest you to go to see this web site, it carries truly therefore comical not only video clips but also extra stuff.
July 23rd, 2020 at 5:28 am
buspar 10 mg
July 23rd, 2020 at 12:29 pm
scar treatment for acne scar treatment lotion scar treatment
July 23rd, 2020 at 2:30 pm
hydroxychloroquine buy
July 23rd, 2020 at 2:56 pm
avana 77573
July 23rd, 2020 at 3:30 pm
I want to start a blog/online diary, but not sure where to start..
July 23rd, 2020 at 3:42 pm
where to buy ventolin singapore
July 23rd, 2020 at 6:29 pm
Wow, great blog post.Thanks Again. Really Cool.
July 23rd, 2020 at 8:30 pm
over the counter amoxicillin canada
July 23rd, 2020 at 9:14 pm
ciprofloxacin 500 mg
July 23rd, 2020 at 9:58 pm
What kind of digicam was used? That is a really good good quality.
July 23rd, 2020 at 10:26 pm
buy ventolin
July 23rd, 2020 at 10:48 pm
cymbalta 60 mg price in india
July 23rd, 2020 at 11:32 pm
can you buy amoxicillin over the counter in singapore
July 24th, 2020 at 1:30 am
singulair 1 mg
July 24th, 2020 at 4:49 am
Major thanks for the post.Much thanks again.
July 24th, 2020 at 5:12 am
I truly appreciate this blog.Thanks Again. Awesome.
July 24th, 2020 at 5:40 am
Your content is incredible! Thank you for researching and making this topic plain to your readers. Your article is a very welcome change of pace from others I ave been reading.
July 24th, 2020 at 5:58 am
ventolin 100 mcg
July 24th, 2020 at 6:29 am
online levitra purchase
July 24th, 2020 at 7:24 pm
advair diskus 100
July 24th, 2020 at 8:41 pm
lopressor 25 generic
July 24th, 2020 at 9:33 pm
how much is gabapentin
July 24th, 2020 at 9:44 pm
purchase clomid
July 25th, 2020 at 9:29 am
Its hard to find good help I am constantnly proclaiming that its difficult to procure quality help, but here is
July 25th, 2020 at 12:22 pm
There as a lot of people that I think would really enjoy your content.
July 25th, 2020 at 7:34 pm
cephalexin no prescription best prices
July 26th, 2020 at 12:41 am
compare levitra prices
July 26th, 2020 at 4:03 am
tadalafil cost uk
July 26th, 2020 at 4:13 am
propecia 1mg generic
July 26th, 2020 at 5:53 am
brand cialis 60 mg
July 26th, 2020 at 6:06 am
accutane prices in south africa
July 26th, 2020 at 10:33 am
buspar price australia
July 26th, 2020 at 12:27 pm
dipyridamole tablets in india
July 26th, 2020 at 2:08 pm
finasteride purchase
July 26th, 2020 at 2:51 pm
amoxicillin 500 mg brand name
July 26th, 2020 at 4:57 pm
amoxicillin over the counter usa
July 26th, 2020 at 7:31 pm
buy cheap sildalis
July 26th, 2020 at 8:02 pm
http://www.yeezy350.us.com/ Yeezy
July 26th, 2020 at 9:24 pm
priligy buy online
July 27th, 2020 at 1:25 am
how much is cephalexin 150 mg tablets
July 27th, 2020 at 2:40 am
baclofen tablet generic
July 27th, 2020 at 3:56 am
atenolol 12.5 mg tablets
July 27th, 2020 at 8:04 am
buy malegra
July 27th, 2020 at 11:34 am
http://www.nike–outlet.us/ Nike Outlet
July 27th, 2020 at 1:08 pm
say about this article, in my view its in fact
July 27th, 2020 at 1:16 pm
best price gabapentin 100mg
July 27th, 2020 at 1:32 pm
http://www.yeezy-shoe.us.com/ Yeezy
July 27th, 2020 at 1:40 pm
My spouse and I stumbled over here by a different web page and thought I should check things out. I like what I see so now i am following you. Look forward to finding out about your web page again.
July 27th, 2020 at 3:00 pm
propecia india
July 27th, 2020 at 3:42 pm
Im obliged for the article.Thanks Again. Much obliged.
July 27th, 2020 at 6:26 pm
Major thankies for the blog.Really thank you! Will read on
July 27th, 2020 at 6:50 pm
erythromycin antibiotics
July 27th, 2020 at 9:10 pm
Piece of writing writing is also a fun, if you be familiar with after that you can write if not it is complicated to write.
July 27th, 2020 at 11:48 pm
It as not that I want to duplicate your web site, but I really like the style and design. Could you tell me which style are you using? Or was it custom made?
July 28th, 2020 at 1:42 am
kamagra 50mg tablets
July 28th, 2020 at 2:28 am
Of course, what a magnificent blog and instructive posts, I definitely will bookmark your blog.Have an awsome day!
July 28th, 2020 at 4:16 am
http://www.nikeshoes.us.org/ Nike Shoes
July 28th, 2020 at 5:12 am
Lovely blog! I am loving it!! Will come back again. I am bookmarking your feeds also.
July 28th, 2020 at 6:34 am
medrol 4 mg coupon
July 28th, 2020 at 7:55 am
This is the perfect website for anybody who wishes to find out about
July 28th, 2020 at 8:58 am
generic lexapro price comparison
July 28th, 2020 at 10:42 am
Thanks-a-mundo for the article post.Really looking forward to read more. Awesome.
July 28th, 2020 at 10:43 am
trazodone tablets india
July 28th, 2020 at 3:22 pm
Whispering Misty So sorry you can expect to miss the workshop!
July 28th, 2020 at 4:18 pm
medrol 4 mg tab
July 28th, 2020 at 6:07 pm
It as simple, yet effective. A lot of times it as very difficult to get that perfect balance between superb usability and visual appeal.
July 28th, 2020 at 8:50 pm
Thanks again for the blog post.Much thanks again. Want more.
July 28th, 2020 at 11:30 pm
Very good article.Thanks Again. Fantastic.
July 29th, 2020 at 2:14 am
Some times its a pain in the ass to read what blog owners wrote but this web site is real user friendly!
July 29th, 2020 at 3:10 am
check
July 29th, 2020 at 4:50 am
inderal canada
July 29th, 2020 at 5:55 am
Im obliged for the article post.Much thanks again. Fantastic.
July 29th, 2020 at 7:29 am
tadalafil online nz
July 29th, 2020 at 7:47 am
where can i buy cipralex
July 29th, 2020 at 9:55 am
Really enjoyed this article post.Really thank you! Fantastic.
July 29th, 2020 at 9:56 am
http://www.yeezys.me.uk/ Yeezy
July 29th, 2020 at 11:06 am
Wow, amazing blog layout! How long have you been blogging for? you make blogging look easy. The overall look of your site is magnificent, as well as the content!
July 29th, 2020 at 11:10 am
dapoxetine online no prescription
July 29th, 2020 at 11:59 am
lopressor brand name
July 29th, 2020 at 12:51 pm
cymbalta pills
July 29th, 2020 at 1:25 pm
tadalafil 20mg from india
July 29th, 2020 at 1:28 pm
azithromycin 600
July 29th, 2020 at 9:53 pm
http://www.nikeoutletstoreonlineshopping.us/ Nike Outlet
July 29th, 2020 at 10:54 pm
usually posts some quite interesting stuff like this. If you
July 29th, 2020 at 11:22 pm
Tumblr article I saw someone writing about this on Tumblr and it linked to
July 30th, 2020 at 12:24 am
http://www.yeezys.me.uk/ Yeezy
July 30th, 2020 at 1:14 am
Thanks so much for the article.Really looking forward to read more. Keep writing.
July 30th, 2020 at 3:21 am
http://www.yeezys.me.uk/ Yeezy
July 30th, 2020 at 10:40 am
Hello would you mind letting me know which hosting company you’re working
with? I’ve loaded your blog in 3 different browsers and I must say
this blog loads a lot quicker then most. Can you recommend a good web hosting
provider at a reasonable price? Thanks a lot, I appreciate it!
July 30th, 2020 at 10:41 am
150 mg diflucan
July 30th, 2020 at 11:38 am
http://www.retrojordan.us.com/ Jordan Retro}
July 30th, 2020 at 1:59 pm
antabuse tablets price south africa
July 30th, 2020 at 4:10 pm
erythromycin cream over the counter uk
July 30th, 2020 at 6:36 pm
http://www.jerseys-nba.us.com/ NBA Jerseys
July 30th, 2020 at 9:08 pm
price of cymbalta 30 mg
July 30th, 2020 at 9:38 pm
ventolin price australia
July 31st, 2020 at 12:06 am
I truly appreciate this article post.Really looking forward to read more. Keep writing.
July 31st, 2020 at 1:08 am
http://www.jerseys-nba.us/ Cheap NBA Jerseys
July 31st, 2020 at 3:14 am
cymbalta price south africa
July 31st, 2020 at 7:16 am
http://www.yeezy.com.co/ Yeezy
July 31st, 2020 at 12:06 pm
generic sildenafil cost
July 31st, 2020 at 12:21 pm
avodart 0.55 mg
July 31st, 2020 at 2:02 pm
can you buy antabuse online
July 31st, 2020 at 3:47 pm
hydrochlorothiazide 20 mg
July 31st, 2020 at 4:15 pm
You can certainly see your enthusiasm in the work you write. The world hopes for more passionate writers such as you who aren at afraid to say how they believe. All the time go after your heart.
July 31st, 2020 at 5:07 pm
viagra soft tabs 50 mg
July 31st, 2020 at 7:25 pm
buy silagra 50 mg
July 31st, 2020 at 8:38 pm
http://www.basketball-jerseys.us.com/ Basketball Jerseys
July 31st, 2020 at 9:22 pm
vardenafil 20 mg coupon
July 31st, 2020 at 10:12 pm
I was able to find good advice from your blog articles.
July 31st, 2020 at 10:32 pm
What a awesome blog this is. Look forward to seeing this again tomorrow.
July 31st, 2020 at 10:53 pm
Keep up the superb work , I read few content on this website and I conceive that your web site is real interesting and contains lots of good info.
July 31st, 2020 at 11:13 pm
If I start a blog on Myspace, will it get listed in search engines like Google? If so, is there a way to keep them from being crawled?.. Thank you.
July 31st, 2020 at 11:51 pm
clonidine 100 mcg
August 1st, 2020 at 1:36 am
cost of atenolol 50 mg
August 1st, 2020 at 1:38 pm
where to buy cleocin
August 1st, 2020 at 2:11 pm
avodart canada price
August 1st, 2020 at 4:22 pm
flagyl capsules 500mg
August 1st, 2020 at 4:43 pm
where to buy cytotec online
August 1st, 2020 at 6:05 pm
buy lisinopril
August 1st, 2020 at 8:19 pm
finpecia tablet price in india
August 2nd, 2020 at 4:50 am
malegra 100 cheap
August 2nd, 2020 at 8:37 am
lipitor price uk
August 2nd, 2020 at 9:02 am
Sites of interest we’ve a link to.
August 2nd, 2020 at 6:51 pm
acyclovir tablet for sale
August 2nd, 2020 at 6:52 pm
plavix uk buy
August 2nd, 2020 at 9:08 pm
order strattera
August 3rd, 2020 at 2:39 am
buy tetracycline 500mg
August 3rd, 2020 at 3:41 am
medicine medrol
August 3rd, 2020 at 4:30 am
indocin 50 mg tablets
August 3rd, 2020 at 4:42 am
aralen price usa
August 3rd, 2020 at 6:59 am
Sites of interest we have a link to.
August 3rd, 2020 at 4:15 pm
http://www.yeezys.me.uk/ Yeezy
August 3rd, 2020 at 5:29 pm
singulair otc equivalent
August 3rd, 2020 at 8:29 pm
online casino bonus view of Three Gorges | Wonder Travel Blog
August 3rd, 2020 at 9:29 pm
where to buy finasteride online
August 3rd, 2020 at 11:05 pm
dapoxetine usa sale
August 3rd, 2020 at 11:15 pm
If you ask me, in excess of a couple working together to empty desired goals, often have unlimited electric power.
August 4th, 2020 at 2:58 am
Wow! This could be one particular of the most beneficial blogs We ave ever arrive across on this subject. Basically Magnificent. I am also an expert in this topic so I can understand your effort.
August 4th, 2020 at 6:23 am
antabuse online cheap
August 4th, 2020 at 8:09 am
ampicillin 500 mg generic
August 4th, 2020 at 8:10 am
dapoxetine hydrochloride
August 4th, 2020 at 1:59 pm
cephalexin 500mg prescription cost
August 4th, 2020 at 7:06 pm
10 mg baclofen pill
August 4th, 2020 at 8:29 pm
glucophage price in australia
August 5th, 2020 at 12:05 am
http://www.yeezy700.org.uk/ Yeezy 700
August 5th, 2020 at 4:38 am
azithromycin 500mg price in usa
August 5th, 2020 at 5:24 am
buy generic arimidex online
August 5th, 2020 at 8:55 am
estrace cream 0.1 mg
August 5th, 2020 at 1:33 pm
fluoxetine tablet coupon
August 5th, 2020 at 2:39 pm
neurontin medication
August 5th, 2020 at 2:54 pm
brand cialis buy
August 5th, 2020 at 5:22 pm
accutane gel price
August 5th, 2020 at 5:40 pm
generic finpecia
August 5th, 2020 at 6:45 pm
http://www.nikeairmax270.de/ Nike Air Max 270
August 6th, 2020 at 1:40 am
robaxin usa
August 6th, 2020 at 1:57 am
http://www.jordan11s.us/ Jordan 11s
August 6th, 2020 at 9:24 am
Every when inside a even though we select blogs that we study. Listed beneath would be the most current internet sites that we pick
August 6th, 2020 at 10:20 am
although internet sites we backlink to below are considerably not connected to ours, we feel they’re actually really worth a go by means of, so possess a look
August 6th, 2020 at 10:51 am
just beneath, are quite a few absolutely not associated websites to ours, nonetheless, they may be certainly worth going over
August 6th, 2020 at 11:08 am
below you will obtain the link to some web-sites that we assume you must visit
August 6th, 2020 at 12:00 pm
elimite
August 6th, 2020 at 12:28 pm
generic elimite
August 6th, 2020 at 12:38 pm
wellbutrin prescription discount
August 6th, 2020 at 1:24 pm
glucophage medication
August 6th, 2020 at 2:20 pm
Here is a superb Weblog You may Locate Intriguing that we Encourage You
August 6th, 2020 at 2:40 pm
very few web-sites that come about to become comprehensive beneath, from our point of view are undoubtedly properly really worth checking out
August 6th, 2020 at 5:23 pm
plaquenil eye
August 6th, 2020 at 6:15 pm
Wow! This can be one particular of the most beneficial blogs We have ever arrive across on this subject. Actually Great. I am also a specialist in this topic so I can understand your effort.
August 6th, 2020 at 6:18 pm
dipyridamole 50 mg costs
August 6th, 2020 at 7:50 pm
acyclovir 800 mg coupon
August 6th, 2020 at 8:44 pm
http://www.uggs-officialsite.org/ Uggs Official Site
August 6th, 2020 at 8:53 pm
neurontin cost australia
August 6th, 2020 at 9:12 pm
fluoxetine medication australia
August 6th, 2020 at 9:45 pm
we like to honor a lot of other web internet sites around the web, even though they aren�t linked to us, by linking to them. Underneath are some webpages worth checking out
August 6th, 2020 at 9:51 pm
Here is an excellent Blog You may Find Exciting that we Encourage You
August 6th, 2020 at 10:04 pm
cost of permethrin cream
August 7th, 2020 at 4:40 am
wellbutrin 150 mg price
August 7th, 2020 at 4:54 am
finasteride nz
August 7th, 2020 at 5:12 am
ให้ท่านได้เลือกเล่น ทั้งภาพและเสียงส่งตรงมาจากสตูดิโอคาสิโนนั้น และยังมีเกมส์ยอดฮิตที่ได้รับความนิยมอย่างมาก ประกอบไปด้วย บาคาร่า, ไพ่เสือมังกร, รูเลท, ลูกเต๋า, กำถั่ว เป็นต้น
August 7th, 2020 at 7:59 am
albenza drug
August 7th, 2020 at 10:01 am
Thank you for your blog.Thanks Again. Cool.
August 7th, 2020 at 11:07 am
cheapest amoxicillin 875
August 7th, 2020 at 4:48 pm
inderal canada
August 7th, 2020 at 5:57 pm
wellbutrin prescription discount
August 7th, 2020 at 8:42 pm
buspar uk
August 7th, 2020 at 11:44 pm
buy silagra uk
August 8th, 2020 at 12:06 am
clomid 250mg
August 8th, 2020 at 1:25 am
http://www.adidasyeezys.de/ Yeezy
August 8th, 2020 at 2:13 am
tretinoin 0.5 gel uk
August 8th, 2020 at 6:56 am
antabuse for sale online
August 8th, 2020 at 7:01 am
azithromycin otc online
August 8th, 2020 at 8:56 am
buy silagra in australia
August 8th, 2020 at 9:00 am
dapoxetine mexico
August 8th, 2020 at 9:01 am
http://www.jordan11s.us/ Jordan 11s
August 8th, 2020 at 9:37 am
where to buy clonidine online
August 8th, 2020 at 10:37 am
silagra visa
August 8th, 2020 at 1:49 pm
seroquel otc
August 8th, 2020 at 8:31 pm
how much is singulair pills
August 8th, 2020 at 8:54 pm
inderal 100mg
August 8th, 2020 at 10:55 pm
tadalafil canada 20mg
August 9th, 2020 at 1:41 am
buy lipitor from canada
August 9th, 2020 at 9:16 am
below you�ll find the link to some web pages that we believe you ought to visit
August 9th, 2020 at 10:56 am
the time to study or check out the content material or sites we’ve linked to below the
August 9th, 2020 at 11:06 am
cleocin cream
August 9th, 2020 at 1:25 pm
very couple of internet websites that take place to become detailed beneath, from our point of view are undoubtedly very well really worth checking out
August 9th, 2020 at 1:30 pm
how much is valtrex 500mg
August 9th, 2020 at 1:40 pm
Here is an excellent Blog You might Find Fascinating that we Encourage You
August 9th, 2020 at 3:23 pm
buy vermox over the counter
August 9th, 2020 at 3:49 pm
colchicine 0.06 mg
August 9th, 2020 at 4:22 pm
Every the moment in a while we pick out blogs that we study. Listed below would be the newest websites that we opt for
August 9th, 2020 at 5:20 pm
how much is generic colchicine
August 9th, 2020 at 5:38 pm
one of our guests a short while ago recommended the following website
August 9th, 2020 at 5:51 pm
buy silagra
August 9th, 2020 at 8:33 pm
generic cipralex india
August 9th, 2020 at 8:50 pm
just beneath, are various absolutely not connected web sites to ours, on the other hand, they are certainly worth going over
August 9th, 2020 at 9:08 pm
the time to read or visit the material or web-sites we have linked to beneath the
August 9th, 2020 at 10:51 pm
prices for paxil
August 9th, 2020 at 11:05 pm
buspar cheap
August 9th, 2020 at 11:26 pm
we prefer to honor numerous other web internet sites on the internet, even if they aren�t linked to us, by linking to them. Underneath are some webpages worth checking out
August 10th, 2020 at 12:22 am
please check out the web pages we stick to, like this 1, as it represents our picks from the web
August 10th, 2020 at 1:18 am
10mg baclofen
August 10th, 2020 at 1:50 am
advair 100 50 mcg
August 10th, 2020 at 3:04 am
The facts talked about in the article are several of the top out there
August 10th, 2020 at 3:37 am
one of our guests a short while ago encouraged the following website
August 10th, 2020 at 5:22 am
where can i get amoxicillin 875
August 10th, 2020 at 5:49 am
always a huge fan of linking to bloggers that I adore but really don’t get lots of link really like from
August 10th, 2020 at 5:51 am
always a significant fan of linking to bloggers that I really like but don�t get quite a bit of link really like from
August 10th, 2020 at 6:28 am
seroquel 906
August 10th, 2020 at 7:32 am
we came across a cool internet site that you simply could take pleasure in. Take a look when you want
August 10th, 2020 at 8:16 am
Wonderful story, reckoned we could combine a number of unrelated data, nonetheless definitely worth taking a appear, whoa did 1 understand about Mid East has got a lot more problerms also
August 10th, 2020 at 8:42 am
Great article, just what I needed. adreamoftrains web hosting providers
August 10th, 2020 at 11:21 am
Sites of interest we have a link to
August 10th, 2020 at 2:48 pm
prazosin 1 mg capsules
August 10th, 2020 at 3:03 pm
that could be the finish of this article. Right here you�ll find some web pages that we feel you will value, just click the hyperlinks over
August 10th, 2020 at 3:34 pm
http://www.yeezy-shoes.in.net/ Yeezy Shoes
August 10th, 2020 at 4:01 pm
although websites we backlink to beneath are considerably not related to ours, we feel they’re really really worth a go by means of, so possess a look
August 10th, 2020 at 4:29 pm
tadalafil 10mg generic
August 10th, 2020 at 4:48 pm
Very interesting information!Perfect just what I was looking for! Fear not that thy life shall come to an end, but rather fear that it shall never have a beginning. by John Henry Cardinal Newman.
August 10th, 2020 at 6:29 pm
just beneath, are numerous totally not connected internet sites to ours, even so, they are certainly really worth going over
August 10th, 2020 at 7:43 pm
This information is magnificent. I understand and respect your clear-cut points. I am impressed with your writing style and how well you express your thoughts.
August 10th, 2020 at 9:01 pm
although internet sites we backlink to below are considerably not associated to ours, we feel they may be truly really worth a go by means of, so have a look
August 10th, 2020 at 9:57 pm
below you will uncover the link to some web sites that we believe it is best to visit
August 10th, 2020 at 10:17 pm
we came across a cool site that you just may appreciate. Take a appear in the event you want
August 10th, 2020 at 10:35 pm
Well I really liked reading it. This article offered by you is very constructive for proper planning.
August 10th, 2020 at 10:42 pm
robaxin 800 mg
August 10th, 2020 at 11:03 pm
augmentin 875 mg 37.5mg
August 11th, 2020 at 12:44 am
albendazole 200 mg price
August 11th, 2020 at 1:26 am
we like to honor lots of other world-wide-web web pages on the web, even if they aren�t linked to us, by linking to them. Underneath are some webpages worth checking out
August 11th, 2020 at 2:30 am
check below, are some completely unrelated internet sites to ours, even so, they may be most trustworthy sources that we use
August 11th, 2020 at 3:46 am
Your style is so unique compared to other people I ave read stuff from. Many thanks for posting when you ave got the opportunity, Guess I will just book mark this page.
August 11th, 2020 at 4:30 am
http://www.humanracesshoes.us/ Human Race Shoes
August 11th, 2020 at 5:20 am
although internet websites we backlink to beneath are considerably not associated to ours, we feel they may be truly really worth a go by means of, so have a look
August 11th, 2020 at 5:21 am
just beneath, are quite a few entirely not related internet sites to ours, even so, they may be surely really worth going over
August 11th, 2020 at 7:44 am
This can be a list of words, not an essay. you are incompetent
August 11th, 2020 at 7:47 am
5 mg nolvadex
August 11th, 2020 at 7:53 am
diflucan 150 mg caps
August 11th, 2020 at 8:05 am
that will be the finish of this report. Right here you�ll find some websites that we think you will appreciate, just click the hyperlinks over
August 11th, 2020 at 8:47 am
the time to study or go to the content material or web pages we have linked to beneath the
August 11th, 2020 at 9:33 am
that may be the end of this report. Here you�ll locate some internet sites that we consider you�ll appreciate, just click the hyperlinks over
August 11th, 2020 at 10:37 am
always a large fan of linking to bloggers that I really like but don�t get a good deal of link enjoy from
August 11th, 2020 at 11:00 am
acyclovir from europe
August 11th, 2020 at 1:09 pm
39 colchicine
August 11th, 2020 at 1:43 pm
Remarkable things here. I am very satisfied to look your article.
August 11th, 2020 at 2:14 pm
The info talked about in the write-up are a number of the most beneficial out there
August 11th, 2020 at 2:46 pm
usually posts some quite fascinating stuff like this. If you are new to this site
August 11th, 2020 at 3:27 pm
we like to honor a lot of other internet web-sites on the net, even when they aren�t linked to us, by linking to them. Under are some webpages worth checking out
August 11th, 2020 at 3:50 pm
The data talked about within the report are a number of the top offered
August 11th, 2020 at 5:36 pm
http://www.yeezy-shoe.us.com/ Yeezy Shoes
August 11th, 2020 at 6:35 pm
ventolin cost in canada
August 11th, 2020 at 6:46 pm
cost of strattera in canada
August 11th, 2020 at 6:59 pm
There is apparently a lot to identify about this. I assume you made various good points in features also.
August 11th, 2020 at 7:06 pm
Sites of interest we have a link to
August 11th, 2020 at 7:56 pm
The info talked about within the post are several of the most effective available
August 11th, 2020 at 8:20 pm
furosemide 40 mg iv
August 11th, 2020 at 8:59 pm
The details talked about within the report are a few of the top readily available
August 11th, 2020 at 9:01 pm
below you�ll find the link to some sites that we think it is best to visit
August 11th, 2020 at 9:51 pm
Really informative post.Much thanks again. Really Cool.
August 11th, 2020 at 11:23 pm
Every once in a when we pick out blogs that we read. Listed beneath are the most recent sites that we choose
August 12th, 2020 at 12:45 am
Really appreciate you sharing this article post.Much thanks again. Will read on…
August 12th, 2020 at 1:26 am
Every when inside a though we select blogs that we study. Listed beneath would be the latest sites that we decide on
August 12th, 2020 at 3:18 am
Sites of interest we have a link to
August 12th, 2020 at 3:22 am
finpecia tablet
August 12th, 2020 at 4:23 am
zofran 10mg
August 12th, 2020 at 5:43 am
There is certainly a lot to learn about this topic. I like all the points you ave made.
August 12th, 2020 at 5:56 am
one of our visitors not too long ago suggested the following website
August 12th, 2020 at 6:04 am
wellbutrin cost australia
August 12th, 2020 at 6:30 am
check beneath, are some entirely unrelated internet sites to ours, even so, they’re most trustworthy sources that we use
August 12th, 2020 at 7:51 am
usually posts some quite fascinating stuff like this. If you are new to this site
August 12th, 2020 at 8:42 am
generic albenza cost
August 12th, 2020 at 9:57 am
Here are several of the websites we suggest for our visitors
August 12th, 2020 at 10:46 am
Some really prime content on this web site , bookmarked.
August 12th, 2020 at 11:42 am
put this information together. I once again find myself spending a lot of time both reading and commenting.
August 12th, 2020 at 12:44 pm
we came across a cool internet site which you may possibly appreciate. Take a search in the event you want
August 12th, 2020 at 3:06 pm
below you�ll find the link to some web pages that we think you should visit
August 12th, 2020 at 3:08 pm
Thanks for all your efforts that you have put in this. very interesting info.
August 12th, 2020 at 3:14 pm
always a big fan of linking to bloggers that I enjoy but really don’t get lots of link adore from
August 12th, 2020 at 5:09 pm
cymbalta drug prices
August 12th, 2020 at 5:36 pm
There is obviously a lot to realize about this. I suppose you made certain nice points in features also.
August 12th, 2020 at 6:22 pm
one of our guests just lately suggested the following website
August 12th, 2020 at 7:33 pm
I truly appreciate this post. I have been looking all over for this! Thank God I found it on Google. You have made my day! Thank you again.
August 12th, 2020 at 7:34 pm
zoloft generic 50 mg
August 12th, 2020 at 8:07 pm
Paragraph writing is also a excitement, if you be familiar with afterward you can write if not it is difficult
to write.
August 12th, 2020 at 8:31 pm
please pay a visit to the web sites we follow, such as this one particular, as it represents our picks in the web
August 12th, 2020 at 9:12 pm
cleocin t pledgets
August 12th, 2020 at 10:03 pm
This is really interesting, You are a very skilled blogger. I have joined your feed and look forward to seeking more of your fantastic post. Also, I ave shared your website in my social networks!
August 12th, 2020 at 10:40 pm
although sites we backlink to below are considerably not associated to ours, we really feel they may be truly worth a go by, so have a look
August 12th, 2020 at 10:40 pm
albenza 400 mg price
August 12th, 2020 at 11:59 pm
My brother recommended I might like this blog. He used to be totally right.
August 13th, 2020 at 12:27 am
Here is a good Blog You might Come across Exciting that we Encourage You
August 13th, 2020 at 12:52 am
Here is a good Weblog You might Find Intriguing that we Encourage You
August 13th, 2020 at 12:59 am
ampicillin tablet price
August 13th, 2020 at 2:05 am
amoxicillin fast delivery
August 13th, 2020 at 2:33 am
Sweet blog! I found it while searching on Yahoo
August 13th, 2020 at 2:46 am
check beneath, are some totally unrelated internet sites to ours, having said that, they are most trustworthy sources that we use
August 13th, 2020 at 2:54 am
triamterene generic brand name
August 13th, 2020 at 3:32 am
Sites of interest we have a link to
August 13th, 2020 at 4:25 am
always a large fan of linking to bloggers that I really like but don�t get a whole lot of link like from
August 13th, 2020 at 6:23 am
elimite canada
August 13th, 2020 at 6:33 am
Wow! This could be one particular of the most helpful blogs We ave ever arrive across on this subject. Actually Wonderful. I am also an expert in this topic therefore I can understand your effort.
August 13th, 2020 at 7:00 am
this blog loading? I am trying to determine if its a problem on my
August 13th, 2020 at 8:13 am
accutane costs canada
August 13th, 2020 at 9:10 am
always a huge fan of linking to bloggers that I appreciate but don�t get a good deal of link love from
August 13th, 2020 at 10:31 am
that may be the finish of this report. Right here you will obtain some sites that we think you will enjoy, just click the links over
August 13th, 2020 at 10:34 am
motilium over the counter australia
August 13th, 2020 at 10:58 am
This really answered the downside, thank you!
August 13th, 2020 at 11:03 am
The information talked about in the post are a number of the ideal offered
August 13th, 2020 at 12:01 pm
here are some links to websites that we link to because we believe they may be worth visiting
August 13th, 2020 at 1:09 pm
It as not that I want to duplicate your website, but I really like the design. Could you tell me which design are you using? Or was it especially designed?
August 13th, 2020 at 1:46 pm
Some truly prime articles on this web site , bookmarked.
August 13th, 2020 at 2:25 pm
tretinoin price uk
August 13th, 2020 at 2:45 pm
bactrim 800 mg
August 13th, 2020 at 2:50 pm
always a huge fan of linking to bloggers that I appreciate but don�t get a great deal of link like from
August 13th, 2020 at 3:28 pm
bactrim 800 mg coupon
August 13th, 2020 at 3:31 pm
Here are some of the internet sites we suggest for our visitors
August 13th, 2020 at 5:39 pm
one of our guests not too long ago suggested the following website
August 13th, 2020 at 6:13 pm
It as really a nice and helpful piece of information. I am glad that you shared this useful information with us. Please keep us up to date like this. Thanks for sharing.
August 13th, 2020 at 7:48 pm
This really solved my problem, thank you!
August 13th, 2020 at 8:09 pm
Here are several of the web sites we suggest for our visitors
August 13th, 2020 at 8:47 pm
levitra canadian online pharmacy
August 13th, 2020 at 8:52 pm
we like to honor lots of other world-wide-web web pages around the web, even when they aren�t linked to us, by linking to them. Beneath are some webpages worth checking out
August 13th, 2020 at 9:28 pm
lexapro wellbutrin
August 13th, 2020 at 10:40 pm
Right now it appears like BlogEngine is the top blogging platform out there right now. (from what I ave read) Is that what you are using on your blog?
August 13th, 2020 at 10:40 pm
usually posts some quite exciting stuff like this. If you are new to this site
August 14th, 2020 at 12:15 am
sure, analysis is paying off. Seriously handy perspective, many thanks for sharing.. Truly handy point of view, many thanks for expression.. Fantastic beliefs you have here..
August 14th, 2020 at 12:59 am
below you�ll find the link to some sites that we think you need to visit
August 14th, 2020 at 1:18 am
although websites we backlink to below are considerably not connected to ours, we really feel they may be actually worth a go via, so possess a look
August 14th, 2020 at 3:16 am
IE still is the marketplace chief and a large portion of other people will leave out
August 14th, 2020 at 4:02 am
hydrochlorothiazide 25 mg without prescription
August 14th, 2020 at 4:45 am
Thanks-a-mundo for the article.Much thanks again. Really Cool.
August 14th, 2020 at 4:54 am
What’s up i am kavin, its my first occasion to commenting anyplace, when i read this article i thought i could also make comment due
to this good piece of writing.
August 14th, 2020 at 4:56 am
The info talked about inside the post are several of the best obtainable
August 14th, 2020 at 5:09 am
After exploring a few of the articles on your blog, I seriously appreciate
your technique of blogging. I saved it to my bookmark webpage list and will be checking back in the near future.
Take a look at my web site as well and let me know your opinion.
August 14th, 2020 at 6:20 am
we came across a cool website that you just may well appreciate. Take a appear if you want
August 14th, 2020 at 6:25 am
discount valtrex online
August 14th, 2020 at 7:02 am
This is one awesome blog article. Great.
August 14th, 2020 at 7:35 am
singulair rx coupon
August 14th, 2020 at 8:57 am
check beneath, are some absolutely unrelated sites to ours, even so, they may be most trustworthy sources that we use
August 14th, 2020 at 9:06 am
Outstanding post, I believe people should larn a lot from this weblog its very user friendly.
August 14th, 2020 at 10:09 am
It’s hard to say
August 14th, 2020 at 10:32 am
The information talked about inside the report are a number of the best obtainable
August 14th, 2020 at 11:15 am
Sites of interest we have a link to
August 14th, 2020 at 11:39 am
finpecia without prescription
August 14th, 2020 at 1:28 pm
magnificent points altogether, you simply gained a brand new reader. What would you recommend in regards to your post that you made some days ago? Any positive?
August 14th, 2020 at 2:20 pm
very few web sites that take place to become comprehensive below, from our point of view are undoubtedly well really worth checking out
August 14th, 2020 at 3:21 pm
usually posts some quite fascinating stuff like this. If you�re new to this site
August 14th, 2020 at 4:45 pm
Some genuinely superb content on this website , thankyou for contribution.
August 14th, 2020 at 5:53 pm
I truly appreciate this blog article.Much thanks again.
August 14th, 2020 at 6:37 pm
prozac drug
August 14th, 2020 at 8:24 pm
tetracycline online without prescription
August 14th, 2020 at 9:16 pm
Perfectly pent written content, Really enjoyed examining.
August 14th, 2020 at 9:30 pm
prednisone 50 mg tablet price
August 14th, 2020 at 9:52 pm
trazodone 50 mg price canada
August 14th, 2020 at 10:15 pm
There is certainly a lot to find out about this issue. I like all of the points you have made.
August 15th, 2020 at 1:01 am
I was suggested this blog by my cousin. I am not sure whether this post is written by him as no one else know such detailed about my problem. You are amazing! Thanks!
August 15th, 2020 at 2:42 am
Thanks for sharing this good post. Very interesting ideas! (as always, btw)
August 15th, 2020 at 5:07 am
lopressor 25 mg
August 15th, 2020 at 5:30 am
Souls in the Waves Great Morning, I just stopped in to go to your web site and thought I ad say I liked myself.
August 15th, 2020 at 8:58 am
finasteride 0.1
August 15th, 2020 at 9:41 am
very few web sites that happen to be in depth beneath, from our point of view are undoubtedly nicely worth checking out
August 15th, 2020 at 10:19 am
lasix 50 mg
August 15th, 2020 at 10:58 am
malegra 50 for sale
August 15th, 2020 at 11:31 am
price atenolol
August 15th, 2020 at 11:32 am
You actually make it appear so easy together with your presentation however I in finding this
August 15th, 2020 at 12:45 pm
fluoxetine brand name uk
August 15th, 2020 at 1:02 pm
order dapoxetine
August 15th, 2020 at 1:13 pm
Hi, the whole thing is going nicely here and ofcourse every one is sharing information, that’s truly fine, keep upwriting.
August 15th, 2020 at 3:47 pm
This awesome blog is really interesting as well as informative. I have picked up many interesting stuff out of this amazing blog. I ad love to return again soon. Thanks!
August 15th, 2020 at 4:12 pm
triamterene 1300 mg
August 15th, 2020 at 7:08 pm
buy vermox nz
August 15th, 2020 at 8:04 pm
flagyl generic price
August 15th, 2020 at 8:07 pm
I will not talk about your competence, the article simply disgusting
August 15th, 2020 at 10:56 pm
toradol coupon
August 15th, 2020 at 10:59 pm
Keep up the fantastic piece of work, I read few articles on this site and I think that your site is real interesting and contains bands of superb info.
August 15th, 2020 at 11:41 pm
xenical tablets 120mg
August 15th, 2020 at 11:44 pm
motilium canada otc
August 16th, 2020 at 12:28 am
where can i buy clomid 100mg
August 16th, 2020 at 1:33 am
Yeezy 380…
http://www.airmax97.us.com/ Air Max 97…
August 16th, 2020 at 1:49 am
Pretty! This has been an incredibly wonderful article. Many thanks for supplying these details.
August 16th, 2020 at 3:07 am
malegra fxt
August 16th, 2020 at 6:04 am
This unique blog is really interesting as well as diverting. I have picked up a lot of handy tips out of this amazing blog. I ad love to return every once in a while. Thanks a lot!
August 16th, 2020 at 7:17 am
Yeezy Supply…
http://www.yeezy380.us.com/ Yeezy 380…
August 16th, 2020 at 8:54 am
usually posts some quite exciting stuff like this. If you are new to this site
August 16th, 2020 at 8:55 am
Im grateful for the blog post.Really looking forward to read more. Will read on
August 16th, 2020 at 11:05 am
allopurinol no rx
August 16th, 2020 at 11:47 am
Wonderful article! We are linking to this particularly great article on our website. Keep up the great writing.
August 16th, 2020 at 3:26 pm
how much is 5mg cialis
August 16th, 2020 at 6:53 pm
Nike Shoes…
http://www.yeezy-shoes.in.net/ Yeezy Shoes…
August 16th, 2020 at 7:43 pm
where to buy valtrex
August 16th, 2020 at 10:43 pm
where to buy antabuse in canada
August 16th, 2020 at 11:06 pm
Here is a great Weblog You might Obtain Fascinating that we encourage you to visit.
August 17th, 2020 at 1:17 am
medrol 4
August 17th, 2020 at 4:09 am
amoxil 250g
August 17th, 2020 at 4:30 am
cipro otc in mexico
August 17th, 2020 at 4:37 am
prednisone 200 mg tablets
August 17th, 2020 at 7:06 am
best price for lipitor
August 17th, 2020 at 8:02 am
tetracycline 300
August 17th, 2020 at 8:53 am
You made some nice points there. I did a search on the subject and found most guys will approve with your site.
August 17th, 2020 at 9:05 am
below you will discover the link to some web pages that we think it is best to visit
August 17th, 2020 at 9:37 am
that will be the finish of this post. Right here you will locate some websites that we assume you�ll value, just click the hyperlinks over
August 17th, 2020 at 11:42 am
Perfectly composed content , thanks for entropy.
August 17th, 2020 at 2:34 pm
Thank you, I have recently been looking for info about this subject for ages and yours is the best I ave discovered till now. But, what about the bottom line? Are you sure about the source?
August 17th, 2020 at 5:57 pm
prazosin 2
August 17th, 2020 at 6:12 pm
There is definately a great deal to find out about this subject. I really like all of the points you ave made.
August 17th, 2020 at 6:35 pm
drug robaxin 500mg
August 17th, 2020 at 10:21 pm
Wow, incredible blog layout! How long have you been blogging for? you made blogging look easy. The overall look of your site is great, let alone the content!. Thanks For Your article about sex.
August 17th, 2020 at 10:22 pm
You certainly put a fresh spin on a subject that as been discussed for
August 17th, 2020 at 11:10 pm
colchicine 1 mg tab
August 17th, 2020 at 11:34 pm
priligy for sale uk
August 18th, 2020 at 12:23 am
There as certainly a great deal to find out about this issue. I really like all the points you ave made.
August 18th, 2020 at 1:20 am
gabapentin 1500
August 18th, 2020 at 1:34 am
vermox tab 100 mg
August 18th, 2020 at 1:44 am
how to get prednisolone tablets
August 18th, 2020 at 3:13 am
We all speak a little about what you should speak about when is shows correspondence to simply because Maybe this has much more than one meaning.
August 18th, 2020 at 9:49 am
Wow, great blog article.Much thanks again. Awesome.
August 18th, 2020 at 10:53 am
how to order cytotec online
August 18th, 2020 at 11:53 am
Yeezy Boost 350 V2…
http://www.yeezy-shoe.us.com/ Yeezy Shoes…
August 18th, 2020 at 12:05 pm
5 mg arimidex
August 18th, 2020 at 1:07 pm
You made some good points there. I looked on the web to learn more about the issue and found most people will go along with your views on this web site.
August 18th, 2020 at 4:02 pm
Really informative blog article.Really looking forward to read more. Really Cool.
August 18th, 2020 at 4:16 pm
Yeezy Mafia…
http://www.adidasyeezy.us.com/ Adidas Yeezy…
August 18th, 2020 at 4:28 pm
order albenza online
August 18th, 2020 at 11:49 pm
acyclovir cost in india
August 19th, 2020 at 12:08 am
best price malegra fxt canada
August 19th, 2020 at 4:21 am
hydroxychloroquine name brand
August 19th, 2020 at 5:39 am
sildenafil without prescription from canada
August 19th, 2020 at 7:20 am
propecia 0.5 daily
August 19th, 2020 at 7:26 am
cost of phenergan gel
August 19th, 2020 at 9:23 am
That will be the finish of this write-up. Right here you�ll come across some web pages that we believe you�ll value, just click the hyperlinks.
August 19th, 2020 at 10:01 am
Sites of interest we’ve a link to
August 19th, 2020 at 1:17 pm
dipyridamole generic
August 19th, 2020 at 2:04 pm
sumycin drug
August 19th, 2020 at 2:35 pm
finpecia tablet
August 19th, 2020 at 2:52 pm
buspar 30
August 19th, 2020 at 5:33 pm
You have noted very interesting details ! ps decent web site. He that will not sail till all dangers are over must never put to sea. by Thomas Fuller.
August 19th, 2020 at 7:43 pm
world is changing
August 19th, 2020 at 10:15 pm
gabapentin 1000
August 19th, 2020 at 10:37 pm
One of our guests a short while ago encouraged the following website.
August 19th, 2020 at 10:58 pm
avana 200mg
August 19th, 2020 at 11:15 pm
Kobe Bryant Jersey 24…
http://www.yeezyadidas.fr/ Adidas Yeezy…
August 20th, 2020 at 12:01 am
avana canada
August 20th, 2020 at 12:23 am
finpecia without prescription
August 20th, 2020 at 12:42 am
Below you�ll find the link to some web-sites that we consider you need to visit.
August 20th, 2020 at 3:20 am
ampicillin on line cheap quick shipment
August 20th, 2020 at 4:28 am
neurontin 200 mg capsules
August 20th, 2020 at 7:48 am
Hello Dear, are you truly visiting this site daily,
if so afterward you will without doubt take fastidious knowledge.
August 20th, 2020 at 8:45 am
although internet sites we backlink to beneath are considerably not connected to ours, we feel they’re basically really worth a go by means of, so possess a look
August 20th, 2020 at 8:54 am
diclofenac 500g
August 20th, 2020 at 1:33 pm
generic flagyl 500 mg
August 20th, 2020 at 2:14 pm
Wow! This can be one particular of the most beneficial blogs We ave ever arrive across on this subject. Actually Wonderful. I am also an expert in this topic therefore I can understand your hard work.
August 20th, 2020 at 4:36 pm
You are my aspiration, I have few blogs and very sporadically run out from post. Fiat justitia et pereat mundus.Let justice be done, though the world perish. by Ferdinand I.
August 20th, 2020 at 5:41 pm
advair 2019 coupon
August 20th, 2020 at 7:25 pm
There is apparently a lot to identify about this. I think you made certain good points in features also.
August 21st, 2020 at 4:52 am
Jordan AJ 1…
http://www.supplyyeezy.us.com/ Yeezy Supply…
August 21st, 2020 at 6:51 am
hydrochlorothiazide 80 12.5 mg
August 21st, 2020 at 10:10 am
albendazole cost australia
August 21st, 2020 at 10:20 am
how to buy cialis online uk
August 21st, 2020 at 10:55 am
colchicine prices canada
August 21st, 2020 at 2:05 pm
tetracycline 500mg capsule price
August 21st, 2020 at 4:29 pm
What as up, I read your new stuff daily. Your humoristic style is witty, keep up the good work!
August 21st, 2020 at 5:27 pm
clomid for sale india
August 21st, 2020 at 10:48 pm
Jordan 1s…
http://www.nikefactory.us.com/ Nike Outlet…
August 21st, 2020 at 11:24 pm
brand name wellbutrin cost
August 22nd, 2020 at 1:02 am
medrol tablet price
August 22nd, 2020 at 5:12 am
cost of strattera generic
August 22nd, 2020 at 7:02 am
where to order plaquenil
August 22nd, 2020 at 10:44 am
always a significant fan of linking to bloggers that I enjoy but really don’t get a great deal of link adore from
August 22nd, 2020 at 11:28 am
5mg finasteride
August 22nd, 2020 at 1:12 pm
fluoxetine 40 mg online
August 22nd, 2020 at 2:03 pm
phenergan 25mg tablets price
August 22nd, 2020 at 2:23 pm
prednisone 10 mg price in india
August 22nd, 2020 at 10:45 pm
lipitor uk price
August 23rd, 2020 at 3:19 am
I do consider all of the concepts you have presented to your
post. They are really convincing and will certainly work. Nonetheless,
the posts are too brief for starters. Could you please extend them a
little from subsequent time? Thank you for the
post.
August 23rd, 2020 at 3:46 am
augmentin 625mg price in usa
August 23rd, 2020 at 6:23 am
prozac 60 mg price
August 23rd, 2020 at 7:42 am
seroquel medicine
August 23rd, 2020 at 8:15 am
plaquenil for lupus
August 23rd, 2020 at 9:09 am
triamterene generic
August 23rd, 2020 at 9:35 am
generic vermox cheap
August 23rd, 2020 at 10:23 am
buy silagra online
August 23rd, 2020 at 1:19 pm
Air Jordan 1…
http://www.yeezymafia.us.com/ Yeezy…
August 23rd, 2020 at 7:06 pm
indocin in india
August 24th, 2020 at 12:55 am
ivermectin 4 tablets price
August 24th, 2020 at 1:54 am
generic flagyl cost
August 24th, 2020 at 1:57 am
prednisolone acetate
August 24th, 2020 at 3:33 am
erythromycin 333 mg capsules
August 24th, 2020 at 5:56 am
I think this is one of the most vital info for me. And i am glad reading your article.
But should remark on few general things, The site style
is ideal, the articles is really great : D. Good job, cheers
August 24th, 2020 at 8:41 am
Hi my loved one! I wish to say that this post is awesome,
nice written and come with approximately all vital infos.
I’d like to look extra posts like this .
August 24th, 2020 at 9:44 am
glucophage costs
August 24th, 2020 at 1:55 pm
where can you get bactrim
August 24th, 2020 at 2:17 pm
vardenafil buy
August 24th, 2020 at 3:03 pm
neurontin pfizer
August 24th, 2020 at 3:25 pm
seroquel 300 mg generic
August 24th, 2020 at 4:59 pm
Does your blog have a contact page? I’m having a
tough time locating it but, I’d like to shoot
you an e-mail. I’ve got some suggestions for your blog you might be interested in hearing.
Either way, great blog and I look forward to seeing it improve
over time. cheap flights 31muvXS
August 24th, 2020 at 6:49 pm
Your website offered us with valuable info to work on.
August 24th, 2020 at 9:16 pm
robaxin 800 mg
August 24th, 2020 at 9:37 pm
avana 50 mg
August 24th, 2020 at 10:15 pm
always a huge fan of linking to bloggers that I really like but really don’t get a lot of link appreciate from
August 24th, 2020 at 10:47 pm
how to order cipro
August 24th, 2020 at 11:48 pm
price of zoloft 50 mg
August 25th, 2020 at 5:16 am
Dior Jordan 1…
http://www.airjordan-1.us/ Air Jordan 1…
August 25th, 2020 at 6:17 am
whoah this weblog is wonderful i really like reading your articles.
Stay up the good work! You recognize, many people are looking around for
this info, you can help them greatly. 3gqLYTc
cheap flights
August 25th, 2020 at 6:35 am
cost of 20mg cialis tablets
August 25th, 2020 at 8:01 am
although sites we backlink to beneath are considerably not associated to ours, we feel they’re really really worth a go by way of, so possess a look
August 25th, 2020 at 8:38 am
tadalafil price in canada
August 25th, 2020 at 11:37 am
levitra purchase canada
August 25th, 2020 at 11:52 am
The next time I learn a blog, I hope that it doesnt disappoint me as much as this one. I mean, I do know it was my option to learn, however I actually thought youd have one thing interesting to say. All I hear is a bunch of whining about one thing that you can repair should you werent too busy on the lookout for attention.
August 25th, 2020 at 12:34 pm
That is a very good tip especially to those fresh to the blogosphere. Brief but very precise information Thank you for sharing this one. A must read post!
August 25th, 2020 at 3:27 pm
plavix 75 mg tablet price in india
August 25th, 2020 at 4:06 pm
diclofenac gel canada
August 25th, 2020 at 6:48 pm
discount cymbalta
August 25th, 2020 at 7:17 pm
wellbutrin 50 mg
August 25th, 2020 at 7:28 pm
Really informative article.Really looking forward to read more.
August 25th, 2020 at 9:06 pm
I love reading through a post that will make people
think. Also, thanks for allowing for me to comment!
cheap flights yynxznuh
August 26th, 2020 at 2:15 am
acyclovir capsules 800mg
August 26th, 2020 at 3:30 am
Good information. Lucky me I ran across your site by chance (stumbleupon).
I’ve saved it for later! cheap flights 32hvAj4
August 26th, 2020 at 4:10 am
What’s up, everything is going nicely here and ofcourse
every one is sharing information, that’s actually excellent, keep
up writing.
August 26th, 2020 at 8:07 am
Sites of interest we have a link to
August 26th, 2020 at 8:16 am
generic viagra soft tabs
August 26th, 2020 at 8:30 am
Here is a good Blog You might Find Exciting that we Encourage You
August 26th, 2020 at 10:37 am
please stop by the web sites we follow, such as this a single, as it represents our picks through the web
August 26th, 2020 at 11:06 am
buy cheap avodart no rx
August 26th, 2020 at 11:28 am
indocin 500
August 26th, 2020 at 11:48 am
Have you ever thought about adding a little bit more than just your articles?
I mean, what you say is important and all.
However just imagine if you added some great pictures or video clips to give your
posts more, “pop”! Your content is excellent but
with images and videos, this site could undeniably be one of the
most beneficial in its niche. Wonderful blog!
August 26th, 2020 at 11:54 am
below you will locate the link to some web-sites that we feel you ought to visit
August 26th, 2020 at 12:03 pm
advair diskus no prescription
August 26th, 2020 at 12:46 pm
buy arimidex 1mg
August 26th, 2020 at 1:23 pm
we like to honor numerous other online web-sites on the net, even when they aren�t linked to us, by linking to them. Underneath are some webpages really worth checking out
August 26th, 2020 at 2:01 pm
cheapest amoxicillin 875
August 26th, 2020 at 2:32 pm
cheap proscar online
August 26th, 2020 at 5:52 pm
buspar online
August 26th, 2020 at 6:36 pm
yE4nv5 hi guys http://xnxx.in.net/
August 26th, 2020 at 7:27 pm
hydroxychloroquine sulfate 200mg
August 26th, 2020 at 7:46 pm
You really make it seem so easy with your presentation but
August 26th, 2020 at 11:21 pm
here are some links to web pages that we link to mainly because we think they may be worth visiting
August 26th, 2020 at 11:46 pm
avodart cost australia
August 27th, 2020 at 4:36 am
Hey! I know this is kind of off topic but I was wondering which blog platform are you using for this website?
I’m getting fed up of Wordpress because I’ve had problems with hackers and I’m looking at alternatives for another
platform. I would be great if you could point me in the direction of a good platform.
August 27th, 2020 at 9:10 am
how much is seroquel 300 mg
August 27th, 2020 at 9:13 am
Awesome things here. I am very happy to peer
your post. Thank you a lot and I’m looking ahead to contact you.
Will you please drop me a e-mail?
August 27th, 2020 at 11:54 am
Kobe Bryant Jersey…
http://www.airmaxclearancesale.us/ Air Max Clearance Sale…
August 27th, 2020 at 12:46 pm
pharmacy best price advair canada
August 27th, 2020 at 1:28 pm
I’ve been surfing online more than 4 hours today, yet I never
found any interesting article like yours. It is pretty worth enough
for me. Personally, if all site owners and bloggers made good content as you
did, the net will be much more useful than ever before.
August 27th, 2020 at 1:44 pm
accutane from mexico
August 27th, 2020 at 2:13 pm
malegra for sale
August 27th, 2020 at 2:26 pm
real beauty page normal adult dose lexapro Scientists in the Netherlands and the US carried out a major review of 37 trials involving almost 2,800 people
August 27th, 2020 at 2:32 pm
I’d like to open an account chloroquine and fluoroquinolone resistance dissertation In addition, he spent more millions on a private jet to transport the Marlins throughout the season, along with a personal nutrition chef, and hired 10 additional scouts.
August 27th, 2020 at 2:39 pm
Do you know what extension he’s on? nix permethrin lice treatment reviews The study measured changes in two different measures of kidney function, eGFR and mGFR
August 27th, 2020 at 2:45 pm
What sort of music do you listen to? mestinon thyroid He was also found guilty of having thousands of images of child porn on the computer he brought into the nursery to help the children with their IT skills and a further four on the laptop at his then home in Stirling.
August 27th, 2020 at 2:51 pm
One moment, please methocarbamol 500mg for dogs side effects There is also always top flight musical entertainment, including Winston (Merritone) Blake.
August 27th, 2020 at 2:57 pm
Yes, I love it! rumalaya forte tabletki cena Body language plays a big part in getting the message over, such as the palm of the hand facing downwards to indicate ‘calm down’.
August 27th, 2020 at 3:17 pm
I’d like to speak to someone about a mortgage manhood max uk
Tim Lake (Domhnall Gleeson) grows up with his mysteriously well-off, bohemian family in Cornwall, having suppers on the beach and playing table tennis. Then, on his 21st birthday, Tim’s dad (Bill Nighy, almost exploding with tics denoting wry, diffident charm) tells him that the men of the family have the ability to travel back in time. If they go somewhere dark – a wardrobe, say – clench their fists and focus, they can nip into a segment of life that they have already lived, and tweak things for the better.
August 27th, 2020 at 3:18 pm
Not available at the moment bactrim ds vs bactrim Researchers from the University of Oregon recruited 60 university students, including 27 smokers. Half of the group learned a meditation technique called integrative body-mind training, or IBMT. Subjects practiced for five hours over a two-week period. The remaining subjects followed the same schedule but practiced relaxation therapy, where they concentrated on releasing tension from different parts of the body.
August 27th, 2020 at 3:18 pm
I’m afraid that number’s ex-directory buying cialis craigslist Hotton, 47, admitted on Monday to having scammed cash from the long-delayed Broadway musical’s producers by “finding” millionaire investors who turned out to be fictional characters. When producers got suspicious about one of Hotton’s phantom investors, he had him suddenly die from malaria, court papers say.
August 27th, 2020 at 3:18 pm
I love this site arcoxia etoricoxib msd 90 mg para que sirve “We’re paid to get out there and play, not watch,” Peterman said. “You definitely want to be out there, I don’t know what it will do to my chances (of starting), but you definitely want to be out there playing.”
August 27th, 2020 at 3:18 pm
Very interesting tale vegetal vigra australia
Purdy said the case was too serious to be dealt with in the magistrates court, given his past convictions. He accepted that Belmar was living in the community on prescription medication, but added: “Something has clearly gone wrong.
August 27th, 2020 at 3:18 pm
An estate agents doxycycline hyc 100mg It’s possible other companies have suffered similar problems since flooding began last week but have not yet been able to assess their damage. An aerial survey of the flood area on Thursday revealed up to two dozen overturned oil storage tanks, state regulators said. Releases from those tanks could not be immediately confirmed.
August 27th, 2020 at 3:19 pm
What company are you calling from? topamax no prescription needed
The White House on Thursday beat back an attempt byRepublicans to link a measure to approve Keystone to a bill toraise the debt limit, saying it would reject legislation thatincludes that provision.
August 27th, 2020 at 3:19 pm
I’m interested in this position perrigo clindamycin phosphate foam 1 Thereâs this notion that there was no sportstalk radio before Bill Mazer hit New York City in 1964 to stake his claim as the Christopher Columbus of yakk when he started taking calls on WNBC-AM. Thatâs sort of a myth, but whoâs counting? A cat named Benny the Fan had done a show. Marty Glickman, too.
August 27th, 2020 at 3:21 pm
d http://dfdgtgyhyhuujuju.com
August 27th, 2020 at 3:21 pm
How long are you planning to stay here? does kamagra always work The Israelis and Arabs could be a powerful economic force and the Arab radical leadership is very afraid of this since they would not be involved (or get their baksheesh).
August 27th, 2020 at 3:22 pm
Not available at the moment metformin online australia The World Gold Council estimates there are about 2,000 tonnes of gold locked away in temples - worth about $84 billion at current prices - which Indian devotees have offered in the form of jewelry, bars, coins and even replicas of body parts, in the hope of winning favors from the gods or in thanks for blessings received and health restored.
August 27th, 2020 at 3:23 pm
What’s the last date I can post this to to arrive in time for Christmas? fluoxetine buy uk The partisan pivot may reflect the evolution of media coverage away from the role of President Barack Obama and toward Congress, where members are actively debating the policies. In late July a bipartisan group led by liberal Democrats and libertarian Republicans in the House nearly defunded the NSA’s dragnet phone-record collection.
August 27th, 2020 at 3:23 pm
I’m a member of a gym caverta generic viagra caverta caverta pillshoprxcom The news comes as Obama and fellow Democrats are trying tostave off Republican attempts to delay the healthcare reform’slaunch with the threat of shutting down the federal governmentor risking a U.S. default on its credit.
August 27th, 2020 at 3:23 pm
I’m interested in this position can you get high off benadryl-d China challenged the tire tariff at the WTO, and lost.Within a week of the United States saying it wanted to litigatethe broiler dispute, China slapped anti-dumping duties on morethan $3 billion worth of U.S. cars. Those duties are now thesubject of a separate WTO complaint by the United States.
August 27th, 2020 at 3:24 pm
Can you hear me OK? pepcid prescription strength side effects With the verdict drawing near, police and city leaders in Sanford and other parts of Florida said they have taken precautions for the possibility of mass protests or even civil unrest if Zimmerman, whose father is white and whose mother is Hispanic, is acquitted.
August 27th, 2020 at 3:24 pm
I stay at home and look after the children ms wellbutrin xl 150 In between “delay” and “do-over,” is “dismantle,” taking the new law apart piece by piece in order to accelerate its collapse under its own weight. The Obamacare advocates who say the public will never go for repeal if it means losing the goodies that are being bestowed upon them are probably right. This means the opponents of the new law have to act in such a way as to force hard choices above and beyond the hard choices that reality is already hitting them with. The premium increases, layoffs, and conversion of full time jobs into part time jobs are not coincidental; they are a direct result of the costs Obamacare is already imposing on private insurance and on employers.
August 27th, 2020 at 3:25 pm
Where are you calling from? where can i buy viagra in cyprus “Obviously, the Petit family suffered more than I can imagine, and I would never compare their loss with mine. But when someone does something like what [my father] did, his family suffers, too.
August 27th, 2020 at 3:25 pm
Through friends lek za mrsavljenje xenical
Apodaca, who had served in Afghanistan, calmly testified earlier this year about the day in 2009 when he emptied eight rounds into Gonzalez-Galeana, then jumped into a get-away car driven by an accomplice.
August 27th, 2020 at 3:25 pm
Why did you come to ? avapro 500 mg Even still, the risk from eating package salads is tiny, said Scott Horsfall, chief executive officer of the California Leafy Greens Marketing Agreement, a trade group of shippers of green leaf products.
August 27th, 2020 at 3:26 pm
Would you like to leave a message? lipitor 20mg uk “Cowards,” says his grandmother, Barbara Jones, sitting in the den of her Jackson home. “If somebody has the nerve to murder another human being, shouldn’t they also have the nerve to look them in the eyes when they do it?”
August 27th, 2020 at 3:28 pm
I’m sorry, I didn’t catch your name himcolin oint Mora says she was diagnosed with an aneurysm in a cerebral artery on April 14, 2011 and sent home from the hospital with the warning she could be dead within a month, although the surgeon who made the diagnosis denies he gave such a warning.
August 27th, 2020 at 3:28 pm
Could you ask her to call me? generic plaquenil country singer with his own British television series, according to his biography on the website of the Grand Ole Opry.
August 27th, 2020 at 3:28 pm
How much were you paid in your last job? alesse birth control side effects symptoms California Governor Jerry Brown announced plans on Friday to seek an injunction to bar Bay Area Rapid Transit Districtworkers from striking for 60 days if the transit agency and itsemployees fail to resolve their contract dispute by Sunday.
August 27th, 2020 at 3:29 pm
I work for myself vegetal vigra uk
Moss, 39, also opened up about the backlash she received for ushering in the waifish trend after posing for Calvin Klein in 1993 - which many believe led to the glorification of attaining a size zero waist.
August 27th, 2020 at 3:29 pm
Could I have , please? lipitor consumer reviews Smith hit Stephen Hill, then Jeremy Kerley, then Hill again for three quick completions. He checked out of several plays on the drive, calling audibles that worked, particularly on the final play, a six-yard run by Bilal Powell that put the Jets at the Falcons 25, making it a relatively easy kick for Folk.
August 27th, 2020 at 3:30 pm
Do you need a work permit? mediclinic middle east ceo “We’re feeling hopeful and optimistic,” said Madeleine’s dad Gerry on the BBC’s “Crimewatch” program. “When it’s a special occasion, when you should be your happiest and Madeleine’s not there, that’s when it really hits home,” he said.
August 27th, 2020 at 3:30 pm
We’ll need to take up references cmartin.onlinehealth.news The AHDA has already been in production vehicles for a number of years, and it relies on radar and stereoscopic cameras to detect the speed of the traffic ahead. However, in contrast to the standard radar cruise control – which utilizes millimeter-wave radar to detect other vehicles), Cooperative-adaptive Cruise Control uses 700-MHz band vehicle-to-vehicle ITS communications; and this allows for the car to transmit acceleration and deceleration data from preceding vehicles. This in turn allows subsequent vehicles to adjust the speeds accordingly.
August 27th, 2020 at 3:31 pm
Withdraw cash fluticasone nasal spray otc uk Former Penney Chief Executive Officer Ron Johnson viewedMartha Stewart as key to his vision for remaking the strugglingretailer. Johnson, who failed to win over shoppers andinvestors, was ousted in April.
August 27th, 2020 at 3:31 pm
I’m sorry, I didn’t catch your name lixus clomid reviews When considering the average indebted household owes a balance of $6,591, according to CardHub’s 2013 credit card study, a middle-of-the-road balance transfer card could be worth as much as $1,000 in avoided fees and finance charges.
August 27th, 2020 at 3:31 pm
I don’t know what I want to do after university black ant pills canada
âI think the way I need to treat it is itâs an opportunity,â he said right after the round. âThatâs the way I have been looking at every round this week. I know Iâm going to go to the media room and I know someone is going to mention that Iâm 43 and that Iâm old and how many more chances am I going to have?
August 27th, 2020 at 3:32 pm
A jiffy bag discount cipro Most of the OPEC member’s exports head to Asia, where theUnited States has worked with Iran’s top four customers China,India, Japan and South Korea to push them towards alternativesuppliers. The four have cut purchases from Iran by more than afifth in the first half of this year, over and above thereductions made last year.
August 27th, 2020 at 3:34 pm
Insert your card best deal on cialis “It is my team now,” Moyes said. “I have taken over, I’m in charge. I will use the ex-manager as much as I can because of his knowledge, but it is my team now and I have to take responsibility for that.
August 27th, 2020 at 3:34 pm
I’ve been made redundant flagyl 500 mg tab The shopping mall massacre perpetrated in Kenya by Islamist fanatics has shone a spotlight on their grotesquely brutal method of financing terror: They slaughter elephants to sell tusk ivory to a ravenous underground market.
August 27th, 2020 at 3:34 pm
Another year albuterol 5mg ml “It is too late to avoid a hard-landing,” said Patrick Chovanec from Silvercrest Asset Management and a former professor at Beijing’s Tsinghua University. “To keep growth going they have to push extremely high levels of investment to even more extreme levels, and that is becoming very hard to do and very hard to finance.”
August 27th, 2020 at 3:35 pm
I’d like a phonecard, please rosuvastatin cost australia Four different trim levels will be available – Standard, Loft, Lodge and Suite. Standard equipment includes a satnav system that provides a “dynamic range display” and a view of public charging stations and their availability.
August 27th, 2020 at 3:35 pm
Where did you go to university? erexine The Florida High School Athletic Association and the South Gulf Football Officials Association said Sam was not penalized for praying
August 27th, 2020 at 3:36 pm
Not in at the moment pacheco orlistat Pakistan has strongly denied any involvement in the attack and has said it is committed to the ceasefire agreement. Pakistani military spokesmen were not immediately available for comment on the latest Indian statement.
August 27th, 2020 at 3:37 pm
I’d like to cancel this standing order how old do you have to be to buy vermox They called for a “standardized approach” to identify cases of infectious encephalitis among donors and for the establishment of a case definition with specific clinical criteria that could be used for screening.
August 27th, 2020 at 3:37 pm
How many more years do you have to go? neurontin price increase Democrats are hoping that Republicans, mindful of the party’s poor performance in recent national elections among Hispanics, will support a comprehensive bill that tackles many issues such as citizenship, expanded visas and border security. But the House Republicans have thus far been working on separate bills for each issue.
August 27th, 2020 at 3:37 pm
We’d like to offer you the job champion performance heavyweight gainer 900 “The nation’s credit is at risk because of theadministration’s refusal to sit down and have a conversation,”Boehner told ABC’s “This Week,” adding that there were notenough votes in the House of Representatives to pass a “clean”debt limit bill, without any conditions attached.
August 27th, 2020 at 3:37 pm
Sorry, I’m busy at the moment megalis 10 benefits 4. Don’t make your management team too big. You need to have people representing the key areas of the business, but keep it tight otherwise it will become impossible to conduct useful discussions and make decisions.
August 27th, 2020 at 3:38 pm
How do you do? paroxetine mg
Kennedy, who suffers from mental illness, was a Democratic House member from Rhode Island from 1995 to 2011. John F. Kennedy was his uncle, and his father, former senator Edward Kennedy of Massachusetts, was a longtime supporter of increased health care coverage for all Americans.
August 27th, 2020 at 3:39 pm
I work for myself olanzapine cost australia It expects to produce over 60 billion cubic metres (bcm) ofgas by 2016, compared with 42 bcm forecast for 2013, and 100 bcmin 2020, of which more than half will be produced at newlyacquired projects.
August 27th, 2020 at 3:40 pm
I quite like cooking cita previa online itv extremadura SMI’s international ratings are equalised with the Indonesia sovereign (BBB-/Stable), reflecting ownership by the central government through the Ministry of Finance (MOF) and the important strategic role the entity has in the development of Indonesia’s infrastructure. SMI’s national rating was upgraded as a result of the re-assessment of the link with the government under Fitch’s Rating of a Public Sector Entity methodology.
August 27th, 2020 at 3:40 pm
A financial advisor price of nexium otc
However, the lawsuit filed against Georgia by the cell phoneindustry association called CTIA, claims that by adding the $5fee, the state is setting cell phone rates, which it does nothave the legal power to do.
August 27th, 2020 at 3:41 pm
The National Gallery viagra rezeptfrei bestellen To cheering and applause from union autoworkers in Liberty, the Democrat tore into Congress, demanding that it fund the government and raise the debt ceiling without touching his signature accomplishment, the Affordable Care Act. “We’re not some banana republic,” he told more than 1,000 at the new Ford stamping plant near Claycomo. “This is not a deadbeat nation. We don’t run out on our tab.”
August 27th, 2020 at 3:42 pm
How do I get an outside line? cefixime dosage for uti Why? She lied to us about Benghazi, she covered up for a pedophile, and she accomplished nothing as Senator or Secretary of State. She missed her chance in 2008. I am sure the GOP would have a field day with her scandles and her racist remarks about white voters not voting for Obama. No more Bushs, and no more Clintons please. It will be 2016, not 1992.
August 27th, 2020 at 3:42 pm
I’d like to pay this in, please lamictal homeopath CUNY costs a fraction of what students pay at private institutions, and it beats most public universities, too.
August 27th, 2020 at 3:43 pm
Looking for a job metronidazole online pharmacy canada An American law firm is to conduct a top-to-bottom review of GlaxoSmithKlineâs Chinese operation after an admission from the drugs company that an ongoing corruption scandal is likely to hit its bottom line.
August 27th, 2020 at 3:43 pm
Photography price of fosamax 70 mg âYou know, the mistakes,â Fewell said. âHe had a critical play in the ballgame, on a fourth-down situation for us. He took an inside pass-rush move, and the quarterback escaped outside, and he lost contain and we lost the integrity of the defense. . . . Once he understands that, I think he will play within the framework.â
August 27th, 2020 at 3:43 pm
How long have you lived here? purchase cytotec (misoprostol) U.S. Bankruptcy Court Judge Steven Rhodes agreed to theexpedited hearing requested by Detroit’s emergency manager KevynOrr on Friday in the wake of a Michigan court judge’s order forOrr to withdraw Thursday’s Chapter 9 filing on stateconstitutional grounds.
August 27th, 2020 at 3:44 pm
I’ve been made redundant tetracycline mechanism of action A monthly rise in hiring in the 200,000 area, analysts say,should keep the Fed on track to start to pare its $85 billionpurchases of Treasuries and mortgage-backed securities as earlyas at its Sept. 17-18 meeting.
August 27th, 2020 at 3:44 pm
this post is fantastic amlodipine actavis 5 mg tabletten Polischuk said the role of condensate is gradually growing,especially for medium-size companies, as lower taxes aresupporting its extraction. Condensate may be added to oil toboost its quality. Condensate accounts for a large part ofRussia’s No. 2 gas firm Novatek’s business, he said.
August 27th, 2020 at 3:45 pm
Lost credit card priligy 30 mg rezeptfrei kaufen Farther south, the so-called Mile Marker 28 fire, which has blackened 27,000 acres close to the Oregon border, is 75 percent contained, with residents of 69 homes forced to flee allowed to return as of Wednesday.
August 27th, 2020 at 3:45 pm
I’d like to cancel this standing order manufacturer of dapoxetine in india The company also outlined a range of new products for thesecond half of the year, including a new Vanish stain removersoap bar for emerging markets and Durex Embrace, two so-called”pleasure gels” that provide a warming and tingling feeling.
August 27th, 2020 at 3:48 pm
Could I have a statement, please? differin buy online Having made his test debut for India in 1989 at age 16, Tendulkar has scored 15,837 runs in 198 tests and 18,426 runs in 463 one-day internationals. He is the only batsman to score a century â 100 runs in an innings â 100 times across both formats.
August 27th, 2020 at 3:49 pm
How much were you paid in your last job? buy flagyl antibiotic The issue is expected to value Alibaba at $60-$100 billion,and could raise $15 billion, making it one of the world’sbiggest internet IPOs and a much sought-after prize for bankersand stock exchanges.
August 27th, 2020 at 3:49 pm
Do you play any instruments? cost of prilosec at walgreens Dr. Donald Casey Jr., a general internist and chief medical officer for the NYUPN Clinically Integrated Network, wrote a commentary about the new study and offers ideas about how to fix things. It’s not a matter of doctors not doing their jobs properly, he said. Instead, “it’s that health care has gotten so complex.”
August 27th, 2020 at 3:49 pm
I’m interested in this position low cost cipro roma As I look back on 2010, my final full year as Reuters Editor-in-Chief, Iâm struck by how journalists and news organizations have been challenged with a steady stream of high-impact, global stories. The 3,000 men and women of Reuters answered those challenges.
August 27th, 2020 at 3:49 pm
What sort of music do you listen to? hyzaar vs cozaar Facing an Islamic insurgency that seeks to topple his government, establish a caliphate and impose Sharia law, he’s wielding dictatorial power to target the radicals and stifle dissent more broadly.
August 27th, 2020 at 3:50 pm
I’m doing a masters in law diflucan uk Speculation over who Bernanke’s successor could be hascaused anxiety in the market, with investors wondering howdifferent the next chair’s policies would be. The timing of theannouncement is also tricky as the Fed simultaneously considerswhen to begin pulling back its $85 billion a month in bondpurchases.
August 27th, 2020 at 3:50 pm
A company car buy buspar medication Brisbane-based Linc said its subsidiary, New Emerald Coal, had entered into a sales agreement for the project, but added that it would not make an upfront payment to acquire the mine. The deal includes the mining tenure, on-site assets and infrastructure.
August 27th, 2020 at 3:50 pm
this is be cool ivermectin stromectol Prince Andrew, 53, said that he was “grateful” for the apology, adding that the police have a difficult job to do and he is looking forward to “a safe walk in the garden in the future”.
ivermectin stromectol Prince Andrew, 53, said that he was “grateful” for the apology, adding that the police have a difficult job to do and he is looking forward to “a safe walk in the garden in the future”.
August 27th, 2020 at 3:51 pm
Can you hear me OK? espn radio viagra promotion 40 years of Democrat and Union rule. They looted Detroit and still will not give up trying to extract their ill gotten gains. The problem with socialism is that eventually you run out of other people’s money. Well, someday has finally arrived.
August 27th, 2020 at 3:51 pm
What qualifications have you got? maxocum australia
But Nic Norman-Smith, chief investment officer of Lentus Asset Management in Johannesburg, cautioned that Massmart may have to pay a premium to get into Kenya, given the limited number of available retailers that would fit its business model.
August 27th, 2020 at 3:53 pm
I’m interested in this position where to get nolvadex in canada Harry was greeted in Australia by throngs of fans as well as headlines that included, “Lock up your daughters Tony Abbott, Prince Harry is heading down under to party,” referring to the country’s prime minster and his two attractive, younger daughters.
August 27th, 2020 at 3:54 pm
How do you spell that? miglior prezzo kamagra
The Yankees Entertainment & Sports Network should benefit greatly, in terms of ratings, which have been subpar this season. YES has a chance to hit paydirt in the home finale. What looked to be a meaningless game should become another iconic moment in Yankees history. The prospect of seeing two of the storied franchiseâs most dependable, and revered, arms simultaneously bidding adieu to the Bronx should attract a major influx of eyeballs.
August 27th, 2020 at 3:55 pm
Could you tell me the dialing code for ? erythromycin 500 mg dosage Flows into European equities from U.S.-based fundsaccelerated in the week ended Sept. 18, according to Lipperdata, with the region’s stocks enjoying their third-biggestweekly net inflows since Lipper started to track the data in1992.
August 27th, 2020 at 3:55 pm
Is it convenient to talk at the moment? buy famciclovir online uk Eighteen other fishermen from the eastern provinces of Catanduanes and Camarines Norte also were unaccounted for. Authorities were hoping they took shelter in coves and nearby islands, said Office of Civil Defense regional director Bernardo Alejandro IV.
August 27th, 2020 at 3:56 pm
Could you tell me my balance, please? terbinafine hcl prices Speaking in Washington the president said:“As soon as Congress votes to reopen the government, it’s also got to vote to meet our country’s commitments — pay our bills; raise the debt ceiling. Because as reckless as a government shutdown is, the economic shutdown caused by America defaulting would be dramatically worse.”
August 27th, 2020 at 3:56 pm
I read a lot levofloxacin 500 mg tablets dosage He hasnât played a down of football since the 2011 preseason. Back then, he was an up-and-coming corner, a franchise building block for the Giants. Then he tore his right ACL in a preseason game against the Bears, instantly ending his season. A year later, after a furious rehab, he returned to training camp in Albany and promptly re-tore the ACL.
August 27th, 2020 at 3:56 pm
Your cash is being counted purchase zanaflex online Versar Inc, a projectmanagement company that has a hazardous waste segment jumped15.5 percent to $4.85.
August 27th, 2020 at 3:56 pm
What line of work are you in? how long for coumadin to get out of system The injuries are somewhat reminiscent of the days before shoulder belts in cars, although much more severe, said Dr. David Okonkwo of the University of Pittsburgh Medical Center, who isn’t involved with the survivors’ care.
August 27th, 2020 at 3:57 pm
I can’t hear you very well staxyn cost walmart Administration officials and independent economists have warned that failure to meet the deadline could trigger economic shock waves, sending the dollar downhill, causing interest rates to soar and freezing credit markets across the globe. It could thrust the U.S. into a recession worse than 2008, some officials say.
August 27th, 2020 at 3:57 pm
What do you do? dulcolax dosis maxima
One of its workers was the source of high-profile leaks of secret government surveillance information. The company fired that employee, Edward Snowden, on Tuesday after its stock dropped dramatically on Monday after news of the leak’s source broke. It is currently trading around $17 per share, 4 percent below Friday’s closing price.
August 27th, 2020 at 3:57 pm
I’ve got a part-time job tadalista europe The president jabbed Republican adversaries over immigrationand health care as well as housing. He argued that immigrationreform - which is languishing in the House - would help the U.S.housing market because undocumented people were important buyersof homes.
August 27th, 2020 at 3:59 pm
Have you got any qualifications? buy propranolol 10 mg The U.S. dollar edged slightly higher while the euro fell oncontinued expectations that the U.S. Federal Reserve will befirst among the major central banks to scroll back onultra-loose monetary policy. Yields on the 10-year U.S. Treasuryrose and Bunds rebounded.
August 27th, 2020 at 4:00 pm
A jiffy bag atenolol 50 mg tablet picture The new study was an attempt to separate the effects of testosterone and estrogen - most of which is made by the body from testosterone - on men’s sexual function, strength, muscle size and lean and fat mass, and to discover how much testosterone is needed for health.
August 27th, 2020 at 4:01 pm
Not in at the moment fda approved cialis online New Jersey Devils’ Michael Ryder (17) celebrates a goal, near Edmonton Oilers’ Justin Schultz (19) and goalie Jason LaBarbera (1) during the second period of an NHL hockey game Monday, Oct. 7, 2013, in Edmonton, Alberta. (AP Photo/The Canadian Press, Jason Franson)
August 27th, 2020 at 4:01 pm
I can’t get a signal can buy ventolin over counter france He was wrong to push conservative house members to get the ACA defunding provision put in the bill no matter what, while not having the votes in the senate to pass it that way in addition to knowing it would be vetoed by the president if they did somehow manage to pass what Cruz was pushing. Basically Cruz was asking everyone else to take the political risks of his idealogy, which in case you haven’t noticed is failing.
August 27th, 2020 at 4:02 pm
Another year where can i buy metronidazole Ground source heat pump manufacturer Kensa’s managing director, and chairman of the Ground Source Heat Pump Association, Simon Lomax, said that the “Domestic RHI announcement made today, three and a half years after the initial consultation, is disappointingly short on detail.”
August 27th, 2020 at 4:02 pm
We’d like to offer you the job amoxicilline acide clavulanique biogaran prix “The necessary speed and scope of this transformation, aswell as its critical importance to the future success of thecompany, demand leadership of exceptional skill, agility andvision,” BlackBerry said ahead of its July annual generalmeeting, when shareholders approved the changes.
August 27th, 2020 at 4:02 pm
When can you start? generic cialis uk online pharmacy Andrew Grice has been Political Editor of The Independent since 1998. He was previously Political Editor of The Sunday Times, where he worked for 10 years, and he has been a Westminster-based journalist since 1982. His column, Inside Politics, appears in The Independent each Saturday.
August 27th, 2020 at 4:03 pm
Where’s the nearest cash machine? abchealthfoods.com âThis always stands out in my mind. I remember the Philadelphia game that we played at home,â he recalled of a 10-0 loss on Halloween. âWe stunk up the place in the first half and people threw oranges, tennis balls, toilet tissue, whatever they could throw. They were throwing that stuff at us as we were going in for halftime.
August 27th, 2020 at 4:04 pm
I’ve just graduated where to get legit nolvadex The attack happened the same day the military said thegroup’s bellicose leader Abubakar Shekau might have died betweenJuly 25 and Aug. 4 from gunshot wounds inflicted in a gun battlewith security forces.
August 27th, 2020 at 4:04 pm
Have you got a current driving licence? tretinoin advanced guestbook 2.4 Fortunately, the United States sees through the ruse, with the State Department condemning the resolution for setting “arbitrary deadlines,” which are “more likely to curtail useful negotiations than to bring them to a successful conclusion.”
August 27th, 2020 at 4:04 pm
I can’t stand football buy femigra uk
Although the Festival, its authors, organisers and attendees were putting on a brave face, the situation had taken a turn for the worse. Ghanaian poet Kofi Awoonor, due to perform at an event on Saturday, was uncontactable. His son had been shot in the shoulder in Westlands and had been taken to, and later discharged from, hospital. James Mbugua, a reporter for new Nairobi newspaper The Star, told me that his colleague, a showbiz correspondent, had been killed in the shooting, with another two at the Mall. Speculated statistics came in occasionally: 12 killed, 15 gunmen, 100 trapped in a basement. We later learned that Awoonor had died in the attack.
August 27th, 2020 at 4:06 pm
I do some voluntary work tylenol extra fort A: One of my favourite literary therapists is Thomas Moore,who wrote “Care of the Soul.” One of the things he talks aboutis that sometimes, the soul needs gray - and you simply have toallow the soul its access to gray. You can’t force a haloedcheerfulness on certain subjects and on certain days. And maybethat’s one of the things I do in my work, is that I allow thesoul to access its gray.
August 27th, 2020 at 4:07 pm
I’d like to open a personal account cialis product review Mitchell, the developer and philanthropist who also is considered the father of fracking, doggedly pursued natural gas he and others knew were trapped in wide, thin layers of rock deep underground. Fracking brought an entirely new â and enormous â trove of oil and gas within reach.
August 27th, 2020 at 4:07 pm
I’m on work experience tadalista user review
“When they say ‘Schindler’s list,’ it’s almost like they are using the romance of the original list and the magic of that to sell what was prepared at the end of the war,” said Crowe. “This list is far less valuable.”
August 27th, 2020 at 4:08 pm
I can’t get a signal donde comprarpriligy en usa. He explained that it was a “priority” for Scotland to “secure and monitor an extensive maritime environment” given its geographical position and wealth of offshore and other natural assets.
August 27th, 2020 at 4:08 pm
Is there ? levitra generic levitra âI was totally gobsmacked when I first saw the end result. I had to look about 10 times. I had no idea quite how large I had been and quite how small I am now,” she told SWNS news. “I canât really believe itâs me. My eyes are telling me it is but my head says no.”
August 27th, 2020 at 4:08 pm
I’d like , please accutane cheapest price “The Philippines will shortly enter into consultations and negotiations with the United States on a possible framework agreement that would implement our agreed policy of increased rotational presence,” Gazmin and del Rosario said.
August 27th, 2020 at 4:08 pm
I love this site adverse effect of ibuprofen (advil motrin) in the elderly At least, such is life for Martin Rose (Bana) and Claudia Simmons-Howe (Hall), two lawyers who become ensnared in the legal case surrounding a horrific terror attack, the bombing of a bustling London food market.
August 27th, 2020 at 4:10 pm
Best Site Good Work where to get accutane online David Anderson, an expert in media law at the University of Texas at Austin, said the ruling was consistent with recent rulings in similar cases, which have indicated “a hardening of the judicial arteries toward the press.”
August 27th, 2020 at 4:11 pm
perfect design thanks intrathecal baclofen cost I was laser-focused, though, and this was a new feeling. (I donât know that anyone is laser-focused in life until he or she has a stake in the fate of the outcome.) This wasnât like the quickly dropped interest in the saxophone. I wanted to get good, and I needed to pay my parents back; pride was on the line. I wasnât mindful of creating an authentic brand at this point. I was more focused on whether or not this could be a vehicle to help me get to second base with the opposite sex. But painting quickly became a full-time job outside of school. I came home and hunkered in the garage for seven- to nine-hour stretches, no matter how hot or cold it was.
August 27th, 2020 at 4:11 pm
I enjoy travelling antabuse uk prescription Feig is about to embark on his re-imagining of the 1984 cultcomedy with Melissa McCarthy, Kristen Wiig, Kate McKinnon andLeslie Jones - all part of NBC’s “Saturday Night Live” family -due for release in 2016.
August 27th, 2020 at 4:11 pm
We’d like to invite you for an interview montelukast sodium price walmart The Windows 8.1 tutorials might fare better as they’re placed inside a new application, “Help Tips,” which is visible on the Start screen by default. Placing them in an app both allows the tutorials to be revisitedâWindows 8’s tutorial is only shown on the first log in and can’t readily be replayedâand experienced at the user’s own pace.
August 27th, 2020 at 4:12 pm
A book of First Class stamps zovirax 400 Beijing did not specify then the industries it had in mind,though in 2009 it named nine, including shipbuilding. Industrysources said neither the banking regulator nor any centralgovernment agency had issued new rules on tightening lending toshipyards or other industries.
August 27th, 2020 at 4:12 pm
Could you tell me the dialing code for ? baclofen 20 mg high The upgrade of the class E notes of DTC Eight reflects growth in credit enhancement (CE) levels. Fitch expects the improvement in CE levels to continue and the notes to be repaid at a faster pace than the other rated notes in this transaction, in accordance with transaction agreements.
August 27th, 2020 at 4:13 pm
Where do you come from? cialis diario cadastro The man now living at Ms Taylor’s former address, who was described as a “somewhat confused elderly gentleman”, let Ms Taylor into the house and staff made her comfortable in bed before driving off.
August 27th, 2020 at 4:14 pm
How long are you planning to stay here? what is zenegra 100 Janet Yellen is now the clear front-runner to be nominated as chair of the powerful Federal Reserve. Her status as President Barack Obama’s second choice, while awkward, could ultimately serve as an asset during confirmation and in the central bank’s top job.
August 27th, 2020 at 4:14 pm
One moment, please adcirca dosierung Republican lawmakers, who have not passed budget funding, onThursday offered a plan that would extend the U.S. government’sborrowing authority for several weeks, staving off a defaultthat could otherwise come as soon as Oct. 17.
August 27th, 2020 at 4:15 pm
Can I call you back? premarin tablets coupons “As the consultation on compensation finished last January I am pleased to see the Government move ahead with setting up the safeguarding area so that those living on or near the proposed route can be compensated for the blight they have suffered at the hands of this project
August 27th, 2020 at 4:15 pm
Canada>Canada latisse generic (bimatoprost) 0.03 China’s cabinet last month promised measures such asaccelerating the installation of pollution control equipment onsmall, coal-fuelled refineries and curbing the growth ofindustries such as steel and cement that consume large amountsof energy.
August 27th, 2020 at 4:16 pm
prazosin depression
August 27th, 2020 at 4:17 pm
Have you got any experience? tarasc.com reviews This is very sad but also very unsurprising -_- and the only thing thats going to happen is debate it waste money talking about it try and pitifully doing something find nothing is really changing and go back to square one again. Just like everything else. There really is no hope for man kind if we continue the way we are heading.
August 27th, 2020 at 4:17 pm
I love the theatre penegra does work
Our key players are James Anderson, Prior, Swann and Kevin Pietersen. For me if they stay fit and the team plays near its best then England will win the series. But we should not think everything is perfect in the England camp. It is not. England have two big question marks. Joe Root has done brilliantly for a 22-year-old batting at five or six, coming in against the old ball. But suddenly he has been pushed up to face the much harder new ball which bounces more and always offers some lateral movement. The ball will swing and zip off the turf much quicker at a time when the opening bowlers are fresh. It is going to be a different ball game so do not expect too much from him.
August 27th, 2020 at 4:18 pm
An accountancy practice roidsource.com legit The closed-door session was not included on Obama’s dailypublic schedule for Thursday. It followed another privatesession on Tuesday of Obama administration officials, industrylobbyists and privacy advocates.
August 27th, 2020 at 4:18 pm
I quite like cooking toradol shot for shoulder pain He would surely have been in peril if he’d lost Scotland and his seemingly insouciant attitude to the mechanics of the vote, which nearly proved fatal, has not been forgotten by his Conservative party.
August 27th, 2020 at 4:18 pm
We need someone with qualifications paroxetine 10 mg tablet “A partial deal that leaves Iran with these capabilities is a bad deal,” Netanyahu told Kerry at the start of their meeting in Rome. “You wisely insisted there wouldn’t be a partial deal with Syria. You’re right. If (Syrian President Bashar) Assad had said, ‘Well, I’d like to keep, I don’t know, 20 percent, 50 percent, or 80 percent of my chemical weapons capability,’ you would have refused, and correctly so.”
August 27th, 2020 at 4:19 pm
I’ve got a full-time job ciprofloxacin 750 mg Myriad other factors come into play: lottery funding (for the Olympians and Paralympians), better governing bodies, the oceans of commercial money now sloshing around the upper reaches of professional sport.
August 27th, 2020 at 4:19 pm
How do you do? how to apply himcolin gel In four defined periods of Fed tightening since 1985, all but one - the mid-1990s - preceded a recession. During those times, the Fed raised the fed funds rate by almost 300 basis points, on average. The market’s performance was mixed, while the price-to-earnings ratio of companies in the S&P 500 index declined by 2 percent or a bit more, Price said.
August 27th, 2020 at 4:20 pm
It’s serious flagyl where to buy online Nearly 50 million Americans are on the food stamp program, which has exploded over the last five years, more than doubling the cost to taxpayers. The Electronic Benefits Transfer (EBT) cards are issued to needy citizens who qualify, and then replenished each month with buying power. Because the cards do not include a photo ID, a recipient who is looking to sell his or her benefits for cash can simply do so and then report them stolen or lost and be issued a replacement. They could also charge a buyer much more, and never report the card as missing, effectively transferring their entitlement benefits for cash.
August 27th, 2020 at 4:21 pm
How many more years do you have to go? accutane cream uk At the moment, media attention tends to be negative; Gossip about 70-year-old party founder Oskar Lafontaine’s relationship with 44-year-old lawmaker Sahra Wagenknecht or allegations about Gysi and his wife’s links with the Stasi secret police.
August 27th, 2020 at 4:21 pm
Will I have to work shifts? order priligy dapoxetine Texas - Mack Brown will likely be shown the door with any result short of running the table this year. I am still not sure that a Big XII title can save his job. The Longhorn fan base wants Saban. They won’t get him. If I were running the show in Austin, I think I would take a look and see if Al Golden were interested and available.
August 27th, 2020 at 4:21 pm
Could you ask him to call me? buy levitra from canada Now the Giants not only have Randle (who had 19 catches for 298 yards and three touchdowns last season), but they also have high hopes for Louis Murphy, a speedy 26-year-old who caught 25 passes for 336 yards in Carolina last season. Heâs the fourth receiver in the offense and maybe the fifth option behind tight end Brandon Myers (who caught 79 passes for 806 yards in Oakland last season). But if Randle really does break out this season, Murphy could be the deep threat in the offense that Manningham and Hixon both once were.
August 27th, 2020 at 4:24 pm
How much is a First Class stamp? lisinopril 5mg tab internl lb The panel concluded the little girl’s tragic death, along with at least 18 others citywide between 2005 and 2010, could have been prevented and that “serious errors and shortcomings” are “indicative of the existence of a systemic failure” within the troubled agency.
August 27th, 2020 at 4:24 pm
The United States telmisartan amlodipine combination india Following their first loss of the season to the Houston Astros on Tuesday night, the A’s took the field looking to get back to their winning ways for an early get-away day game on Wednesday. A 4-3 victory on the strength of a pair of homers and solid pitching was good enough to put the A’s back in the win-column and finish the road trip 3-3.
August 27th, 2020 at 4:24 pm
US dollars what is albuterol sulfate syrup Nearly 150 people in the United States died in 2007 and 2008, and hundreds suffered serious reactions, after they were treated with contaminated heparin, according to the U.S. Pharmacopeial Convention, the body that sets standards for drug quality and purity.
August 27th, 2020 at 4:25 pm
I’m doing a masters in law what is nizagara does it work “People have choices. In years to come whether our grandchildren demonstrate respect for each other’s identity and traditions will depend on their relationship with each other; and that will depend on what we, in this generation, do now,” he said.
August 27th, 2020 at 4:25 pm
I work here canadian celebrex online IPOs that could get a bump include a $220 million deal bySeven Convenience Bhd, which could come in the coming months anda $300 million floatation by property development firm IskanderWaterfront early next year.
August 27th, 2020 at 4:25 pm
Stolen credit card trazodone 25 mg high âFirst, the United States would not seek the death penalty for Mr. Snowden should he return to the United States.â In addition, âMr. Snowden will not be tortured. Torture is unlawful in the United States,â Holderâs letter said.
August 27th, 2020 at 4:26 pm
Looking for a job ventolin kopen nederland If consumers submit the required documents by the end of the month, the health agency will help them sign up for a health plan through a special enrollment period, Andy Slavitt, principal deputy administrator at CMS, told reporters in a phone briefing held Monday.
August 27th, 2020 at 4:27 pm
I’m unemployed can you buy tylenol pm under 18
Deen, 66, who had a multimillion-dollar enterprise built on books, restaurants, television shows and housewares, has lost about a dozen business deals after a deposition surfaced last month in which the TV chef admitted to using the “N-word.”
August 27th, 2020 at 4:27 pm
There’s a three month trial period keflex Noemi Meneguzzo, 40, from Vicenza in Italy, was diagnosed with breast cancer in 2007 when she was 34. She had her right breast removed but cancer struck again in 2011 and she is still undergoing chemotherapy. These pictures form part of an exhibition to go on show in October in Turin
August 27th, 2020 at 4:28 pm
A packet of envelopes silagra uk A straightforward brochure mailed to a test group of people, most between ages 60 and 65, stressed the benefits of delaying retirement. Researchers then followed up a year later and compared people who had received the brochure with a control group that had not. They found that many people in the test group – especially women – had decided to keep working.
August 27th, 2020 at 4:28 pm
I work here avanafil wirkungsdauer House Speaker John Boehner, the Ohio Republican leading hisparty’s efforts, will turn down his paycheck, while the Housemajority leader Eric Cantor of Virginia will put his pay asidein escrow until the shutdown is resolved, according to theWashington Post.
August 27th, 2020 at 4:30 pm
real beauty page buy sumatriptan succinate When Martens began looking to join the SEC, he originallyapplied to run its Atlanta office, according to Robert Khuzami,who stepped down as the SEC’s director of enforcement in Januaryand joined Kirkland & Ellis last month.
August 27th, 2020 at 4:31 pm
It’s funny goodluck seroquel mg tablets Fund manager Hargreaves Lansdown, whose website crashed under the volume of “sell” orders on Friday, was forced to suspend the website briefly again yesterday to process the backlog of requests from clients.
August 27th, 2020 at 4:31 pm
I’d like to take the job 170 grand concourse pharmacy The positive ratings for probation services prompted calls for Justice Secretary Chris Grayling to reconsider his promised “rehabilitation revolution”, under which private security firms would be paid to supervise low to medium-level offenders across England and Wales.
August 27th, 2020 at 4:32 pm
Children with disabilities antibiotic tetracycline mouthwash They argue that the nonprofits that run the library - the NYPL, and the Astor, Lenox and Tilden Foundations - are violating the library’s charter which established it as a research facility, not a circulating library.
August 27th, 2020 at 4:32 pm
What do you want to do when you’ve finished? using fluticasone propionate nasal spray while pregnant The Contra Costa County Sheriff’s Office issued a grim advisory Sunday asking residents to “Leave now by car. Go by way of Morgan Territory Road. Take only those essential items you have ready and can carry with you.”
August 27th, 2020 at 4:32 pm
We’ve got a joint account does hydroxyzine pamoate 25 mg get you high That nexus, which has created over 100,000 jobs for Ireland,was laid bare when the U.S. Senate revealed that technologygiant Apple had paid little or no tax on tens ofbillions of dollars in profits channelled through the country.
August 27th, 2020 at 4:33 pm
Yes, I love it! how long does it take for zyrtec to wear off The Senate Gang of Eight legislation, which includes a pathway to citizenship, passed with support from Democrats and Republicans and was pushed by stars of the party like Sen. Marco Rubio, R-Fla., and the 2008 GOP presidential nominee, Sen. John McCain, R-Ariz.
August 27th, 2020 at 4:33 pm
Your cash is being counted findcars With the current Ebola outbreak having a significant economic impact on the country, the Norwegian deal is timely.
August 27th, 2020 at 4:34 pm
Could you give me some smaller notes? buying alesse online With dry understatement he took issue with the bedrock concept of the Joint Strike Fighterâthat a single airplane could fulfill the different missions of three different servicesâcalling it âa little optimistic.â
August 27th, 2020 at 4:35 pm
I’m afraid that number’s ex-directory can you get high off benadryl allergy pills Shock at Ms Halappanavarâs death, and a European judgement criticising Irish law for a lack of clarity, galvanised the government into bringing forward the legislation. In previous abortion controversies the Catholic church and dedicated pro-life groups have prevailed against attempts at legal reform, but this time both public and political opinion was strongly in favour of change.
August 27th, 2020 at 4:35 pm
I study here buy viagra online u
Based on evidence presented openly to the jury and via television to all of America, the six-member jury could just as reasonably have convicted Zimmerman of manslaughter under the extremely convoluted Florida law that defines when a killing is justifiable or excusable. The panelists made the close and defensible call that Zimmermanâs actions were both justifiable and excusable.
August 27th, 2020 at 4:36 pm
What do you want to do when you’ve finished? buy lithium carbonate online uk * UK ECONOMY: Britain’s economy probably expanded faster in the secondquarter than in the first, helped by growing confidence among consumers and bysigns that companies are ready to borrow and spend more.
August 27th, 2020 at 4:37 pm
Where are you calling from? half inderal la 80 mg “United were truly awful at times in the early weeks and months of last season, but the difference between then and now was that they dragged themselves to victories with the late surges that are missing now.
August 27th, 2020 at 4:38 pm
Other amount allopurinol for gout Rouhani, who has asked to meet with French President Francois Hollande on the sidelines of the UN General Assembly new week, said his counterparts should “seize the opportunity presented” by his election.
August 27th, 2020 at 4:39 pm
I’m originally from Dublin but now live in Edinburgh doxycycline buy online australia Recently ousted Egyptian President Mohamed Mursi said lastmonth that “all options” were open in dealing with the issue,prompting Ethiopia to say it was ready to defend its $4.7billion dam, set to be built near its border with Sudan.
August 27th, 2020 at 4:39 pm
Wonderfull great site dosage of misoprostol (cytotec) abortion pill The disturbing revelations stem from a $1.2 million lawsuit filed by Lisa Jackson, a former manager at the Uncle Bubbaâs Oyster House, a Savannah, Ga., restaurant owned by Deen and her brother, Bubba Heirs.
August 27th, 2020 at 4:40 pm
How do you do? caverta opiniones The transit unions in California have claimed that theCalifornia Public Employees’ Pension Reform Act of 2013 (PEPRA)infringes on their right to collective bargaining, resulting inthe Department of Labor not certifying various grants to sevenrated California transit agencies, which affects $3 billion offederal aid and challenging their finances, the ratings agencysaid in a statement.
August 27th, 2020 at 4:40 pm
We’ll need to take up references do you have to wean off crestor According to the Daily Times report, students often stored belongings in the wrestling mats to avoid locker fees. Prine said Johnson had climbed onto the mat to retrieve a shoe that may have fallen into the middle of the stack.
August 27th, 2020 at 4:41 pm
Pleased to meet you generic albuterol hfa “It was the Israeli doctors who cared for her who stepped up and said ‘look, we’re not sending her back,’ and the Israeli court system in the end agreed to that,” Ginsburg said. “They didn’t see her as a Palestinian girl from Gaza. They saw her as a six-year-old girl.”
August 27th, 2020 at 4:41 pm
Go travelling nizoral shampoo online shopping india
Meteor spotting is best when the radiant â the apparent center of the meteor shower, which tonight is Draco’s eyes â is above the horizon. Since Draco the dragon hangs out near the North Star, no one in the Northern Hemisphere needs to worry about losing the radiant tonight.
August 27th, 2020 at 4:41 pm
Yes, I play the guitar serpina1 because he is taking away the revenue I receive in areas that I would use to offset my higher costs in rural areas.”
August 27th, 2020 at 4:42 pm
Where do you come from? how much does depo provera cost at walmart Ireland now has its first law making abortion legal in the country under specific conditions, after President Michael D. Higgins signed the Protection of Life During Pregnancy Bill 2013 into law Tuesday.
August 27th, 2020 at 4:44 pm
magic story very thanks lisinopril for sale uk More than 28 years later, on November 9, 1989, East and West Berliners gathered at the wall to climb over it and dismantle it. The two halves of the city were officially reunited less than a year later, on October 3, 1990.
August 27th, 2020 at 4:46 pm
I want to make a withdrawal lexapro while trying to conceive
But let’s say it does. It may take months before money dribbles in from advertisers. Generally, bloggers set up ads on their site, frequently with mainstream ad players like Google AdSense, Amazon Associates and Pay-Per-Post, all of which are fairly user-friendly. But after finding the advertisers, you’ll need to find readers – a lot of them.
August 27th, 2020 at 4:46 pm
Could you tell me the number for ? cost of wellbutrin xl 150 mg 24 hr In the interview with daily Boersen-Zeitung, CEO MarionHelmes was quoted as saying there was “no urgent need” for analliance or tie-up with any U.S. partner but such a deal couldhelp bulk up purchasing power to get better discounts fromgeneric drugmakers.
August 27th, 2020 at 4:47 pm
Have you got a telephone directory? amoxicillin 500mg time between doses In the capital, cheap mortgages are changing the drivers ofthe market. Big price gains used to be for trophy homes snappedup for cash by super-rich foreign buyers. Now the bidding warsare breaking out in the suburbs.
August 27th, 2020 at 4:48 pm
Another year propranolol hcl 10mg
Charging Snowden criminally is supported particularly by people who think that investigating terrorism trumps privacy; that NSA surveillance enhances U.S. security; that the NSA is not intruding on privacy rights, or if so, is acting justifiably; and that his disclosures have harmed national security. The last gap is the largest: Among those who see no damage to security, just 33 percent support criminal charges against Snowden. But among people who think his disclosures have harmed national security, 71 percent say he should be charged with a crime.
August 27th, 2020 at 4:48 pm
What’s the current interest rate for personal loans? safe order nolvadex online A significant number of the sequences were linked to organisms that live around deep-sea hydrothermal vents, suggesting that such features exist at the bottom of Lake Vostok as well. “Hydrothermal vents could provide sources of energy and nutrients vital for organisms living in the lake,” the researchers said.
August 27th, 2020 at 4:48 pm
The United States cost of terbinafine 250mg tablets
The official policy set by Iran’s first supreme leader, the Ayatollah Ruhollah Khomeini, gives “the expediency of the regime” primacy in conflicts with religious law, Khalaji said. Iran’s religion-based constitution states that education should be free, but for practical reasons the regime charges for college-level education, he said.
August 27th, 2020 at 4:49 pm
Have you got any qualifications? is nugenix available in canada In fact, the first arena tour by the latest teen idol in transition may have been specifically designed to invert such behavior, marketing her as the anti-Miley. “You know what I think is sexy?,” she asked at one point. “Class.”
August 27th, 2020 at 4:49 pm
US dollars indomethacin acute gout Russian investigators said last week they were looking into the possibility that Islamists had shot Nemtsov for defending cartoons of the Prophet Mohammad in French satirical magazine Charlie Hebdo after Islamist gunmen killed 12 people in an attack on its offices on Jan
August 27th, 2020 at 4:49 pm
Do you know each other? probenecid webmd
PMQs was rowdy today – extremely rowdy. The Speaker, John Bercow, gave MPs a ticking off for creating a “wall of noise” and one Labour MP even said it was the “noisiest PMQs I’ve ever known”.
August 27th, 2020 at 4:51 pm
What sort of music do you listen to? diovan cost walmart
The movie benefits from the current cultureâs insistence that every waking moment be documented. When an Elvis impersonator tells a tale of Springsteen pulling him out of the audience to sing with him, thereâs actual footage to prove it. Likewise, when a guy talks about a show where he brought a sign explaining that he just got dumped by the love of his life â which inspired the Boss to invite him up from the orchestra for a very public hug â we get to share in the moment.
August 27th, 2020 at 4:53 pm
I want to make a withdrawal what is quetiapine fumarate 50 mg “It will be cheaper to do your whole genome sequencing thanto get an MRI scan,” said Dr. Christopher Austin, director ofthe National Center for Advancing Translational Sciences. “Whenthat happens, identifying whether a mutation is making you anexceptional responder will be much easier.”
August 27th, 2020 at 4:53 pm
How much is a Second Class stamp? cheap lipitor canada More than a year after Switzer and other residents settled their lawsuit against Cabot Oil & Gas Corp., the rancor has mostly subsided. And Switzer settled on a new approach to the industry that she calls her “landlord.”
August 27th, 2020 at 4:54 pm
What sort of work do you do? cialis for sale 40 mg Senator Edward Markey, a Massachusetts Democrat, said Hagel’s action was “the right decision for the hundreds of thousands of patriots who support our soldiers, and now it’s time to end this harmful government shutdown that has left hundreds of thousands of other federal workers sitting at home.”
August 27th, 2020 at 4:55 pm
I’ve got a part-time job hotel allegra review Matt Labrum, the head coach at Union High School in Roosevelt, Utah, benched all 50 of his players last weekend because of character issues. Fed up with poor grades, attendance and attitude problems, in addition to learning that one or two players may have been involved in cyber-bullying another student, Labrum ordered all of his players to turn in their jerseys and equipment following a loss to Judge Memorial Catholic on Sept. 20.
August 27th, 2020 at 4:55 pm
We used to work together fluticasone furoate He added: “I’m determined that as the economy recovers we don’t leave behind a whole group of people on long-term unemployment and wash our hands of them. That’s what’s happened in the past, I don’t want that to happen on my watch.”
August 27th, 2020 at 4:55 pm
Do you know each other? cuanto cuesta el tamoxifeno Kenyatta’s focus on Kenya’s troubles, and of his role in a global campaign against terrorism, was a reminder that he faces trial at The Hague in a few weeks time for crimes against humanity over violence that followed a 2007 election.
August 27th, 2020 at 4:55 pm
I’d like to pay this in, please imitrex tabs 9’s Mr Sarjantson, and his partner, Tracy Alexandra, who witnessed the attack and now cares for him, sued the Chief Constable of Humberside, claiming that the delay in responding to the call amounted to a breach of the European Convention on Human Rights.
August 27th, 2020 at 4:56 pm
Sorry, I ran out of credit fluticasone furoate aqueous nasal spray “Our forces are combing the mall floor by floor looking foranyone left behind. We believe all hostages have been released,”the Ministry of Interior said on Twitter early on Tuesday,adding his forces were “in control” of the building.
August 27th, 2020 at 4:57 pm
I’m sorry, I didn’t catch your name adalat oros 60 para que sirve “The United Nations is engaging with a wide range of parties within Syria,” Stephane Dujarric, a U.N
August 27th, 2020 at 4:58 pm
What’s the last date I can post this to to arrive in time for Christmas? order propecia uk The following year, Holder authorized the Justice Departmentto issue a subpoena seeking Risen’s testimony. Risen challengedthe subpoena, saying he could not be compelled to testify underthe First Amendment and federal common law.
August 27th, 2020 at 4:59 pm
Excellent work, Nice Design como comprar viagra en estados unidos
Negotiators are due to convene with little fanfare later on Wednesday in Jerusalem, the holy city at the heart of the decades-old conflict of turf and faith. The envoys held first talks in Washington last month, ending a three-year stand-off.
August 27th, 2020 at 5:00 pm
The United States venlafaxine price canada “Yeah, I’m sure. I mean, it’s like he’s in a world and he feels scared – sort of like myself. I’ve had a slightly complicated life and I fear… It’s like he’s got the mark of Cain on him. It makes him recognisable all over the world. Anybody who feels that they’re under any type of a cloud or anything like that, I think this is what he feels. I can sort of relate to losing his sense of peace, losing his sense of joy. I’ve lost people in my life. I cremated my friend last week, my best friend of 21 years. That creates a pain that can never be quenched.”
August 27th, 2020 at 5:01 pm
I came here to study buy generic amoxil online This ultralight composite material also has the benefit of failing only incrementally, as opposed to the large scale failings of traditional composite materials. “It’s a massively redundant system,” posited Gershenfeld.
August 27th, 2020 at 5:01 pm
Thanks funny site lamictal tablets Moody’s Analytics, another leading economics consulting firm, estimates that 1 million of the 2.7 million jobs gained in the U.S. between 2002 and 2012 were related to shale oil and gas drilling, Moody’s economist Chris Lafakis said.
August 27th, 2020 at 5:01 pm
Where do you study? buy nexium esomeprazole Richards has seven years at an annual cap hit of $6.67 million. The Rangers’ decision to keep him severely limits their ability to upgrade their team in free agency, which opens on Friday. They have about $13 million available to re-sign restricted free agents Ryan McDonagh, Derek Stepan, Carl Hagelin and Mats Zuccarello before even addressing the open market.
August 27th, 2020 at 5:02 pm
I’d like to change some money best place to buy genuine viagra
Donât even bother asking for a Bud Light at New Yorkâs newest beer hall. Because when Clinton Hall opens in the Financial District Monday, there wonât be a mass market brew in sight. Not even a Sam Adams.
August 27th, 2020 at 5:02 pm
I’ll put him on himcolin gel bangladesh Financial markets have given Tokyo the benefit of the doubt:the government can borrow 10-year money for less than 0.7percent. But government officials and private economists havelong feared a crisis in confidence in Japan’s creditworthinessthat could cause a crippling spike in interest rates.
August 27th, 2020 at 5:02 pm
I came here to work betamethasone clotrimazole gentamicin triderm ointment Armed with a federal death law, the Brooklyn U.S. attorneyâs office took up the case . Prosecutors won a conviction at the end of 2006, and the jury took up the question of life or death. Wilson admitted guilt and pleaded for mercy. His lawyers presented evidence that he was the product of hard, cruel conditions. The jury called for sending him to his grave.
August 27th, 2020 at 5:03 pm
I’ve been cut off diclofenac non prescription uk “Timeline views,” a measure of how many times a userrefreshes his or her stream of tweets, grew 10.7 percent in thesecond quarter to almost 151 billion, and 16.1 percent to 136.3billion in the first.
August 27th, 2020 at 5:05 pm
I’d like to withdraw $100, please latisse careprost amazon “We knew that corals have cilia, but did not expect that they could produce flows that are so violent.”
August 27th, 2020 at 5:05 pm
I’ll call back later viagra daily use “At the end of the day you can’t sit back and judge a man based on a bad year or whatever you want to call it,” Coples went on. “He’s still a great coach, and we’re looking forward to getting better and he’s looking forward to preparing us and making sure we getbetter as well.”
August 27th, 2020 at 5:05 pm
It’s OK 500 mg amoxicillin dosage for sinus infection “Although these measures are effective, they aren’t fail-proof and people don’t always use them. We need to move to a broader approach to tick reduction, involving entire communities, to combat this public health problem,” said Lyle Peterson, director of the CDC’s Division of Vector-Borne Diseases, in a press release.
August 27th, 2020 at 5:07 pm
I’d like to send this to how long can you be off coumadin “It’s a bold step into the future — a win-win for employees, shareholders and consumers of both companies,” Microsoft CEO Steven Ballmer told reporters at Nokia’s headquarters in Finland Tuesday. “It’s a signature event.”
August 27th, 2020 at 5:07 pm
I’d like to transfer some money to this account ibuprofen 400 mg dosage for adults All 200 House Democrats were invited to the afternoon session at the White House, and Democratic leaders said most made the trek. They said Obama was resolute about not negotiating with Republicans until they drop their demands.
August 27th, 2020 at 5:08 pm
Special Delivery cialis daily 5mg online “There’s all kinds of consulting opportunities,” said Levin,whose client, the Detroit Institute of Arts museum, is at thecenter of a dispute over whether the city can sell the museum’sart collection.
August 27th, 2020 at 5:09 pm
Who would I report to? gnc arginmax canada Some U.S. lawmakers have called for a halt to the $1.5 billion a year given mostly in military assistance to Egypt to bolster its 1979 peace treaty with Israel. Military cooperation includes privileged U.S. access to the Suez Canal.
August 27th, 2020 at 5:09 pm
I don’t like pubs amoxicillin/clav 875/125 mg While the lean microbiome appeared to dominate when the diet was healthy, cohabitation didn’t help obesity-prone mice that were given a diet high in fat and low in plant matter. When the mice that got transplants from obese twins ate like typical Americans, there was no evidence that the organisms from their lean housemates were becoming established in their guts.
August 27th, 2020 at 5:09 pm
Lost credit card where can i buy flagyl uk While ceding ground on re-tendering, it confirmed a draftrecommendation that the FRC should review the audit engagementfor each of the 350 companies on average every five years, aheavy undertaking for the regulator.
August 27th, 2020 at 5:09 pm
The United States strattera 10 mgs “I was ready to celebrate my new birth,” he continued. “But when I looked in the mirror, I was disgusted with myself. My new breasts did not match my expectations and my new penis had symptoms of rejection. I do not want to be … a monster.”
August 27th, 2020 at 5:10 pm
In tens, please (ten pound notes) price of aravana in sabarimala Why then does this movement exist at all? And how did it spread to hundreds of college campuses? (Ah, the beauty of electronics and social media.) Well, to raise “awareness,” of course. Or, more specifically, to satisfy the organizers’ desire to bask in moral superiority and gloat about heroically “fighting” “evil.” Instead of having to stop using their iPads and Macbooks, they find symbolic gestures to mute their cognitive dissonance without having to change those very pleasurable behaviors.
August 27th, 2020 at 5:11 pm
Can I take your number? where can i buy zyrexin in the uk The Scotsman provides news, events and sport features from the Edinburgh area. For the best up to date information relating to Edinburgh and the surrounding areas visit us at The Scotsman regularly or bookmark this page.
August 27th, 2020 at 5:12 pm
We need someone with qualifications bula do naprosyn 500mg âThereâs an outside chance,â Lukas continued about entering Oxbow . âIâm not really pushing for it. Weâll have to give it a couple of weeks and see. Iâm looking more towards the Breedersâ Cup on (Nov. 2).â
August 27th, 2020 at 5:13 pm
Can you hear me OK? elavil online pharmacy Deadline reported, however, that the spec script by “The Way Back’s” Keith Clarke hews considerably closer to the novel that follows the titular Jewish prince and his childhood-friend-turned-enemy Messala, whose feud builds towards the story’s signature chariot race.
August 27th, 2020 at 5:14 pm
I’ve got a part-time job sinrex australia
Hanan Ashrawi, a Palestinian spokeswoman, told AP the upcoming talks are being held under more difficult conditions than previous negotiations. Specifically, Ashrawi cited the Palestinian political split, with Western-backed moderates and Islamic militants running rival governments, and the more hawkish positions of Israel’s prime minister, Benjamin Netanyahu, compared to his predecessor.
August 27th, 2020 at 5:16 pm
I’m not interested in football doxycycline hyclate 100mg sale Much of the legal wrangling over whether Guandique will receive a new trial has taken place out of the public eye, but even Levyâs parents have expressed doubts about whether the right man was convicted.
August 27th, 2020 at 5:16 pm
Have you got any qualifications? viswiss effectiveness The popular facility, which can handle up to 1,000 customers at a time, also has a restaurant, whirlpool, sauna and lavish play area for young children, including girls who are allowed to mix with the opposite sex until the age of about 10.
August 27th, 2020 at 5:17 pm
I’m sorry, I didn’t catch your name seroquel 12.5mg for sleep Instead, Del Raye began by observing a captive great white at the Monterey Bay Aquarium, measuring its downward drift as it coasted through its tank. Because this shark has a carefully regulated diet, Del Raye could calculate how its buoyancy changed with time after feeding.
August 27th, 2020 at 5:17 pm
I can’t get a dialling tone advanced pharmacy solutions genoa Polgar and her two sisters - Zsuzsa (Susan) and Zsofia(Sofia) - won the 1988 Chess Olympiad for Hungary’s female team,ending Soviet dominance. Judit Polgar joined men’s tournamentsand became one of the top players in the world, demolishing themyth that chess is the mental sport of smart men.
August 27th, 2020 at 5:17 pm
Good crew it’s cool buy differin 3 gel online LONDON, Sept 24 (Reuters) - European shares crept up onTuesday as merger and acquisition activity in the telecomssector outweighed downbeat U.S. and German data and a drop inprofits for cruise operator Carnival.
buy differin 3 gel online LONDON, Sept 24 (Reuters) - European shares crept up onTuesday as merger and acquisition activity in the telecomssector outweighed downbeat U.S. and German data and a drop inprofits for cruise operator Carnival.
August 27th, 2020 at 5:17 pm
A packet of envelopes supreme lx cream artistry âThatâs all people ever talk about,â Jacobs said. âYou sit down to eat at a restaurant and people say, âHey you, I got you on my fantasy team, you gotta do something for me.â Come on, Iâm trying to enjoy my dinner.
August 27th, 2020 at 5:18 pm
I like it a lot 502bar.com Oil prices have been dropping amid concerns that a prolongedU.S. government shutdown would hurt demand, but the losses werelimited as the storm in the Gulf curbed supply. Brent futures fell below $109 a barrel, then edged back up above thatmark on Friday.
August 27th, 2020 at 5:19 pm
Could I make an appointment to see ? buy fluconazole uk
Scientists have learned a lot about Ãtzi the Iceman since discovering him in a melting glacier in the Ãtztal Alps back in 1991. He had brown eyes, bad teeth, a lactose intolerance, a predisposition to coronary heart disease and Lyme disease (most likely), according to Discovery News.
August 27th, 2020 at 5:20 pm
Do you have any exams coming up? meloxicam metacam Rouhani, who has vowed that Iran will be more transparent and less confrontational in talks both with the IAEA and the big powers, said this week that time for resolving Iran’s nuclear dispute with the West was limited.
August 27th, 2020 at 5:21 pm
Sorry, I’m busy at the moment buy viagra sample About 30 minutes later they stopped and got out because Zahid Ullah, an Afghan National Army soldier, found something dangerous and potentially deadly in a cemetery nearby â a homemade pressure plate. It was expertly constructed â two pieces of plywood with springs between them connected to wires and wrapped in yellow tape.
August 27th, 2020 at 5:21 pm
I’ve got a very weak signal is protonix available without a prescription “Europe needs a kick-start and today the Commission isapplying the jump leads,” Commission President Jean-ClaudeJuncker, a conservative former prime minister of Luxembourg whotook office this month, told the European Parliament.
August 27th, 2020 at 5:23 pm
Sorry, I ran out of credit priceline pharmacy dfo cairns Though the film plays like late-era Woody Allen â not necessarily a good thing â and Goldbergâs rambunctiousness is more annoying than liberating, thereâs a serious depth of feeling here. Bosworth, thankfully, is attuned to that, and makes the most of it.
August 27th, 2020 at 5:24 pm
How many are there in a book? how to buy celebrex online Such civility officially ended in the last year of Carter’s administration, however. In 1980, Attorney General Benjamin Civiletti issued a legal opinion, based on the 1884 Antideficiency Act, that forbade government operations if Congress hadn’t agreed to fund them.
August 27th, 2020 at 5:24 pm
Could you send me an application form? suprax 100 mg suspension In the photo, Bush is seated in a wheelchair, a stack of papers on his lap and his left hand poised with a pen. One bright red sock and one bright blue one peek out below the cuffs of his blue slacks.
August 27th, 2020 at 5:24 pm
We used to work together ultimatemedgroup.com The July announcement by Publicis Groupe of France and Omnicom Group Inc. of the U.S. that they would form the world’s largest ad firm through a $35 billion merger has sparked a debate over whether the industry needs further consolidation.
August 27th, 2020 at 5:24 pm
I’d like to apply for this job does synthroid help you get pregnant From January to June, the total number of foreign visitors, including business travelers and residents, entering China declined by five per cent to just under 13 million compared with the same period last year, according to the China National Tourism Administration. Overall, visitors from Asia, Australia, Europe and the Americas all declined.
August 27th, 2020 at 5:24 pm
Yes, I play the guitar en que capitulo de alma pirata se besan allegra y benicio “Bernanke’s statements following the release of the minutesprovided confidence after he reassured that the Fed won’tautomatically increase interest rates after the unemploymenttarget rate is reached,” said Miguel Audencial, sales trader atCMC Markets, in a note.
August 27th, 2020 at 5:24 pm
Will I get paid for overtime? clindamycin phosphate for boils The Daily News has some of the most memorable photos in sports history. From legendary boxers and iconic tennis players to golfing greats and fabled Olympians, the Daily News has the photos you want of the once-in-a-lifetime sports moments. Find yours today and relive history.
August 27th, 2020 at 5:26 pm
An envelope 5mg cialis price But Little reiterated the U.S. contention that Syrian President Bashar al-Assad’s forces were responsible for the attack and he dismissed the possibility rebels could have done it. Little said more than 30 countries blame Syrian government forces.
August 27th, 2020 at 5:27 pm
Best Site good looking kamagra online paypal uk Sinatra died in 1998 at age 82. The singer’s daughter, Nancy Sinatra Jr., when asked about the family’s relationship with Ronan, told the magazine in an email, “He is a big part of us, and we are blessed to have him in our lives.”
August 27th, 2020 at 5:28 pm
A company car best place buy proscar online NOTES: Ian Kinsler set a Rangers’ record with his 162nd career steal, breaking a tie with Bump Wills. … Detroit’s Victor Martinez left the bases loaded with a third-inning strikeout and had his hitting streak snapped at 14 games. … Tigers ace Justin Verlander (9-6) starts Sunday against Texas LHP Martin Perez (3-1).
August 27th, 2020 at 5:30 pm
Could you tell me the dialing code for ? overdose on oxcarbazepine However, this is a myth, the researchers insisted, and in fact, people who smoke tend to crave more fatty foods than non-smokers.
August 27th, 2020 at 5:30 pm
Jonny was here weaning off claritin-d The encryption is supposed to prevent the authentication code being discovered, but Mr Nohl said that in about half of these cases it was based on a 1970s coding system called Digital Encryption Standard (DES), which was once thought secure but could now be cracked “within two minutes on a standard computer”.
August 27th, 2020 at 5:30 pm
I can’t get a signal neurontin negative reviews
The Tea Party is not a movement, it is a cult or a sect, a subset of a religion. And while they may not go away, they could be muted if the Speaker had even the slightest amount of courage or honor. They are a minority within their party, and can’t elect one of their own to lead the party. They can be snuffed out, like McCarthyism, when Republican leadership (if such a thing exists) acts responsibly.
August 27th, 2020 at 5:31 pm
I’m sorry, I didn’t catch your name avodart and getting pregnant Our key players are James Anderson, Prior, Swann and Kevin Pietersen. For me if they stay fit and the team plays near its best then England will win the series. But we should not think everything is perfect in the England camp. It is not. England have two big question marks. Joe Root has done brilliantly for a 22-year-old batting at five or six, coming in against the old ball. But suddenly he has been pushed up to face the much harder new ball which bounces more and always offers some lateral movement. The ball will swing and zip off the turf much quicker at a time when the opening bowlers are fresh. It is going to be a different ball game so do not expect too much from him.
August 27th, 2020 at 5:31 pm
We were at school together order amoxicillin online overnight Researchers are now adapting the same platform for use with other paediatric health issues, including rheumatism, neurological and neuromuscular diseases, and obesity… for the sake of other children all around Europe.
August 27th, 2020 at 5:31 pm
A packet of envelopes prescription drugs starting with v Today’s ruling also opens up a new avenue for charging leakers and whistleblowers—section (a)(1) of the Computer Fraud and Abuse Act, which until now, has never led to a conviction. It’s was crafted in the 1990s by taking some of the worst parts of the Espionage Act and adding the phrase “with a computer.”
August 27th, 2020 at 5:32 pm
No, I’m not particularly sporty order cialis online dream pharmaceutical The products appeal to consumers in part because of manufacturers’ claims that they can be conveniently flushed down the toilet. But their cloth-like material doesn’t break down in the sanitary sewer system like toilet paper and can block sewer lines, clog equipment and increase cities’ maintenance and repair costs.
August 27th, 2020 at 5:32 pm
Best Site good looking mexitil 200 mg kaufen
Carl Bridenbaugh, FirstEnergy vice president of transmission who was the director of transmission, planning and system protections at the time, said “you can never say never” about the chances of such a power failure again. Bridenbaugh is one of those who describes the crisis as “the event.”
August 27th, 2020 at 5:32 pm
The manager vigrx uk This police recording offers a glimpse of the criminalunderbelly of trade between the European Union and China, whosemind-boggling size - worth well over 1 billion euros a day -makes it fiendishly hard to police. Making matters worse, the EUis a single market of 300 million people but which has 28national customs authorities with differing priorities.
August 27th, 2020 at 5:34 pm
Best Site Good Work buy depakote Action memo can “read” your scrawling handwritten addresses, e-mail addresses, and the like, and drop them into an address book, onto a map, or stick a URL into a browser. Accuracy seemed pretty good in my tests, and I’ve been known to produce some pretty bad chicken scratch. The other shortcuts were equally good at doing what they say with lassoing items for the scrapbook, saving screenshots of pages you can immediately annotate, and my favorite: initiating the universal search.
August 27th, 2020 at 5:36 pm
Is there ? clonidine for restless leg syndrome Trading was expected to remain subdued ahead of FederalReserve Chairman Ben Bernanke’s testimony on Wednesday beforethe House Financial Services Committee. His comments will beclosely analyzed for signs of when the central bank may startreducing its stimulus efforts.
August 27th, 2020 at 5:36 pm
Could you ask him to call me? prednisone buy online uk Water authority General Manager Pat Mulroy recently made headlines when she said the drought on the Colorado was a natural disaster no different than Hurricane Sandy â and every bit as deserving of federal aid.
August 27th, 2020 at 5:37 pm
Who would I report to? viagra cialis online trial pack The Health Insurance Marketplace, the centerpiece of the 2010 Affordable Care Act (more commonly known as “Obamacare”), is set to launch two weeks from today — on October 1. This online insurance exchange is designed to help millions of previously uninsured Americans obtain affordable health care coverage.
August 27th, 2020 at 5:38 pm
Can I call you back? diurex water pills coupons He said that would still be “negative”, but that he believed it would be less damaging now because financial markets were much more confident than they had been in recent years.
August 27th, 2020 at 5:38 pm
What do you do for a living? aarp viagra discount Yields on the benchmark 10-year note were hovering at 2.624percent, making a fall of roughly 25 basis pointssince last week’s shock decision by the Federal Reserve tomaintain its asset buying programme for now.
August 27th, 2020 at 5:38 pm
I like watching TV astrazeneca seroquel sales Bold moves matter more than ever this season thanks to a new twist: The Mastersâ sous chefs will compete online in âBattle of the Sous Chefs.â Their performances could make or break their Mastersâ advancement â giving them either immunity or penalties during cooking challenges.
August 27th, 2020 at 5:38 pm
Thanks funny site valacyclovir buy online uk “We show consequences to the violence, unlike some of thesePG-13 blood-less movies you see this summer … We’re dealingwith those consequences in a somewhat realistic fashion, to bothmine drama but also comedy,” he said.
August 27th, 2020 at 5:39 pm
What line of work are you in? buy rogaine for eyebrows This comes from our ad serving technology and is used to track how many times you have seen a particular ad on our sites, so that you don’t just see one advert but an even spread. This information is not used by us for any other type of audience recording or monitoring.
August 27th, 2020 at 5:39 pm
Do you know the address? take clomid to have twins In February, Leon scolded IBM for a “history” of violatingprovisions of the Foreign Corrupt Practices Act and “majorpayments” to foreign governments, the latest federal judge toexpress concerns over U.S. regulators’ handling of settlementswith corporations during the past two years.
August 27th, 2020 at 5:40 pm
Very Good Site dulcolax laxatives reviews No doubt they all had more important matters to attend to. Such as squaring the costly loss with Excalibur’s backers, perhaps – the New York hedge fund Platinum, US litigation funding specialist BlackRobe, and the shipping tycoons Andonis and Filippos Lemos.
August 27th, 2020 at 5:42 pm
Incorrect PIN where to buy levothyroxine online Call me a fogey, but I’m growing thoroughly fed up with the whole ‘Gap Yah’ cult, which is to be witnessed at its very worst at Britain’s boarding schools. I try and take an interest when sixth-formers tell me of their exciting Gap Year plans – ‘helping’ African villagers, bungee-jumping from the Niagara Falls, becoming a gaucho in Patagonia – but it’s becoming hard to stifle a yawn.
August 27th, 2020 at 5:42 pm
Can I use your phone? hghup applied nutriceuticals The scientists focused on August, as it is the most active month for wildfires in the American West, analyzing current and forecasted climate patterns in a mountainous region covering Arizona, Idaho, Nevada, New Mexico, Utah, and Wyoming. In August 2012, 3.6 million acres were scorched by 6,948 wildfires in the mountainous region â the largest since August 2000. While the number of wildfires was the second fewest in the 12-year period covered by the study, the wildfires were physically much larger.
August 27th, 2020 at 5:43 pm
It’s OK does paxil cause you to gain weight Icahn, who with 8.9 percent of the company is now its second-largest shareholder, has said little about what future he envisions for the company beyond that it has promising prospects based on its large base of PC customers, and that it should remain partly public.
August 27th, 2020 at 5:44 pm
The United States buy cheap generic valtrex
BTW, is death by CW worse than death by bombs or drones? Limbs blown off, and watching your self die. Children too. I don’t think we are in any position to be too judgmental. Of course, I am against the bombing of Syria, and the drones, and the use of CW.
August 27th, 2020 at 5:45 pm
In tens, please (ten pound notes) voltaren injection side effects Nevertheless, the regulations, or the threat of them, have had a major effect on the for-profit sector. Enrollment was down 2.8 percent in 2011, compared to a .2 percent drop in higher education overall. Apollo Group, which runs the University of Phoenix, noted a 14 percent drop in enrollment between summers 2011 and 2012, and its stock is down 80 percent from its 2009 high. Industry watchers attribute this partly to a rebounding economy, but also to new orientation programs in various schools that let students take classes tuition-free for a trial period, so that if they drop out they wonât incur debt and hurt the collegeâs default rates. That type of screening has led to lower enrollment.
August 27th, 2020 at 5:45 pm
I’m doing an internship glycomet trio 1 price But amid the fervor over gun sales, which have jumped by an estimated 20 percent at Cabela’s over the last 12 months, analysts and fund managers cite another reason for the company’s success: its use of customer data. And they say this should allow the shares to rise further when the overall growth in firearm sales slips.
August 27th, 2020 at 5:45 pm
perfect design thanks what is remeron 15 mg used for “This agreement provides further proof that the Government’s new franchising schedule is on track, delivering value for money for the taxpayer and supporting the ongoing multibillion-pound investment programme in our railways.”
August 27th, 2020 at 5:46 pm
How much will it cost to send this letter to ? baclofen 10 mg tablet para que sirve Part of the Maluku chain, formerly known as the Spice Islands, the area is about 400 miles north of Australia, and hosts small kangaroos and rare birds of paradise with dazzling bright feathers.
August 27th, 2020 at 5:46 pm
My battery’s about to run out vigora 100 red pill There was a common expat theme among a number of my travelling companions who, having settled in a country away from their own, used their new home as a base for their blogging and proving that some of the most popular and readable content on the internet comes from those that seek to carve out a life overseas.
August 27th, 2020 at 5:47 pm
Good crew it’s cool apcalis generic viagra The 26-year-old mother said they wanted to go to Kiribati because âwe didnât want to go anywhere big.â She said they understood the island to be âone of the least developed countries in the world.â
apcalis generic viagra The 26-year-old mother said they wanted to go to Kiribati because âwe didnât want to go anywhere big.â She said they understood the island to be âone of the least developed countries in the world.â
August 27th, 2020 at 5:48 pm
I’ve got a full-time job viagra online kaufen empfehlung
Another grading program is Certified Angus Beef, a designation awarded by the Wooster, Ohio-based Certified Angus Beef brand, which was created in 1978 in order to supply consumers with high-quality meat. Angus is a breed of cattle, so just because something is labeled “Angus” doesn’t mean it has passed any sort of quality control. In order to earn the brand’s logo, qualifying beef must pass eight specifications more than USDA Choice regarding marbling, tenderness and consistency of flavor. Tellingly, only one in four Angus in the U.S. qualify.
August 27th, 2020 at 5:48 pm
How do you spell that? allegra 24 hour wears off An anaesthetist stood by during the op at Epsom Hospital, Surrey, but he was not needed. Surgeon Dominic Neilson said: “It certainly was a bit nerve-racking making the first cut but once we got through that bit it became like doing any other ankle replacement.”
August 27th, 2020 at 5:49 pm
I’m a housewife rhinocort fiyat But supporting U.S. oil prices, the U.S. Energy InformationAdministration slightly tightened its outlook for oil markets in2014, but left the balance for 2013 unchanged, according to areport released on Tuesday.
August 27th, 2020 at 5:51 pm
I’m sorry, she’s effexor xr 150 generic But few takeover attempts are successful. When Putney Park, a girls’ school that occupied four Edwardian houses in south-west London, announced in February that it would close this summer, parents launched a rescue mission. “Everybody said, ‘We’ll fight to save the school,’ but they were all looking for another place for their child at the same time,” says Audrey Pakenham-Money, whose 11-year-old daughter, Isabella, would have started at the school this week. “The school left it late to tell parents who, quite rightly, thought of their own child first. If they got a place at another school, they took it.”
August 27th, 2020 at 5:51 pm
I’ll call back later clenbuterol and anavar cycle results But even if Health Management’s stock pulled back to $15 a share from current trading levels, the company still would be an expensive purchase for Community and might not generate enough cost savings to justify a deal, Skolnick said.
August 27th, 2020 at 5:52 pm
I can’t get through at the moment zithromax taken off market Since then the government has called for major investment tomodernise the network and harness new renewable energy sources.At the same time the energy regulator has offered attractivereturns and regulations to encourage development.
August 27th, 2020 at 5:53 pm
A book of First Class stamps what is caverta tablet “Vivendi’s transformation is on track,” Fourtou was quotedas saying. “I have said and continue to say that I will leaveonce a split of Vivendi has been completed. Vincent Bollorecould replace me as chairman of the media branch … I will helphim.”
August 27th, 2020 at 5:53 pm
Where are you calling from? cymbalta official site Sarkozy has immunity for life for any official acts carried out while he was president, but would suffer if investigations lead to charges against people in his inner circle or if he is found to be at fault over his 2007 campaign funding.
August 27th, 2020 at 5:54 pm
No, I’m not particularly sporty clotrimazole 200 mg suppository Looking to upstage her father’s fame, Bono’s daughter Eve Hewson showed up to the Cannes Film Festival to showcase her own stardom. The 19-year-old actress flew to the South of France to promote her new film ‘This Must Be The Place.’ To top it off, she stars in the film alongside Sean Penn.
August 27th, 2020 at 5:54 pm
I’d like to tell you about a change of address can you get high off of zyrtec Hundreds of federal firefighters fought the blaze, battlingflames door to door with support from water-dropping helicoptersand airplane tankers. By the time it was over, the so-calledBeaver Creek blaze had blackened 112,000 acres (45,300 hectares)of tinder-dry pine forests and sagebrush flats.
August 27th, 2020 at 5:54 pm
I’m a trainee by zyban online Gold’s advance was halted as the dollar’s strength pared themetal’s allure as an alternative investment
August 27th, 2020 at 5:54 pm
I’m on holiday buy fosamax plus d “ADP clearly confirms the U.S. job engine is operating onall cylinders, slanting the odds toward, or at least putting thepressure on the Fed to taper sooner rather than later,” saidBoris Schlossberg, managing director at BK Asset Management inNew York.
August 27th, 2020 at 5:55 pm
Three years actos 30 mg 28 film tablet âWe won,â said Rivera, who retired all four batters he faced to silence the Oâs. âThatâs what we want and thatâs what counts. I have to be ready for that situation. It sounds like a broken record, but thatâs where it is.â
August 27th, 2020 at 5:56 pm
this post is fantastic zyban prescriptin uk “It seems like the Fed is raising the bar on a future rate hike. For the moment, the dollar is likely to trade in itsrecent range until there is a clear signal from the Fed,” saidKatsunori Kitakura, associate general manager of market makingunit at Sumitomo Mitsui Trust Bank in Tokyo.
August 27th, 2020 at 5:57 pm
I’m in my first year at university coreg 25 mg tablets Pharmaceutical company Bristol-Myers Squibb said inU.S. Securities and Exchange Commission (SEC) filings that ithad favourable tax rates in Ireland and Puerto Rico under grantsnot scheduled to expire before 2023.
August 27th, 2020 at 5:58 pm
I’m sorry, she’s kaiser santa teresa 1 north pharmacy hours “Our overall gross margin has been impacted by a relativelyhigher cost structure, lack of economy of scale and certainprovisions needed to facilitate the clearance of agingproducts,” it said in a statement.
August 27th, 2020 at 6:00 pm
We need someone with experience can zoloft pills be split “We were all happy when this court case started because we thought it was an effort to clean up the Deep State. But we soon realised it was an effort to clean up political opponents,” said Nedim Sener, an investigative journalist accused of links to Ergenekon and still on trial in a related case.
August 27th, 2020 at 6:00 pm
I support Manchester United retail price for amoxicillin
It does not conduct its own original research nor does it monitor climate related data but assesses the most recently available information about climate change. It draws on peer-reviewed studies and published scientific works.
August 27th, 2020 at 6:00 pm
I’m interested in order viagra soft tablets I haven’t seen a single smartwatch yet that I’d describe as slim and elegant, but Qualcomm has done a respectable job of keeping the Toq from being too completely ungainly. After seeing the Toq in person, I can tell you that it’s large but not too chunky.
August 27th, 2020 at 6:01 pm
I’d like a phonecard, please can you get a yeast infection from keflex If he can keep it going through the weekend, he might take a run at Julius Boros, the oldest major champion in golf history when he won the PGA Championship at age 48. Heck, Tom Watson nearly won this tournament a few years ago at age 59.
August 27th, 2020 at 6:02 pm
Where’s the nearest cash machine? much does clomid treatment cost uk “This decision puts us a step closer to finishing the investigation,” Nelson said in a statement. “Nothing can bring these boys back but I’m hopeful that their families will now get the closure they deserve.”
August 27th, 2020 at 6:03 pm
Good crew it’s cool is trazodone used for pain “Washington can learn a lot from organizations like Point of Light,” Nunn said
is trazodone used for pain “Washington can learn a lot from organizations like Point of Light,” Nunn said
August 27th, 2020 at 6:03 pm
I’d like to change some money risperidone .25 mg tablets Preheat the oven to 200C/gas mark 6. Line a small, deep tray with baking parchment, pour in the caster sugar and heat it in the oven until the sugar is just beginning to melt at the edges. Heating the sugar helps to create a glossy, stable mixture. Pour the egg whites into a mixer and whisk them slowly, allowing small stabilising bubbles to form, then increase the speed until the egg whites form stiff peaks.
August 27th, 2020 at 6:04 pm
How much is a Second Class stamp? paxil cr 12.5 generic
Dr Johnson, 55, who works as a freelance historian, said: âWe were overjoyed when it was confirmed that we had found the remains of Richard but this has quickly turned sour, largely due to the actions of the university.
August 27th, 2020 at 6:07 pm
I study here amitriptyline pill image
The woman who testified on Tuesday had been a 24-year-old graduate student at the University of California at Berkeley in December 1961, when she met Naso at a bus stop. He offered to drive her home, and the first time he did just that, she testified.
August 27th, 2020 at 6:07 pm
Could I make an appointment to see ? micardis discount coupon The episode is a hotly contested one. In evidence to the Francis inquiry into care at Stafford hospital it was claimed that Lady Young disbanded the CQC’s national investigations team because it was being used to “bayonet the wounded on the battlefield”.
August 27th, 2020 at 6:08 pm
I’ve lost my bank card import cialis into australia Merkel held preliminary talks last week with the SPD, who have 193 seats, and the Greens, on 63. Neither seems desperate to join Merkel, whose last partners, the Free Democrats, failed to get into parliament for the first time since 1949.
August 27th, 2020 at 6:08 pm
Can you hear me OK? where can you buy permethrin 5 Italy’s supreme court on Tuesday began hearing SilvioBerlusconi’s last appeal against a jail sentence and ban frompublic office in a case which could endanger the country’s shakycoalition government if the conviction is confirmed.
August 27th, 2020 at 6:09 pm
We’ll need to take up references buy retin a tretinoin gel Efforts to reach peaceful diplomatic solutions, whether it’s been with Palestinians, Syria, Iran, etc., ALWAYS angers Israel. The historically unsubstantiated “existential card” was played by Israel way too many times. It’s time for Israel to play the ‘peace card’ for change since the American Taxpayers refuse to continuously suffer due to proxy political as well as military conflicts in order NOT to “anger Israel”, and/thus, satisfy the World Zionists’ geopolitical agendas.
August 27th, 2020 at 6:09 pm
What company are you calling from? ventolin nebules 2.5mg salbutamol Pippa Middleton admirers have a new reason to cheer ‘Pip, Pip, hooray!’ She’s single! The British beauty has split from longtime beau Alex Loudon, according to multiple reports. Though Middleton, 27, brought Loudon to sister Kate’s wedding April 29, the pair reportedly found her new life in the spotlight too much to handle. ‘Pippa has become very high-profile, and it’s put a strain on things,’ a source told The Sun. ‘They’re moving in different circles.’ Indeed, Middleton and 30-year-old Loudon, a cricket player-turned-businessman, haven’t been seen together for several weeks.
August 27th, 2020 at 6:10 pm
Where did you go to university? how much is abilify without insurance Moreover, our adversaries will surely also use countermeasures during the attack, rendering the system ineffective. The enemy may also choose to launch a simultaneous salvo attack with several live warheads distributed among many decoys. The time of attack could also be planned such that the sun is located in an unfavorable location in the sky, possibly blinding or confusing the defensive sensors. For the sea-based âAegisâ missile defense system, another complication is if the enemy chooses to attack during rough weather when interceptors cannot safely be launched from the ships. None of these complicating factors are incorporated in the MDA’s demonstrations.
August 27th, 2020 at 6:11 pm
Whereabouts in are you from? citalopram and trazodone “Normally you prefer for them to start later on,” Snyder said Monday on the Big 12 coaches teleconference
August 27th, 2020 at 6:11 pm
Canada>Canada deer antler spray gnc canada Forest, which has a market capitalization of nearly $12 billion, is a New York-based drugmaker whose top products are treatments for depression and Alzheimer’s disease. The company also sells cardiovascular, respiratory and pain drugs.
August 27th, 2020 at 6:13 pm
What’s your number? ofloxacin ophthalmic solution for ears dosage Trading volume has been low as earnings season winds downand economic indicators present a mixed view of growth,complicating predictions of the Fed’s next policy action. TheFed has been buying $85 billion in bonds on each month to holdinterest rates lower. Some expect the Fed to taper bondpurchases as early as September if data shows the economy isimproving.
August 27th, 2020 at 6:15 pm
Will I be paid weekly or monthly? metformin order online canada
The auction was the first under a three-year-old legalframework that expands state control over Brazil’s most prolificoil region, the subsalt reserves off the coast of Rio that holdbillions of barrels of oil under a thick layer of salt beneaththe ocean floor. Under the new law, Petrobras must leaddevelopment of the fields as operator.
August 27th, 2020 at 6:15 pm
How many would you like? crestor reviews side effects There are 340,679 Nepalis in Qatar, according to figuresdistributed at the news conference, attributed to the NepaliEmbassy. Most of them work in construction in the wealthycountry that is preparing to host the 2022 soccer World Cup.
August 27th, 2020 at 6:15 pm
Yes, I love it! amlodipine tablet 5 mg
Tartabull’s older son Zach was a California high school football star and is now a male model, according to various reports. His younger son Quentin will graduate from a California high school next year, and has verbally committed to University of California as a defensive back, according to California.scout.com.
August 27th, 2020 at 6:16 pm
I like watching TV reviews for maxalt All four are due to make their first court appearance together Aug. 26 in Salt Lake City. Each has been released on $50,000 bond. Nakamura said some or all of the teens had attorneys, but he didn’t know the lawyers’ names.
August 27th, 2020 at 6:17 pm
Have you read any good books lately? penegra 100mg Bernstein analyst Pierre Ferragu said he doubted financial sponsors would be comfortable with $3 billion of debt, given the only collateral BlackBerry could offer is its patent portfolio, which he valued between $800 million and $1.5 billion.
August 27th, 2020 at 6:18 pm
How many are there in a book? tricor tab 145mg In fact this shape is actually flattering for curves and holds in any lumps or bumps, which is ideal to beat your post baby belly. Try a bold colour like Imogen and let the dress do the talking by wearing minimal jewellery and accessories.
August 27th, 2020 at 6:19 pm
This is the job description how much imodium ad to get high
RBS said on Friday it had picked the consortium led by U.S.private equity firm Corsair, which bid 600 million pounds ($960million) to take “a significant minority stake” of up to 49percent in the new bank when it lists on the stock market.
August 27th, 2020 at 6:19 pm
Where are you from? loratadine vs desloratadine difference After he offered the suggestion to Jobs, since they both had the same rare blood type, Jobs told Cook, “I’ll never let you do that
August 27th, 2020 at 6:20 pm
I’ll call back later what is sumatriptan used for Obama and his aides have been trying to navigate a tricky path on Egypt, expressing displeasure with the army’s actions while not entirely breaking a relationship crucial to U.S. security interests in the Middle East.
August 27th, 2020 at 6:22 pm
We’ll need to take up references motilium tablet fiyati Waiting outside the school for Diane, Kate calls Meg to complain about Dianeâs accusations. She instantly calls her stepson a horn dog, not realizing itâs actually Bert on the other end. Kate then sees Hillary and her friends. Upon walking up to them, she realizes that Hillary has used the vodka in a water bottle idea. Hillary begs Kate not to tell Diane. So, to keep Hillary out of trouble, Kate downs an entire water bottle of vodka. Obviously unable to drive, Kate lies to Diane about not being able to find her car keys. Thus, Kate ends up drunk in Dianeâs backseat.
August 27th, 2020 at 6:22 pm
Special Delivery micardis 40 mg price “You have to love yourself. That’s the single most powerful thing. Out of that springs: How are you eating? How are you exercising? How are you resting?” Peeples said. “I had to make a conscious effort to … begin loving myself wholly again, and that meant taking time in the morning to meditate.”
August 27th, 2020 at 6:23 pm
Looking for a job adcirca approval date The international police body has issued a wanted persons alert or “Red Notice” at Kenya’s request for British woman, Samantha Lewthwaite. Known as the “white widow” by some media, she’s wanted on charges of possession of explosives and conspiracy to commit a felony in 2011, according to Kenya’s Criminal Investigation Department, and not last weekend’s attack.
August 27th, 2020 at 6:23 pm
I’m interested in can i buy synthroid at gnc Central bank statistics from 2011 showed nine in 10 workingSaudis were employed by the public sector, which is largelyfunded by oil revenue. The IMF said reducing reliance on public-sector jobs must be a priority, which means Saudi nationals mustbecome more competitive and improve their skills.
August 27th, 2020 at 6:24 pm
I wanted to live abroad review ciprofloxacin A likely sticking point in negotiations will be whether LTSLohmann can succeed in preventing generic drugmakers fromlaunching cheap copies of its Exelon patch for mild to moderatedementia. Novartis has sued Actavis for trying to bringits version to market.
August 27th, 2020 at 6:24 pm
Insufficient funds when to wean off motilium “Unfortunately, it appears that Pastor Saeed was not among those reportedly released,” Jay Sekulow, ACLJ’s executive director, said Sept. 23. “We can confirm that Pastor Saeed’s family in Tehran saw him today during regular visitation hours, and as of noon Tehran time, he was still imprisoned and the family has not been notified that his status has changed.”
August 27th, 2020 at 6:26 pm
Can you hear me OK? forzest 20 review Weinberg added that signs of restocking in China should havelifted copper from its current doldrums. Data on Monday showedthat copper imports from China, the world’s top copper consumer,jumped 18 percent in September, reversing from a fall in August,as importers boosted orders ahead of a seasonal pickup.
August 27th, 2020 at 6:26 pm
Thanks for calling male enhancement pill uk âPlease, we gotta stop the killing, we have to stop, we have to stop!â Juannake Kenney said Saturday during a press conference, one day after her 6-year-old daughter was shot and seriously injured.
August 27th, 2020 at 6:27 pm
I quite like cooking lasix diuretic type “A number of the questions relate to areas which would be subject to negotiation should the people of Scotland vote to leave the UK for good. There is no doubt independence would mean a huge number of complex and irreversible changes to life in Scotland.”
August 27th, 2020 at 6:28 pm
It’s funny goodluck serevent package insert The evidence presented in Ramos’ decision demonstrates that Abbott’s claims are laughably false
August 27th, 2020 at 6:29 pm
I work for a publishers crestor off market No distinction was made between the two different forms of diabetes type 1 and type 2, which is much more common. However, the majority of studies involved older people over the age of 65, who are most likely to have type 2.
August 27th, 2020 at 6:30 pm
Can you hear me OK? purchase caduet ALBANY - Democratic mayoral front-runner Bill de Blasio will join Attorney General Eric Schneiderman’s bid to force smart phone manufacturers to protect customers from thieves who steal phones, scrub them clean and sell them on the black market.
August 27th, 2020 at 6:30 pm
Children with disabilities toprol xl 100mg bid It’s a pity that we Americans, Indians, Europeans apply the same yardstick of fairness, justice, equality, compassion and even feelings of horror to these radicals who live NOT in the present, but in the non-existent future (with Allah).
August 27th, 2020 at 6:31 pm
How much notice do you have to give? xenical sample menus Indeed, in what looks more and more like a concerted effort, policymakers are urging investors to reconsider the market’s conclusion that the Fed is about to pull the rug out from under the slow economic recovery. They seem to want investors to take a longer view of the policy change that’s fast approaching instead of focusing – as traders tend to do – on the imminent plan to reduce accommodation in the months ahead.
August 27th, 2020 at 6:32 pm
I’d like to pay this in, please how to wean off protonix Injury-hit Irish have signed Dragons lock Ian Nimmo on loan as cover. Captain Declan Danaher plays back row as Chris Hala’ufia has a knee problem. Exeter move Tom Johnson to No 8 and start Ben White at blindside.
August 27th, 2020 at 6:32 pm
I’ve just started at combivir precio chile
Ritchie Valens, 17 (1941-1959) and the Big Bopper, 28 (1930-1959):The fatal plane crash occurred on Feb. 3rd, 1959, which would become known as the ‘Day the Music Died.’ On its 50th anniversary, David Hinckley considered their place in the pantheon of rock n’ roll.
August 27th, 2020 at 6:32 pm
What are the hours of work? buy deer antler spray canada “What happened was they just put in their people in Al-Ahram and other state institutions, and nobody tried to reform the institutions themselves,” Hamamou said. “The saying goes if you are confused about who is ruling Egypt, just look at the headlines of Al-Ahram.”
August 27th, 2020 at 6:34 pm
I’d like to tell you about a change of address lidocaine cream boots uk
“We need to think about the dynamics within relationships that may result in someone both perpetrating and being victimized by their partner; as well as the extent to which dating abuse may follow a teen from one relationship to another,” Ybarra said.
August 27th, 2020 at 6:34 pm
Thanks for calling combien de temps avant de prendre le viagra The Telegraph led an eight-month Hands Off Our Land campaign last year before the National Planning Policy Framework (NPPF) was set, urging the Government not to weaken protections for greenfield and green belt land.
August 27th, 2020 at 6:36 pm
Will I get paid for overtime? para que sirve el medicamento ciprofloxacino 500 mg Earlier on Thursday, Chambriard said that at least 12companies had paid the initial entry fee. The ANP will publish acomplete list of preliminary participants on Thursday, theregulator’s press office said on Wednesday.
August 27th, 2020 at 6:36 pm
Do you know what extension he’s on? how much does ventolin cost in australia As a vegetable, Florence fennel is more than versatile: braise or steam it then serve with fish or pork; deep fry it in light tempura batter; try it sliced with a mandolin with shaved Parmesan, or chopped as a crudité to dip in hummus. My favourite dish is fennel bulbs caramelised in butter and sugar, then covered with goats’ cheese, scattered with roast fennel seeds and grilled. Fennel loses its flavour soon after it has been cut. Revive it, packed in ice with a brief sojourn in the fridge.
August 27th, 2020 at 6:37 pm
Hold the line, please how quickly does bactrim cause relief Stanfield urged anyone with measles symptoms to call their doctor before seeking medical attention to avoid exposing others to the highly contagious illness.
August 27th, 2020 at 6:38 pm
I’d like to take the job sinequan canada
She said the agent refused to say why he’d stopped her. Two other agents approached the car. One pulled out a retractable knife, threatened to cut her out of her seat belt if she didn’t get out of the car and took the keys from her ignition.
August 27th, 2020 at 6:38 pm
I enjoy travelling viagra for sale using paypal Keith Mallinson, a longtime telecom industry analyst, saidthat while the concepts and technologies Zuckerberg cites couldbe viable, the commercial interests of big companies andgovernment politics could create bigger obstacles.
August 27th, 2020 at 6:38 pm
What do you do? micardis plus price uk The 22-month contract, which runs through May 2015, marks asignificant win for Raytheon, said Loren Thompson, chiefoperating officer of the Virginia-based Lexington Institute,noting that there were few if any other significant electronicwarfare contracts expected in coming years.
August 27th, 2020 at 6:39 pm
I’ve been made redundant how does lamisil work We committed ourselves to peaceful protesting, even if this means sacrificing ourselves with our bare chests. We will never admit to the allegations that our supporters possess weapons or that they are adopting a non-peaceful path.Â
August 27th, 2020 at 6:40 pm
How many days will it take for the cheque to clear? 75 mg of effexor enough Bikes aren’t like cars for several reasons. They fall over if you forget to put your feet down, they accelerate like the billowing forces of hell are on your tail, and they are much easier to put to one side and forget.
August 27th, 2020 at 6:40 pm
I’d like to send this parcel to clarithromycin 500 mg
Fund manager Don Taylor of the Franklin Rising Dividends Fund says the most “bond-like” investments lost the most value and have been slowest to recover amid concerns that the Federal Reserve might let yields rise soon on signs that the economy is strengthening.
August 27th, 2020 at 6:42 pm
I’m a trainee enalapril 10mg tablets His widow Marina, who has also called for a public inquiry, said the rejection was a “political decision”, adding: “Were they trying to protect the Russian state? Were they trying to protect national security secrets?”
August 27th, 2020 at 6:42 pm
A few months xength x1 in canada The astutely engineered suspension responds efficiently to the vehicle’s different drive modes. Also, of note, the new Stingray has technology that monitors the temperature of the specially made Michelin tires and adjusts the stability and traction control systems to take advantage of warm rubber’s extra grip. Chevy says this is a unique new technology that carries over from racing.
August 27th, 2020 at 6:43 pm
I need to charge up my phone risperdal 1 mg yan etkileri “When you have to sit down and explain to a 5-year-old why he can’t go to school, it’s a difficult conversation,” Virginia resident Brian Katz, whose two children attend the Smithsonian Early Enrichment Center housed in the Natural History Museum, told a local Fox television station.
August 27th, 2020 at 6:45 pm
Could you tell me the number for ? overnight seroquel Over the weekend, the central al-Fateh mosque became the new battleground for unrest as pro-Morsi protesters marched to Ramses Square in a self-declared “Friday of Anger.” After fighting broke out with security forces, leaving 173 dead on Friday, protesters used the mosque as a makeshift hospital and morgue before it was surrounded, then cleared, by security forces Saturday.
August 27th, 2020 at 6:46 pm
Why did you come to ? medrol dose pack online Archaeologists from the University of Southampton have revealed for the first time the plan of a network of buildings in a once thriving medieval city at the historic site of Old Sarum, near Salisbury.
August 27th, 2020 at 6:46 pm
I can’t get through at the moment albendazole prices âWe really think that a Wi-Fi only tablet is good, but it is not good enough,â said AT&T senior VP Chris Penrose, speaking at the event. The cost of adding a cellular module to tablets is also going down, Penrose said.
August 27th, 2020 at 6:46 pm
Very funny pictures where can i buy stromectol ivermectin The No. 2 U.S. burger chain also raised its quarterlydividend by a penny, to 5 cents a share, and said it would sellabout 425 company-operated restaurants by mid-2014 as part of adrive to improve its finances.
August 27th, 2020 at 6:46 pm
How long are you planning to stay here? cheapest place to buy accutane online “Couldn’t have picked a more beautiful & perfect song to start the year with,” she tweeted, about her session. “Thank you [Alex Anders] & [Adam Anders] for a great recording session today⦠You guys are the best.”
August 27th, 2020 at 6:47 pm
I’m a partner in take clomid at night or in morning “When we speak of resignation, that is an easy personal decision to make but would be irresponsible for the country… I have heard no convincing arguments explaining how resignation would automatically solve the problems of the country.”
August 27th, 2020 at 6:48 pm
The United States rogaine foam price in pakistan Bae has acknowledged being a missionary and has said he conducted religious services in the North, which is hostile to outsiders advocating religious causes within its tightly controlled political system.
August 27th, 2020 at 6:49 pm
What’s the interest rate on this account? lithium eskalith classification Brailsford laughed: “Tim told him, ‘there’s two bulls, one old bull and one young really young bull on top of a hill, looking down on a paddock of cows. And the young bull turns to the old bull and says ‘let’s run down and —- a cow!’ And the old bull says ‘tell you what son, let’s walk down and —- ’em all’. Basically that was our motto for the day!”
August 27th, 2020 at 6:50 pm
It’s funny goodluck polo store artane Itâs an elbow here and there, a penalty here and there, a bad bounce here and there, the kind of things that were more there than here in the old days. Problem is, theyâre adding up faster than any Ws. A lot of stuff to think about.
August 27th, 2020 at 6:51 pm
Withdraw cash community pharmacy services gretna nebraska
Perhaps Morgan Stanley, which held a global minute’s silence on September 11 and has raised millions for the victims of 9/11, might save a different date next year. A spokesman for Morgan Stanley declined to comment.
August 27th, 2020 at 6:52 pm
I’m in my first year at university vpxl uk Today, almost 300 syndicates are on AngelList, includingthose created by Mayer, Hoffman and Twitter co-founders BizStone and Evan Williams. Digg co-founder Kevin Rose has alreadyraised commitments of $1.4 million for his, with social-networkPath founder Dave Morin second at $963,000.
August 27th, 2020 at 6:54 pm
I don’t like pubs methotrexate tablets ip 10mg “If it looks like a private ducal estate set up to provide an heir to the throne and it quacks like a private ducal estate set up to provide an heir to the throne, can one assume that it might just possibly be a private ducal estate set up to provide an heir to the throne?”, Richard Bacon asked.
August 27th, 2020 at 6:54 pm
How much will it cost to send this letter to ? generic lexapro online no prescription Sumwalt, who spoke at a media briefing near the crash site,had said on Friday that the pilots received a low altitudewarning barely seven seconds before the sound of impact. Herepeated that in his remarks on Saturday but did not say whetherthe alert had triggered any attempt by the crew members todisengage the autopilot as part of a last-ditch attempt to abortlanding and re-gain altitude.
August 27th, 2020 at 6:54 pm
I was made redundant two months ago aldactone costo While Bullard and other more dovish policymakers want to keep buying assets until inflation rises and unemployment drops, Plosser and the more hawkish of the Fed’s 19 policymakers want to reduce the pace sooner than later.
August 27th, 2020 at 6:54 pm
I’m on a course at the moment pariet vs zantac Specifically, the researchers suggest using fences to exclude the unwanted, earthbound customers, and dishing up the extra meat for the vultures in random locations instead of re-stocking a regular carrion pantry.
August 27th, 2020 at 6:55 pm
How much will it cost to send this letter to ? buy betnovate c cream uk Deloitte & Touche LLP faces a fine of up to 20million pounds and the suspension of one of its partners after atribunal ruled the accountants had shown a “deliberatedisregard” for professional ethics in its handling of the saleof defunct carmaker MG Rover Group.
August 27th, 2020 at 6:55 pm
A jiffy bag reputable suppliers of generic viagra Proportions wise itâs very neat and tidy, as well as being nicely balanced, nicely skinny and Samsung is prepping a wide range of interchangeable coloured back panels, covers and accessories for you to go nuts with. Thereâs even one with a window.
August 27th, 2020 at 6:55 pm
Very Good Site long hair rogaine In November 2012, the SEC dropped civil charges againstEdward Steffelin, a former managing director at GSC CapitalCorp, in light of what a spokesman said was “information thatcame to light as the litigation progressed.”
August 27th, 2020 at 6:56 pm
Is there ? cost of nexium in usa “The air disaster highlights serious public concern of whether pilots are overly dependent on technology and are not retaining the skills required to properly fly complex commercial aircraft.”
August 27th, 2020 at 6:58 pm
Directory enquiries cheapest place to buy alli uk “Air Canada has been providing the best available information to media on this matter. However, these comments do not refer to the search for Larry by Air Canada employees that is ongoing or our interest in returning him safely,” it said.
August 27th, 2020 at 6:59 pm
What line of work are you in? prozac zoloft equivalent dose I overheard two telling comments at the screening. A woman in her mid-to-late twenties sitting next to me leaned over to her friend during a scene in which the story’s love triangle emerges, and said, “This isn’t really believable.” Of course, this was after learning the movie’s central premise and witnessing numerous demons being slaughtered and improbable, gravity-defying events. Then on the way out of the theater, that same woman said to her friend, “That was really good!”
August 27th, 2020 at 7:00 pm
I’m sorry, he’s order montelukast online Bill Ayers, who helped lead the Weather Underground as it waged a bloody war against the U.S. government in the 1960s, then went on to a career in academia, recently urged those attending his book promotion to be “good citizens” and “moral people.”
August 27th, 2020 at 7:02 pm
I’d like to apply for this job m drive transmission with engine brake The most recent release also includes more integration with third-party apps and hardware devices, such as MyFitnessPal and FitBit. When asked “What’s next?” for Runkeeper, Jacobs said he would like to see the app get smarter.
August 27th, 2020 at 7:02 pm
We need someone with qualifications glucophage xr 500 price Mr Taylor maintained that his fellow FPC members on the committee, which is chaired by Bank Governor Mark Carney, “have our eye on developments”. However, he also voiced concerns that the expectations placed upon the FPC “are expanding so fast”.
August 27th, 2020 at 7:02 pm
I’ve got a very weak signal kruidvat ibuprofen âItâs odd because youâre used to presenting the truth [as a journalist],â says Watt, âbut in order for us to present the truth and to show how our brains really work, we have to deceive people to begin with.â
August 27th, 2020 at 7:02 pm
I’d like , please vigora 100 how it works Amazon announced Monday that it would add 7,000 new U.S. jobs nationwide, including 2,000 customer service positions and 5,000 full-time fulfillment employees – warehouse workers who help ship goods to consumers.
August 27th, 2020 at 7:02 pm
Can I use your phone? children’s motrin dose by weight As a non-Scottish baker, this sets one up for a storm, so I am not attempting authentic shortbread this week but an interesting, summery version made with semolina, flavoured with fresh lemon zest. These are lovely biscuits to have with ice cream, or to wrap in paper and take on a picnic. The lemon thyme is optional, but makes a grown-up dinner party biscuit to eat with panna cotta or fresh fromage blanc served with honey.
August 27th, 2020 at 7:03 pm
Canada>Canada sominex original formula dosage WASHINGTON, Nov 20 (Reuters) - An explosion at oil and gasoperator Fieldwood Energy’s Echo Platform in the Gulf of Mexicoon Thursday killed one person and injured at least one, but nopollution was reported, a U.S
August 27th, 2020 at 7:03 pm
A pension scheme fake zenegra Now he wants you to believe that he ended the season hurt because the Yankees were trying to make the playoffs and he just had to keep dragging his bad legs out there. As if somehow he was the victim of the Yankees grinding away trying to get the second wild card in the American League.
August 27th, 2020 at 7:03 pm
I came here to work lopressor cost price Tayyeb-Nia is an economist who has specialised in the studyof inflation, which Rouhani said last month stood at 42 percentand which must be reduced to bring a measure of economic reliefto Irananians.
August 27th, 2020 at 7:05 pm
I’d like to pay this cheque in, please can you buy amoxicillin over the counter in australia Jason W. Kreiss, an attorney representing the family, said Hernandez-Llach would likely not have been prosecuted over the spray-painting and would have probably faced a punishment of community service.
August 27th, 2020 at 7:06 pm
Will I be paid weekly or monthly? hoodia rite aid
“There are clauses in the agreement which allow Chevron toturn hundreds of kilometres of Ukraine into swamp and desert.Chevron would have the right to use sand, stone, undergroundwater supplies and other water sources on the basis ofagreements in and beyond the (agreed) area.
August 27th, 2020 at 7:08 pm
Very interesting tale prozac ve desyrel kullananlar Meanwhile Scottish Secretary Michael Moore said the pandas project marked “another significant chapter in the relationship between China and the UK”, and Deputy Prime Minister Nick Clegg said it reflected the strength of Britain’s relationship with the Asian powerhouse.
August 27th, 2020 at 7:08 pm
magic story very thanks buy lipitor online cheap David Mason is the entrepreneur behind Anthony Sinclair, the bespoke tailor which dressed James Bond. Many of Sean Connery’s suits for the role of 007 were made by the business, including the three-piece suit from Goldfinger.
August 27th, 2020 at 7:10 pm
I’d like to pay this in, please farmacia online levitra generico A report showed that, in dollar terms, headline U.S. durablegoods orders totalled a record $244.5 billion, finallysurpassing the previous peak of $242.96 billion seen in December2007, the month the United States entered recession.
August 27th, 2020 at 7:10 pm
I’d like to apply for this job silvitra cheap
Reyna contracted the brain-eating amoeba called Naegleria fowleri on Aug. 3 while knee boarding in a ditch with his friends near his house in LaBelle. Naegleria fowleri is found in warm, fresh water, and the amoeba enters the body through the nose and travels to the brain.
August 27th, 2020 at 7:10 pm
Is it convenient to talk at the moment? crestor tabletas de 5mg Pena Nieto said he hoped the initiative would be debated by Congress during a special legislative period set to begin in mid-August, setting up what is likely to be a heated debate over the future of Mexico’s oil riches.
August 27th, 2020 at 7:11 pm
Stolen credit card price cytotec quiapo He said that the candles were fakes, adding: “I’d say more ‘asked to leave’ than ‘kicked out’. Either way, they didn’t appreciate it some of the staff found it funny, but others clearly did not.”
August 27th, 2020 at 7:11 pm
Do you have any exams coming up? retail cost for crestor Uruguay’s key match could be on Oct 11, when they travel to fourth-placed Ecuador, whose campaign is on the slide after a bright start. Ecuador will hope the high altitude of Quito makes the difference.
August 27th, 2020 at 7:11 pm
I never went to university kamagra gel sachets uk A co-op apartment on the primo portion of Central Park West just went on the market for $748,000 â practically one-tenth of the average price for a home on the strip below the American Museum of Natural History.
August 27th, 2020 at 7:12 pm
I’m at Liverpool University clomipramine hydrochloride overdose Chicago-based Boeing and European rival Airbus have prospered as airlines around the world have gone on a shopping spree, helped by rising demand for travel and cheap financing
August 27th, 2020 at 7:12 pm
I can’t get through at the moment discount levitra online
The tracks were discovered by a team from the university’s Museum of the North in Fairbanks after a 500-mile boat trip, the university said last week. Earth Sciences Curator Pat Druckenmiller said the tracks were left by a diverse group of dinosaurs, both carnivores and herbivores.
August 27th, 2020 at 7:14 pm
I’ve only just arrived isotretinoin medication guide Sources said South Korean officials were ordered to keep mum in order to prevent media scrutiny from swaying the discussions, after public pressure was seen to have played a part in Seoul’s rejection in September of Boeing’s bid to supply 60 warplanes.
August 27th, 2020 at 7:15 pm
I’ll send you a text viagra jelly review Santos declined to provide further details of thelegislation, such as which types of data would be covered by thelaw or which categories of companies would be subject to suchrules, saying such questions were still under study.
August 27th, 2020 at 7:16 pm
I love this site acyclovir ointment 5 Now Iagnemma and researchers from Washington University in St. Louis and the Jet Propulsion Laboratory (JPL) in Pasadena, Calif., have developed a model called Artemis that accurately simulates rover mobility over various types of soil and terrain.
August 27th, 2020 at 7:18 pm
Whereabouts in are you from? where to buy viagra over the counter australia U.S. diplomat Valerie Ullrich said Saudi authoritiescontinued to detain people without due process insecurity-related cases. “We are very concerned that Saudicitizens have been harassed, targeted, detained, and punishedfor simply expressing their beliefs, opinions, and views,” shesaid.
August 27th, 2020 at 7:18 pm
What do you do? generic xenical 120 mg The Miss America organization doles out over $45 million in cash and tuition scholarship assistance to the 12,000 some women competing every year, making the pageant an attractive option for those paying for college. For some Miss Alaska contestants, and contestants in other states, competing in the pageant means turning dreams of being able to afford college into a reality.
August 27th, 2020 at 7:18 pm
Could I ask who’s calling? glucophage xr canada pharmacy Police are investigating the cause of blast. Safety inspections will be conducted across the city of Guilin, in a search for illegal explosives, said a city government statement. Guilin, a popular tourist city in Guangxi, is famous for its karst scenery.
August 27th, 2020 at 7:19 pm
very best job cheapest viagra anywhere When Sally told Phil she had in fact drunkenly implied to this couple that the trip was open to all comers, she agreed to rectify the situation. Which she did, even though it caused her huge strain with her friends. But as she admitted when they came back from the trip: “my relationship with Phil is far more important to me than any of my friends”.
August 27th, 2020 at 7:19 pm
A staff restaurant clomiphene citrate 50 mg cost It’s been a big year for pop star makeup collaborations. MAC has collaborated with Rihanna on a series of capsule make-up collections, although it hasn’t just been about the girls. One Direction also released their own line of makeup, called Little Things, with UK brand MUA.
August 27th, 2020 at 7:19 pm
I’ve come to collect a parcel viagra uten resept spania Some European countries have also started telling banks tohold more capital than the minimum levels. In Britain,regulators warned Barclays they would not accept anyplans to restrict lending after telling it to ramp up itsleverage ratio to 3 percent, from 2.5 percent now.
August 27th, 2020 at 7:19 pm
Punk not dead dbol vs anavar for strength “We have, on the one hand, the bankers and the lobbyists and the politicians that have been bought by those lobbyists and think that any regulation is too much regulation,” said Cathy O’Neil, a former quantitative hedge-fund analyst who is the organizer of the Occupy Wall Street alternative-bank group, which wants to make the financial system more accountable and transparent.
August 27th, 2020 at 7:21 pm
I don’t know what I want to do after university prijs van ventolin “The results of the RCSI malaria vaccine trial, which demonstrate both safety for the patient and a positive clinical and immunological response, are very promising and represent an important step in the development of an effective vaccine for the disease,” commented the study’s senior author, Prof Sam McConkey, head of the RCSI’s Department of International Health and Tropical Medicine.
August 27th, 2020 at 7:22 pm
A few months harga salep triamcinolone acetonide Acting Assistant Chief Constable Ken McIntosh, of North Yorkshire Police said: âI encourage our rural communities to buy into Operation Hawk because with their support and local knowledge they can help make this initiative a success.â
August 27th, 2020 at 7:22 pm
A company car alli cheap Sortedfood was a concept that began a few years back around a pub table: as a group of school mates sat round their pints, it was clear that the student diet fuelling their time at uni was nowhere near what it could or should be. That was all about to change.
August 27th, 2020 at 7:25 pm
I like it a lot cost comparison viagra vs cialis 250 More than 150 law enforcement officers on foot and on horseback had descended on the central Idaho wilderness in search of James Lee DiMaggio, 40, after a group of backcountry horsemen told police that they had spotted the pair on Wednesday.
August 27th, 2020 at 7:25 pm
I’m interested in this position satibo apoteka
A top Treasury official said on Thursday the government wasconsidering changes that could force shareholders buying lessthan 30 percent of a company to launch a takeover bid when thecompany changes hands.
August 27th, 2020 at 7:26 pm
What sort of music do you like? lisinopril dosage 40 mg But bosses shouldnât rush to glue workers to their chairs just yet. The research is only a first stab at teasing out how a sociable lunch affects work performance, says study leader Werner Sommer of Humboldt University in Berlin.
August 27th, 2020 at 7:26 pm
It’s OK blokium 50 mg atenolol One City seer foresaw that the “happy event” will create a “feel-good factor”, and that – hold the front page – support to the economy will come from sales of souvenirs and commemorative items.
August 27th, 2020 at 7:26 pm
Very funny pictures adcirca tadalafil drug His low-price, high-volume approach helped secure regular government contracts, and he often sold cars to the state. In 1954, Lambrecht drove then-Gov. Robert Crosby down Main Street in a parade celebrating the 100-year anniversary of Nebraska as a territory.
August 27th, 2020 at 7:27 pm
I’m training to be an engineer buy xenical or orlistat âThe FBI had info that two to three members of his Knicks were shaving for a coke dealer,â Touhy told The News. âAnd that informants believed that the players were betting on the games themselves â betting on the Knicks to lose.â
August 27th, 2020 at 7:27 pm
The National Gallery lipitor price comparison But members of Congress will also be able to purchase their insurance under terms that are more favorable than other employees â in government or in business â who have access to employer-provided health care.
August 27th, 2020 at 7:28 pm
magic story very thanks cheap kamagra uk viagra Perhaps more importantly, Now TV is one of the only ways to watch certain live sports coverage without opting for a full Sky subscription. For customers where installing a satellite dish isn’t an option, this could be a major bonus to buying an LG TV in the near future.
August 27th, 2020 at 7:30 pm
How long have you lived here? vimax lot 1212 Jim Jordan, R-Ohio, one of the most conservative members of Congress and a leader of the House’s ultra-right Freedom Caucus.
August 27th, 2020 at 7:30 pm
Have you got a current driving licence? buy famvir tablets âThe baseball bat is the ubiquitous blunt instrument,â says Jef Klein, author of âThe History and Stories of the Best Bars of New Yorkâ and a bartender for 14 years who found a bat at every pub that hired her. âItâs like the lowest of the low-tech weapons. Itâs the handgun of the Stone Age. And it really works.â
August 27th, 2020 at 7:32 pm
We’re at university together costco valtrex generic
Now it looks likely that the thirty-eight-year-old third baseman will be near 40 by the time he is allowed back on the field. The Yankees still owe him about $100 million on a contract that doesnât expire for four and a half more seasons.
August 27th, 2020 at 7:34 pm
Do you know each other? what mg topamax lose weight the only way to protect ourselves from the abomination which has become the livestock drugging industry is to eat purely organic and drug-free meat products. make a statement with your purchasing habits and tell Merck, Eli Lilly and the other drug pushers and the meat producers that feed pharmaceuticals to their cattle that you will not consume their tainted and contaminated meats by purchasing locally sourced/organic meats only.
August 27th, 2020 at 7:34 pm
Sorry, you must have the wrong number buy sleepwell duet mattress online india
We have no better drugs than opioids for controlling most kinds of severe pain, but these drugs are also dangerous. There just is no way around it until we invent a non-addictive, non-euphoric opioid-level analgesic that doesn’t cause respiratory depression. We have to use the agents we have, and carefully!
August 27th, 2020 at 7:34 pm
I’d like to cancel a cheque how long should i be off coumadin before surgery Nothing substantive to add, it’s just nice to see someone who can look at something that clearly means a lot to them and view it and criticism of it/Creator objectively without releasing a Kraken of defensiveness. There was a great article on EG regarding the killer as victim that made me profoundly certain that I would be throwing the book against a wall, much as I’ve done with other of Card’s books (before I knew anything about him as a person.)
August 27th, 2020 at 7:35 pm
I’ve got a part-time job viagra generic cheap
“The Chancellor expressed her concern to Putin over thearrest of the crew of the Greenpeace boat, impounded in Russia,and voiced her hope that this case will soon be resolved,”Merkel’s spokesman said in a statement.
August 27th, 2020 at 7:35 pm
I’m sorry, she’s where can i get bimatoprost cheap “I have a very clear message for Google, Bing, Yahoo and therest. You have a duty to act on this - and it is a moral duty,”Cameron was due to say in a speech on Monday, according to anadvance text, demanding that the companies report back to him inOctober on their progress.
August 27th, 2020 at 7:35 pm
Would you like to leave a message? penegra express dosage
Ubisoft’s historical action-game “Assassin’s Creed IV: Black Flag” came in third place in the poll with 19 percent expressing interest. Electronic Arts’ “Madden NFL 25″ and shooter “Battlefield 4″ were the participants’ fourth and fifth choices, respectively.
August 27th, 2020 at 7:35 pm
The United States esomeprazole 40 mg in patients Similar protests broke out in June last year after thegovernment reduced fuel subsidies as part of a plan to containits ballooning deficit, but they ended in the face of a securitycrackdown and Sudan’s intense summer heat.
August 27th, 2020 at 7:39 pm
I’ve been made redundant what does 150 mg trazodone do The sprawling Asian conglomerate Swire, the largestshareholder in airline Cathay Pacific and distributor of brandsRepetto, Chevignon and Columbia in Hong Kong and mainland China,is looking to team up with a private equity firm to make a bidfor Lancel, the sources added.
August 27th, 2020 at 7:39 pm
I’m interested in this position alavert rxlist “We are now for the first time showing that (those rates are) slowing down,” Ann Albright told Reuters Health
August 27th, 2020 at 7:42 pm
real beauty page celexa to lexapro
NEW YORK, Sept 26 (Reuters) - The S&P 500 and Dow snappedfive-day losing streaks on Thursday on positive job market databut gains were limited as investors worried if Washingtonlawmakers would pass bills to avoid a government shutdown andpossible U.S. debt default on time.
August 27th, 2020 at 7:42 pm
I’d like to pay this in, please cat costa cipralex Kate Middleton’s parents, Michael and Carole Middleton, were the first to visit their new grandson at the hospital in London where the royal baby was born Monday. They spent a little more than an hour at the hospital.
August 27th, 2020 at 7:42 pm
I was born in Australia but grew up in England buy albuterol sulfate syrup At the same time, evidence of an improving jobs picture, as well as dovish statements (now partly taken back) from the Fed have convinced markets that they are on a path towards ‘normal’ interest rates. In other words, higher rates.
August 27th, 2020 at 7:42 pm
What do you study? amlodipine 10 mg buy online The Asiana Airlines Boeing 777 was flying 25 percent slowerthan normal for a descent in the run-up to Saturday’s crash,according to U.S. National Transportation Safety BoardChairwoman Deborah Hersman.
August 27th, 2020 at 7:42 pm
On another call buy estradiol transdermal patch
âThe United States in 2014 will be the largest andstrongest growing part of our businessâ removing the U.K. fromits top spot as the companyâs largest market for the first time,Chief Executive Officer Andrew McNaughton said in a phoneinterview. âProfit, whilst down on where we were last year, isin line with what weâve been advising.â
August 27th, 2020 at 7:43 pm
I’d like to cancel this standing order cost for lipitor Some observers argue that a grand coalition, with a bigmajority in parliament, could push through economic policychanges far more easily than the outgoing government with theFDP, which has been criticised for its lack of reforms.
August 27th, 2020 at 7:43 pm
How much were you paid in your last job? priligy 60 mg posologia “I want to make sure everybody understands that we need to take these precautions,” he said. “If it’s something that looks suspicious, it’s our obligation to make sure it’s not something that can harm someone.
August 27th, 2020 at 7:43 pm
I’d like to speak to someone about a mortgage como usar la crema himcolin The scientists analyzed this core by running two electrodes along the ice to measure high electrical conductivity associated with each summer season. This allowed the researchers to identify the annual layers in the core. Evidence of greater warming turned up in layers associated with 18,000 to 22,000 years ago, the beginning of the last deglaciation.
August 27th, 2020 at 7:46 pm
Very Good Site paxil zoloft same National Transportation Safety Board investigator Patrick Murray said Saturday the plane was upside down when it struck a house at about a 60 degree angle. He said the pilot was making his first approach to the airport and did not declare an emergency before the crash.
August 27th, 2020 at 7:47 pm
In tens, please (ten pound notes) fertile xy uk
The Syrian Observatory for Human Rights, an anti-Assad monitoring group, cited activists on Friday in Khan al-Assal who said that more than 150 soldiers were killed on Monday and Tuesday in and around the town, including 51 soldiers and officers who were executed.
August 27th, 2020 at 7:49 pm
Good crew it’s cool tretinoin over the counter But as far as playing with him, I’m here now, but I would always love to play with Kobe.”
tretinoin over the counter But as far as playing with him, I’m here now, but I would always love to play with Kobe.”
August 27th, 2020 at 7:49 pm
magic story very thanks micardis online Calling itself a pit stop, the port operator backed byAsia’s richest man, Li Ka-shing, derives 70 percent of itsrevenues from transhipments where super-sized ships movecontainers carrying finished goods to smaller vessels fortransport to nearby markets.
August 27th, 2020 at 7:50 pm
I’d like to cancel this standing order where can i order nolvadex Schad becomes the first person executed in Arizona in 2013and Yowell would be the 14th to be executed in Texas. Overall, 28 people have been executed in the United States thisyear, according to the Death Penalty Information Center.
August 27th, 2020 at 7:50 pm
Could you send me an application form? nexium alternatives uk To make matters worse, an entirely new, secretive unilateralism is emerging, the consequence of an obsession with security and reorienting U.S. efforts in the war on terror from overt to covert operations. It has been mired heavily in surveillance and spying across both administrations. Between the two, a growing distrust and suspicion now colors international opinion of the U.S. and there is more resentment than at any time in recent memory.
August 27th, 2020 at 7:50 pm
perfect design thanks wellbutrin bupropion uk French peer GDF Suez has led the way in investingin power generation abroad, while Iberdrola has focused onforeign grids. Following takeovers of U.S. Energy East andScottish Power, it gets nearly half of its profit from networks.
August 27th, 2020 at 7:51 pm
Please wait 2.5 mg albuterol inhalation solution If you are interested in becoming a Dementia Friend or in helping create more dementia-friendly communities, go to dementiafriends.org.uk to find your nearest information session or to volunteer as a Dementia Friends Champion.
August 27th, 2020 at 7:51 pm
I want to make a withdrawal lansoprazole uk The juror’s statement adds to pleas from around the country to change the Stand Your Ground laws that more than 30 states have adopted. In Florida, demonstrators occupied a part of the governor’s office demanding that the state repeal or curtail its 2005 law.
August 27th, 2020 at 7:51 pm
Hold the line, please mirtazapine 15mg uk
New meaning and fresh insight are brought to the ancient text in an array of forms including essays, stories, poems, scripts, plays, a graphic novel and an architectural rendering. Contributors include Aimee Bender, Rich Cohen, A.J. Jacobs, Josh Radnor, Rick Meyerowitz and Daily News feature writer Justin Rocket Silverman. Remember, the first night of Chanukah comes early this year â Nov. 27.
August 27th, 2020 at 7:53 pm
I’ve been cut off cheap premarin cream Energy UK, the trade body representing the six largest energy firms, said it would “freeze the money to build and renew power stations, freeze the jobs and livelihoods of the 600,000-plus people dependent on the energy industry and make the prospect of energy shortages a reality, pushing up the prices for everyone.”
August 27th, 2020 at 7:55 pm
I’d like to order some foreign currency pristiq medicine side effects The diverging numbers, the report concluded, “are confusing for national and global accountability.” If the international community can’t agree on precise child health figures, stakeholders should at least, the authors pleaded, come to a conclusion on the broad progress toward internationally agreed upon goals.
August 27th, 2020 at 7:58 pm
Hello good day cost of wellbutrin with insurance The United Nations Security Council issued a statement Wednesday evening agreeing on the need for ‘clarity’ on the alleged gas attack; but the statement failed to call for a U.N. probe Reuters reported.
August 27th, 2020 at 7:58 pm
Which team do you support? procyclidine 5mg patient information leaflet “India will become the first Asian country to have achieved this and if it happens in the maiden attempt itself, India could become the first country in the world to have reached distant Mars on its own steam in the first attempt,” said Isro chairman K Radhakrishnan as it approached.
August 27th, 2020 at 7:59 pm
US dollars zenegra canada Medics have reported an increase in the number of cases involving PMA, similar to MDMA â the chemical in ecstasy â but which, according to drugs charity Frank, is more poisonous and can kill at lower doses.
August 27th, 2020 at 7:59 pm
Until August how to wean off zetia Bruce Bochy wasn’t willing to go with the small sampling size and make Yasiel Puig an All-Star, though he might have been tempted to change his mind after watching the rookie sensation do a little bit of everything in helping the Dodgers to a win Sunday in San Francisco.
August 27th, 2020 at 7:59 pm
Are you a student? can you get zyban in australia “I don’t care either way how I got this trophy â I got it,” Mickelson said. “And it just so happened to be with one of the best rounds of my career, which is really the way I’ve played my entire career. I’ve always tried to go out and get it. I don’t want anybody to hand it to me. I want to go out and get it. And today, I did.”
August 27th, 2020 at 7:59 pm
I work with computers buy cheap alli online uk “We will work very, very hard together with others, in order to bring parties together to find a peaceful resolution that grows the democracy and respects the rights of everybody,” Kerry said before a meeting United Arab Emirates Foreign Minister Sheikh Abdullah bin Zayed in London.
August 27th, 2020 at 7:59 pm
On another call methylprednisolone 4mg dosepak 21’s The celebrities arrived, cooed and quaffed, then they scarpered off to the next glitterati event, leaving BMW to look at its newly launched i3 electric car. With the A-, B- and C-listers now long gone to another party,â¦
August 27th, 2020 at 7:59 pm
I’d like to cancel a cheque safe purchase of viagra In addition, a small positive rate of inflation is likely to be better than a zero rate because it is more likely to be a credible goal. If the marginal cost of inflation around zero is perceived to be low and the short-run marginal benefit from some small inflation is positive, it would be very difficult to persuade people thatthe rate of inflation will remain at zero.
August 27th, 2020 at 8:00 pm
I’m doing a phd in chemistry pil yasmin murah Adjusted earnings before interest, taxes, depreciation andamortization, a gauge of operating profit known as EBITDA, fell 27 percent from a year earlier to 94 million reais, missing theaverage estimate of 98.4 million reais in a Reuters survey.
August 27th, 2020 at 8:03 pm
What are the hours of work? cost zithromax without insurance ESPN’s article on this same story makes LA Times handling of it look like a puff-piece. The NBA Rookie Transition Program is a program designed to teach NBA rookies about the frequent problems NBA players encounter with women and drugs:
August 27th, 2020 at 8:03 pm
Directory enquiries chloroquine phosphate coupon “Canada’s not serious about having foreign direct investmentand they are not serious about opening their telecom market,”Sawiris said. “It’s a waste of time, and investors like us wedon’t have time to pay lawyers and accounting firms and do duediligence and block our capital for six, eight months.”
August 27th, 2020 at 8:07 pm
Could I have a statement, please? methocarbamol robaxin high And should the unexpected aerial journey leave the first-time visitor a touch sweaty under the collar, there’s a ready-made outdoor shower unit at hand. It comes in the form of an old, see-through British Telecom phone box, in which the handset has been converted into a shower head. “It’s extremely simple,” explains our host enthusiastically. “The water tank sits on top of the phone box, and when you want to shower, you just take the phone off the hook and hold it over your head.
August 27th, 2020 at 8:07 pm
I can’t get through at the moment www.focusedhealthcare.co.uk For China, âits own national assessment and the level ofmounting public concern about air pollution are moreinfluential,â said Barbara Finamore, Asia director at the NewYork-based Natural Resources Defense Council.
August 27th, 2020 at 8:07 pm
Which university are you at? synthroid 225 mg A U.S. Department of Commerce official says the United States and U.S. investors would be willing to invest in the building of a canal across the middle of Nicaragua as long as the process is transparent.
August 27th, 2020 at 8:08 pm
What line of work are you in? synthroid 75 mg bula
The equipment was fitted within five years and as a result the speed of trains is monitored by a series of sophisticated grids on the track which can take over the control of the engine and slow it down.
August 27th, 2020 at 8:08 pm
We used to work together refissa tretinoin cream 0.05 reviews PALO ALTO, Calif. — The wall of Stanford players reacted in unison as the scene unfolded in front of their sideline late Saturday night. Their arms waist high and flailing, they tried to will an official’s call that would end the threat. If they waved their arms hard enough, Washington quarterback Keith Price’s worm-burner to Kevin Smith would be ruled incomplete. That would result in a turnover on downs, and the game would be over. The official closest to the play sprinted in, waving his hands above his head. He thought the pass complete.
August 27th, 2020 at 8:08 pm
This is your employment contract aspirina prevent Traders and petroleum marketers say the shutdown will causeshortages and higher prices for diesel and jet fuel in areasalong the pipeline as shippers scramble for supply and pay moreto have it sent by barge, rail or truck to customers.
August 27th, 2020 at 8:08 pm
Where did you go to university? brand name synthroid no prescription Bruckheimer told The Hollywood Reporter he is leaving the studio when his contract expires because he wants to make movies Disney isn’t interested in financing. He insisted he is not severing ties with the studio because their summer collaboration “The Lone Ranger” was a box-office flop.
August 27th, 2020 at 8:08 pm
I’ve only just arrived cialis 15 mg Prescott voters are choosing whether to re-elect a mayor who has helped lead the city in mourning the loss of 19 firefighters but also been criticized for his response to providing full benefits for each of the men’s families.
August 27th, 2020 at 8:08 pm
Another service? zanaflex dosage for migraines Three others took the aggregate suspensions to 70 years between nine conspirators.
August 27th, 2020 at 8:10 pm
What do you study? sleepwell mattress cost in chennai “We are inherently moving into new phase form the Chinese perspective. I think that is around the suitability of development. I think it is around the stability of development, I think the government is very focused on that,” he said.
August 27th, 2020 at 8:12 pm
On another call ventas de viagra Turkey wants to extract assurances from the PYD that it will not threaten Turkey’s security or seek an autonomous region in Syria through violence, and that it will maintain a stance of firm opposition to Syrian President Bashar al-Assad.
August 27th, 2020 at 8:15 pm
Which university are you at? buying xenical in australia So why are more and more people being diagnosed with thyroid cancer? âWe think the increasing incidence is due to better detection, not necessarily because more people are developing the disease,â says Teng. âAs imaging technology has gotten better and better, weâve been able to detect smaller and smaller nodules â which may perhaps lead to overdiagnosis of some thyroid malignancies that would never be fatal.
August 27th, 2020 at 8:15 pm
I work with computers precio abilify 5mg What happens when your government does nothing because a small minority uses the means of the filibuster as an act of obstruction? Your country inters into a dark-age.The right in this country is not conservative, far from it. It’s become doctrinarian and authoritarian in nature. True conservatives are practical people. While they want a smaller government, they want what they pay for to work. Today’s right doesn’t want government to work at all.True conservatives believe in using incentives to help and motivate people, incentives that work. Conservation and Conservative both come from the Latin, to conserve.Let’s restate what the Republicans have done. — They want to raise the costs for kids going to school, eliminate health programs, send our jobs overseas, cut corporate taxes, not worry about the environment, raise taxes on the So they think they can ramp up the misery, increase our fear and hatred of the very circumstances they have helped bring about through record filibusters, voter suppression efforts, saber rattling with Iran, etc.
August 27th, 2020 at 8:15 pm
I’m sorry, I didn’t catch your name albuterol buy uk
Balanced growth is seen as the holy grail by the government and the Bank of England. That means exports and investment playing a bigger part with less dependence on debt fuelled consumer spending which pushes up imports.
August 27th, 2020 at 8:15 pm
When can you start? mirtazapine 30 mg orodispersible tablets KKR’s latest Chinese milk deal comes just as the country’s top leaders are orchestrating an industry consolidation. The government’s effort stems in part from the 2008 tainted milk powder scandal that killed at least six babies and sickened thousands more.
August 27th, 2020 at 8:16 pm
We work together voltaren gel costco When Narendra Modi speaks, people listen. Itâs not just because heâs widely expected to be the opposition Bharatiya Janata Partyâs (BJP) candidate for prime minister in elections due in 2014. The chief minister of Gujarat seems to know his audience well. They cheer him on and jeer at his opponents; they applaud every two minutes. But sometimes, what he says catches peopleâs attention.
August 27th, 2020 at 8:16 pm
We need someone with qualifications havana club preis rewe “Our advice to UK Coal was they should consider stopping that particular face sooner rather than later, because they were heading for a geological fault,” said the chief inspector of mines, Steve Denton.
August 27th, 2020 at 8:16 pm
I’m a partner in pro agra 100 mg Republicans and their banking donors landed you in 17 trillion debt but as long as they have supporters like you voting them back in you’ll all be taken to the cleaners again and again and again. You voted for it, you deserve it.
August 27th, 2020 at 8:16 pm
Enter your PIN who should not take dapoxetine
âThere will be no letdown,â Ryan said. âIf the Pittsburgh Steelers beat us, itâs because they beat us. Thereâs no other factor because our focus is strictly on them. For us, we have to improve by leaps and bounds as a football team. We know there are a lot of areas we can improve in. Thatâs where our focus is. We learn from what happened, some of the things we need to correct and you move forward to your next opponent. Thatâs where weâre at.â
August 27th, 2020 at 8:17 pm
A few months is cialis over the counter in australia Another piece of good news for Mr Rouhani as he approaches his inauguration is the recent refusal of the UN Security Council to back a report by its investigative committee that concluded Iran has violated the sanctions.
August 27th, 2020 at 8:18 pm
I’d like to change some money albendazole dosage for toddler Though thecountry boasts the biggest union in the world, the All-ChinaFederation of Trade Unions (ACFTU), it is a state-run body thatcritics say regularly favours investors over workers.
August 27th, 2020 at 8:20 pm
I hate shopping combivent no prescription needed * Johnson & Johnson reported on Tuesday that itsearnings more than doubled in the second quarter of this year,buoyed by strong sales of prescription drugs and an influx ofcash from the sale of its stake in the Irish drug manufacturerElan. ()
August 27th, 2020 at 8:21 pm
Thanks funny site mvp gold 1800 mg review Now, prepare for that kind of eye-brain challenge when you vote in November, because the Board of Elections has reduced the type size on the ballot to near microscopic proportions. If you require glasses, which essentially covers anyone over 40 and plenty under, start practicing with the phone book.
August 27th, 2020 at 8:23 pm
Will I have to work on Saturdays? how long does it take for zyrtec to wear off However, it doesn’t necessarily mean there are more places available. Although last year saw a rise on the 500 or so students who entered university through adjustment in 2011, only 1,344 students landed their place through adjustment in 2012.
August 27th, 2020 at 8:24 pm
We work together combien ca coute du viagra Mobile service provider Sprint Corp posted a widerquarterly loss on costs from shutting down its Nextel network,but revenue grew as customers spent more on wireless services.Shares rose 2.3 percent in premarket trading.
August 27th, 2020 at 8:24 pm
Three years apo clomipramine 10mg Teresa Heinz Kerry’s condition has been upgraded from critical to “fair,” according to a spokesman, after the wife of Secretary of State John Kerry was rushed to a Massachusetts hospital over the holiday weekend.
August 27th, 2020 at 8:24 pm
What’s the interest rate on this account? weaning off of dilantin “If Homs falls, it will be very difficult for us to explain to the families of tens of thousands of dead Syrians why we negotiated with a regime that shows us day after day that it doesn’t want a political solution and that it only wants to kill more Syrians.”
August 27th, 2020 at 8:24 pm
Can I take your number? can you get addicted to motrin 800 This season sees the return of the matching suit, be prepared to see stores filled with printed, floral, graphic and monochrome identical skirts, trousers and blazers. Topshop are already all over this look and check out our other hot picks to see you into winter.
August 27th, 2020 at 8:24 pm
An envelope what is a prescription dose of benadryl It would be helpful to know the dates of when this survey was actually taken. In this particular instance, if the survey was taken at the time that the U.S. was seriously contemplating bombing Syria, then I could certainly appreciate the angst and pessimism. I would also be interested in learning how Director Curtin determined that the reading was largely influence by the fear of higher interest rates, and less enthusiasm in the housing markets. This may all be true, but I don’t know how the reasoning was established.
August 27th, 2020 at 8:24 pm
Could you please repeat that? coming off lexapro when pregnant
The broadsheet Frankfurter Allgemeine Zeitung ran a report on p.7, whilst the Sueddeutsche Zeitung newspaper carried a p. 10 report with the headline: ‘In memory of Diana: The remarkable christening of Prince George’.
August 27th, 2020 at 8:25 pm
Please call back later arcoxia 30 mg prospect According to the study, internalizing weight-based stereotypes, teasing and other stigmatizing experiences are linked to depression and binge eating. Stress, including heightened public awareness, is also linked to weight gain.
August 27th, 2020 at 8:27 pm
I’d like to pay this cheque in, please buy metanx online “Once at that location, officers went to the apartment, but couldn’t make contact
August 27th, 2020 at 8:29 pm
I study here online prescription drugs oxycodone Hengqin has been part of the central government’s plan todevelop the Pearl River Delta since 2008, and the island isbeing groomed as a test bed for political and economic projectsbetween the southern Guangdong province and the specialadministrative regions of Macau and Hong Kong.
August 27th, 2020 at 8:29 pm
I’ve been made redundant viagra sales figures 2019
According to the Congressional Research Service, the family of Hawaii Sen. Daniel Inouye, D-Hawaii, who died Dec. 17, 2012, was given $193,400. The family of Rep. Robert Matsui, D-Calif., who died on Jan. 1, 2005, was gifted $162,100, while relatives of Rep. Jo Ann Davis, R-Va., who died on Oct. 6, 2007, were given $165,200.
August 27th, 2020 at 8:31 pm
Whereabouts are you from? viagra purchase uk Blair Jenkins, chief executive of Yes Scotland which supports independence, said there are a number of policy areas that could swing the vote: âIssues of identity are playing only a small part in the debate. It is about what kind of country we want to live in and what kind of economy we want to be part of.
August 27th, 2020 at 8:32 pm
Could I make an appointment to see ? order trileptal Napolitano also called the use of expressions like “coup d’etat” and “subversion” when referring to Berlusconi’s conviction was “absurd”, and he repeated that neither he nor Prime Minister Enrico Letta could do anything to change the outcome of the trial.
August 27th, 2020 at 8:32 pm
I’ve come to collect a parcel acheter du viagra a toulouse USC has already lost two wide receivers for the season. George Farmer injured his knee during spring practice and freshman Steven Mitchell hurt his knee in June during a voluntary workout with teammates.
August 27th, 2020 at 8:32 pm
Who’s calling? ou acheter du viagra en securite You also can’t ignore the fact that he hasn’t actually spanked your child — right? Philosophies are important, yes, but not as important as what he does, and so far he’s just talking to you.
August 27th, 2020 at 8:33 pm
Where do you come from? orlistat otc uk “We did a lot of good things and when you put up that many runs you figured you stand a good chance to win,” said Toronto manager John Gibbons. “But if you look at that lineup over there they can burn you in so many ways and that’s what they did tonight.”
August 27th, 2020 at 8:33 pm
I’m training to be an engineer buy penomet australia A surprisingly sharp drop in initial U.S. weekly claims forjobless benefits to an almost six-year low and an inflationfigure for July that was in line with expectations supportedviews that the Fed will begin shifting its policy stance soonerrather than later, driving the dollar higher.
August 27th, 2020 at 8:34 pm
perfect design thanks 1000 mg of amoxicillin for strep Earlier this month, Twitter filed with regulators for aninitial public offering. Reuters reported last week that Twitterwas in talks looking to add additional banks to its underwritingsyndicate. (Reporting by Gerry Shih)
August 27th, 2020 at 8:36 pm
Other amount olanzapine uk The man accused of abducting and raping three women and holding them captive for years is due to appear in a Cleveland court today amid media reports that an agreement is in the works that would allow him to avoid the death penalty.
August 27th, 2020 at 8:37 pm
Good crew it’s cool amitriptyline cream 10
amitriptyline cream 10
The world’s biggest hamburger chain said global sales at restaurants open at least 13 months rose 0.7 percent last month, slightly more than the analysts’ average estimate of 0.4 percent, according to Consensus Metrix.
August 27th, 2020 at 8:39 pm
How do you spell that? amoxicillin clavulanate cost walmart On Aug. 20, 2012, Obama said, “We have been very clear to the Assad regime, but also to other players on the ground, that a red line for us is we start seeing a whole bunch of chemical weapons moving around or being utilized. That would change my calculus. That would change my equation.”
August 27th, 2020 at 8:40 pm
A book of First Class stamps where to buy viagra without prescriptions yahoo Marte Deborah Dalelv from Norway, 24, talks to the Associated Press in Dubai on Friday about how she was sentenced 16 months in jail for having sex outside of marriage after she reported an alleged rape.
August 27th, 2020 at 8:40 pm
I’m about to run out of credit tadalis anwendung As the sunken side of the vessel emerged from the water, engineers ceased the pressure from the cables and huge tanks fixed to the ship’s exposed side began filling with water, using the effect of gravity to pull the ship vertical.
August 27th, 2020 at 8:40 pm
What do you do for a living? buy topiramate online The top trade on Facebook on Wednesday was a 10,250-lot of September $39 strike puts, which were bought for 7 cents per contract as a new position. The contract, which is out-of-the-money, expires at the end of next week and would be profitable if shares fall below $38.93, Ruffy said.
August 27th, 2020 at 8:41 pm
Is there ? alli price walmart More than 300 medics were travelling the area to give residents check-ups and inform them on the outbreak, while the authorities had set up police checkpoints to enforce quarantine zones, the health ministry said.
August 27th, 2020 at 8:41 pm
I’d like to apply for this job suprax 400 mg capsule Amgen, the drugmaker in advanced talks to buy Onyx for $130 per share, or about $9.5 billion based on shares outstanding, had asked to see data from an ongoing trial on Kyprolis in order to better evaluate the treatment, people familiar with the matter said previously.
August 27th, 2020 at 8:42 pm
I read a lot wo kann ich viagra online bestellen A high-powered meeting of lawyers opposed to impending criminal legal aid cuts ended on Tuesday night without agreement on a date for industrial action, despite strong support in the hall for a vote on it.
August 27th, 2020 at 8:43 pm
Through friends viagra tablate how use in odia One of the most perplexing aspects of this decision is its timing. Taking such drastic action just before the start of a new school year, when parents are lining up at the clinics to get their children immunized, is particularly cold even for this administration.
August 27th, 2020 at 8:43 pm
Pleased to meet you doxepin goodrx
“It happened so quickly,” Grabner said after practice. “I was backchecking and at the last second I just started cutting over trying to interrupt a play and then I looked back and he was on the ice.”
August 27th, 2020 at 8:46 pm
Another year starting paxil reviews The White House, and federal agencies including the Department of Health and Human Services (HHS) and the Internal Revenue Service (IRS), must ensure that working marketplaces open for enrollment in all 50 states in less than 80 days, and are responding to mounting pressure by concentrating on three essential areas that will determine whether the most critical phase of Obamacare succeeds or fails.
August 27th, 2020 at 8:46 pm
Have you seen any good films recently? bactrim for uti
Cyclescheme founding director Richard Grigsby agreed there was “huge scope” to increase the popularity of commuting to work by bike - noting that, on average, only around 3% of employees in the large organisations he provided with cycle to work schemes took it up.
August 27th, 2020 at 8:47 pm
Could you ask her to call me? rumalaya crema precio Donate tickets to sporting events, theatres, and movies; specialty food items, health and beauty items; kitchen essentials; gift baskets; and gift certificates to grocery stores, pharmacies, and department stores.
August 27th, 2020 at 8:49 pm
I’m a partner in ginette ny
Francisco Garzon Amo, who suffered a bloody head wound in the crash that killed 78, is accused of suspicion of reckless homicide. Scores more of the 218 passengers were injured when the eight-car train, traveling well above the 50-mph limit in a turn, whipped off the tracks and crashed in the northwestern town of Santiago de Compostela.
August 27th, 2020 at 8:49 pm
The line’s engaged paxil buy canada Novellist is in great shape. He impressed again yesterday morning, working a brisk seven furlongs on Wohler’s home gallop at Ravensberg, situated between Dortmund and Hanover, giving great encouragement that he has held his form since winning the Grand Prix de Saint-Cloud last month.
August 27th, 2020 at 8:49 pm
How many weeks’ holiday a year are there? atorvastatin sandoz 20 mg
Amazon is the world’s largest online retailer and has a growing library of digital content. Consumers pay far less for Kindles than Apple’s iPad and Android tablets from Samsung Electronics. But those gadgets have far more applications, which many industry experts consider the most vital factor behind purchase decisions.
August 27th, 2020 at 8:49 pm
I’m interested in this position vigora 100 how to use in hindi The system operates in two steps: First, the device separates recorded cries into 12.5-millisecond frames, with each frame then analyzed within several characteristic parameters, including frequency, voicing and acoustic volume.
August 27th, 2020 at 8:50 pm
Punk not dead best place to buy viagra online uk There is no premium involved in the merger, althoughPublicis was slightly smaller in terms of market capitalisationthan Omnicom. A person close to the deal said that the dividendswere designed to bring the equity stakes to parity.
August 27th, 2020 at 8:50 pm
Would you like to leave a message? enalaprilmaleat Cavendish plays the ruthless ringleader of a vicious gang of outlaws in the $250 million western. Although there have been many portrayals of the character on screen, Disney is the first studio to present him as facially disfigured. Disney describes the character, who is played by William Fichtner, as “a ruthless outlaw whose terribly scarred face is a perfect reflection of the bottomless pit that passes for his soul.”
August 27th, 2020 at 8:50 pm
Sorry, you must have the wrong number lipitor buy online âWe are using investment dollars to pay currentoperational bills, and that approach is not without risk to ourlong-term effectiveness,â he said in the statement. âWe canâtmortgage our future.â
August 27th, 2020 at 8:52 pm
I came here to study trazodone 50 mg to get high âWe started by hearing gunshots downstairs and outside,â said Patrick Kuria, a worker at the mall restaurant Artcaffe. âLater, we heard them come inside. Then we saw two gunmen wearing black turbans. I saw them shoot.â
August 27th, 2020 at 8:53 pm
Enter your PIN buy deal online sale viagra viagra “Given what has already happened in England – where a court case is being brought against the Church of England with the ink barely dry on the Royal Assent – there is no doubt that we will see similar instances north of the Border.”
August 27th, 2020 at 8:55 pm
This is the job description whats the best generic cialis
With an eye on the 2014 congressional elections, both parties tried to deflect responsibility for the shutdown. President Barack Obama accused Republicans of being too beholden to Tea Party conservatives in the House of Representatives and said the shutdown could threaten the economic recovery.
August 27th, 2020 at 8:57 pm
I never went to university effexor xr coupons or rebate It said cash payments by adoption agencies to orphanages led them to seek out children for adoption, often without proper checks into their background or their family circumstances.
August 27th, 2020 at 8:57 pm
Could you send me an application form? www.spine-health.com/video/lumbar-radiofrequency-neurotomy-video President Obama’s Justice Department and lawmakers from the House and Senate — nearly all Republicans — filed legal briefs this week asking the Supreme Court to rule in favor of religious invocations at government meetings.
August 27th, 2020 at 8:57 pm
I’m unemployed buying viagra in tijuana mexico If you are unsure if law is right for you, hopefully these four questions will prove helpful. Speaking with current law students, professors and practicing attorneys will provide you with invaluable insights from those with direct experience in the law and in legal academia so that you can fully understand this important life decision.
August 27th, 2020 at 8:57 pm
I’d like to pay this in, please levitra per pay pal zahlen “They chose the films that wanted to tell something about the lack of love, about the lack of human relationships,” said Hungarian director and feature competition jury president Istvan Szabo.
August 27th, 2020 at 8:58 pm
I’m sorry, I didn’t catch your name dulcolax dosage uk On Sunday, a Cairo court announced that the top leader of the Brotherhood and two other officials including Shater would go on trial in three weeks’ time for crimes including incitement to murder during protests in the days before Mursi was toppled.
August 27th, 2020 at 8:58 pm
A law firm glucophage tablets what are they for The curriculum has also been backed by Michael Gove, the Education Secretary, who said it should be employed as a “national benchmark document by all those responsible for the RE curriculum locally”.
August 27th, 2020 at 8:58 pm
What line of work are you in? amoxicillin zyrtec generic drugs viagra rxpricebusterscom “There will be a push to be more efficient so that theairplanes fly more hours, we better manage maintenance, we workon how to have fuel savings as we fly,” Franke said in aninterview on Tuesday after the deal was announced.
August 27th, 2020 at 8:59 pm
I’m in my first year at university lipitor 10mg side effects “I ask the president of the Islamic Republic of Afghanistan to announce another person for this position,” said parliamentary speaker Abdul Rauf Ibrahimi after the ballot. Just sixty lawmakers backed Patang while 136 opposed him.
August 27th, 2020 at 9:01 pm
I’ll call back later himalaya himcolin cream That was a reference to the last-minute legislation that will fund the government only until Jan 15 and give Treasury the ability to borrow above the $16.7 trillion limit until Feb. 7 or a few weeks longer.
August 27th, 2020 at 9:01 pm
Which year are you in? viagra vs cialis vs levitra prices Rep. James Clyburn (D-SC); House Minority Leader Nancy Pelosi (D-CA); and Rep. Xavier Becerra (D-CA) speak to members of the media during a news conference in the Capitol on October 5, 2013 in Washington, D.C. (Photo by Chris Maddaloni/Getty Images)
August 27th, 2020 at 9:03 pm
Go travelling how to get zyprexa free For foreign banks, Lloyds’ sale is part of a wider trend ofWestern financial institutions retreating from Asia to focus ontheir home markets. European and U.S. banks have also beenshedding non-core Asian operations to bolster their balancesheets to comply with new Basel III capital rules.
August 27th, 2020 at 9:04 pm
I came here to work erexin-v online California Governor Jerry Brown, a Democrat, had asked the court to overturn a lower court ruling that requires the state to reduce overcrowding to 137.5 percent of design capacity. The state says it might have to release up to 9,000 prisoners by the end of the year to be in compliance.
August 27th, 2020 at 9:06 pm
I’m on business how to buy viagra over the counter “In light of the issues that have been raised surroundingthe use of propofol in executions, I have directed theDepartment of Corrections that the execution of AllenNicklasson, as set for October 23, will not proceed,” Nixon saidin a statement.
August 27th, 2020 at 9:06 pm
Through friends differin adapalene 0.1 The casualties came fast and were ferried into the nearby al-Fateh mosque. Inside, families crowded around their loved ones, fashioning makeshift tourniquets in desperate attempts to stem the blood from their wounds.
August 27th, 2020 at 9:06 pm
I can’t get a signal amoxicillin overdose in dogs A day after Gamblero, 38, suffered fatal injuries from falling out of a two-story apartment window in Queens, players recalled his positive energy and unique fashion sense that included neon-colored game day outfits.
August 27th, 2020 at 9:07 pm
I’m afraid that number’s ex-directory cheap kamagra 50mg “I gave a prediction to our board, which is myself and Lord Sugar, and I’m ahead of that prediction so from my perspective that’s good. The business plan I proposed on The Apprentice has been robust enough to survive this first year.” Stylfile has made profits of £28,000 on a turnover of between £250,000 and £300,000 and Pellereau says there’ll be more this year. He drives a BMW and has just moved into his first house with his wife and their new daughter.
August 27th, 2020 at 9:07 pm
I want to make a withdrawal acheter viagra en ligne danger
Miley Cyrus complains about the paparazzi, and yet with each passing day, she’s spotted out and about flaunting her body in outfits that just scream “look at me!” From short shorts to see-through tops…
August 27th, 2020 at 9:08 pm
Languages grc*triverex 3 Grantham, 74, recalls being knocked unconscious five times in one season with the Jets. “Usually the trainers would leave it up to the player, even though we had team doctors and orthopedic men on the sidelines,” he said. “Most times the trainers took our word.”
August 27th, 2020 at 9:08 pm
I read a lot is it possible to get pregnant while taking clomid Although a majority of students support civil rights and protection policies for lesbian, gay, bisexual and transgender people, a significant amount remain neutral or opposed to certain ideas, such as same-sex marriage and civil unions, according to a new study from the University of Michigan.
August 27th, 2020 at 9:10 pm
Insert your card alli 120mg uk Cooper spoke to the media again after practice Thursday, telling them his meeting with teammates a night earlier was “extremely emotional.” Teammates Michael Vick, Jason Avant and others expressed forgiveness for Cooper. LeSean McCoy also said he forgives Cooper, but “I can’t really respect somebody like that.”
August 27th, 2020 at 9:12 pm
One moment, please sildalis sildenafil For about an hour, the jobseekers brainstorm. The founders of Airwoot â which manages companies’ responses to what customers are saying about them on social media â troll for ideas about customer data that their clients would find most useful. Another firm, Learning Outcomes, seeks help getting Indian schoolteachers to adapt their grading techniques to facilitate the company’s performance evaluation software. iDubba looks for tips on improving the chat rooms on its TV guide app.
August 27th, 2020 at 9:12 pm
Have you got any experience? cialis nhs price The U.S. and China introduced a new round of sanctions against North Korea at the United Nations that the U.S. said would significantly impede the development of Pyongyang’s nuclear and missile programs, in response to its test last month of an atomic bomb.
August 27th, 2020 at 9:15 pm
We’ll need to take up references duloxetine for migraine Aaron Rodgers was sacked 51 times last year and the Packers averaged a dismal 3.9 yards per carry. Even worse, that average would be lower had it not been for Rodgers’ mobility as he hit 4.8 per attempt. No ball-carrier with 70-plus carries averaged more than 3.6.
August 27th, 2020 at 9:15 pm
A financial advisor plavix online coupons
The Giants will open training camp on Friday in the shadow of the site of Super Bowl XLVIII, yet theyâre barely seen as a true candidate to reach that final game at MetLife Stadium. The 49ers and Seahawks are widely considered the NFCâs finest, and all the NFC East hype centers around Chip Kellyâs new offense in Philadelphia and Robert Griffin IIIâs rapid recovery in Washington.
August 27th, 2020 at 9:15 pm
I’m sorry, she’s purchase trental online
The OFT has not reached a decision as to whether there has been an infringement of competition law. In light of Amazon’s decision, however, the OFT is currently minded to close its investigation.
August 27th, 2020 at 9:15 pm
How do you know each other? coreg cr 20 mg capsule The poll finds that 65 percent of independents think Congress should keep working on the law, up from 53 percent last year. Itâs noteworthy that 41 percent of Democrats now feel the law needs more work, up from 35 percent.
August 27th, 2020 at 9:15 pm
Jonny was here plant based diet guide pdf The scale of the challenge is significant. According to theLondon Stock Exchange, the 246 tech companies listed onBritain’s stock markets total $200 billion in capitalisation,compared with $3.2 trillion in the U.S. Meanwhile, investment inLondon-based tech groups is falling, due possibly to a loss ofappetite for the kind of consumer internet companies the citytends to produce. Some 24 London-based companies pulled in 62million pounds in the first quarter of 2013, less than half the151 million pounds raised by 29 companies in the final quarterof last year, research from market tracker Ascendant shows.
August 27th, 2020 at 9:15 pm
I’ve just started at what color are viagra pills Reuters on Aug. 13 reported that JBS USA, prior to Tyson’sannouncement, played short video clips at an industry conferenceshowing cattle fed beta-agonists that were reluctant to move andstepping tentatively as if on hot metal.
August 27th, 2020 at 9:16 pm
I’m doing an internship buy alesse online without prescription Yet it’s Redmayne, a front-runner for this year’s Best Actor Oscar for “The Theory of Everything,” who fares worst
August 27th, 2020 at 9:16 pm
I’d like to take the job can you get high off of zantac 75 âThe good news is that weâre not seeing any activity,â said David Litke, environmental health director for the Waco-McLennan County Public Health District. âWeâve still got to get through September. Once cooler nights hit consistently, the mosquito activity drops off. But people have to remember, we still have mosquitoes year-round.â
August 27th, 2020 at 9:19 pm
How many more years do you have to go? lansoprazole 40 mg
With 7 percent of S&P 500 companies having reported, 52.8percent have reported profits that topped expectations,according to Thomson Reuters data, below the historical averageof 63 percent. There have also been fewer companies beatingrevenue forecasts this quarter.
August 27th, 2020 at 9:19 pm
Is there ? buy prexil uk
Germany’s Daimler posted a strong month as well,with sales of its Mercedes-Benz luxury brand increasing nearly14 percent after the French government was forced to end itssales ban of certain vehicles.
August 27th, 2020 at 9:21 pm
Have you read any good books lately? viagra en gotas para hombres The Jets share that contempt for an organization that has repeatedly bludgeoned them. Antonio Cromartie famously called Tom Brady an âass—-â a few years ago. Darrelle Revis once voiced his displeasure about Belichick. The Jets, of course, tattled on New England to introduce the world to Spy Gate.
August 27th, 2020 at 9:23 pm
I’d like to cancel a cheque clotrimazole topical solution drops Time continued to take from Terri Hernandez. She lost her first husband, Dennis, to complications from hernia surgery in January 2006, and later married Jeffrey Cummings, a landscaper who slashed a three-and-a-half-inch laceration on her right cheek with an eight-inch knife blade. That occurred in her house on June 29, 2010. He pushed her to the ground, held the knife to her throat and stabbed the knife into a chair she sat on, according to a police report. Officers arrested Cummings in the backyard, where Dennis and her sons once held football battles. The couple later divorced.
August 27th, 2020 at 9:23 pm
I’m in a band pharmaplus.com.br Successful Dan drew the rail in the eight-horse field and was installed at 12-1 on the morning line coming off a fourth-place finish in the Stephen Foster, won by Fort Larned at Churchill Downs on June 15.
August 27th, 2020 at 9:23 pm
The manager lopressor sr half life That is a small group relative to the more than 1 million total advertisers that Facebook counts, but analysts say that app developers represent an attractive and growing group of customers for Facebook to tap into. Smartphone apps, designed for Apple Inc’s iPhone or Google Inc’s Android-based phones, have struggled to stand out in a crowded field.
August 27th, 2020 at 9:23 pm
I read a lot on 30 mg celexa racing thoughts A second set of settlements includes $80 million of payments for billing of credit-card customers for identity-theft protection services that they did not receive. The deals, made with the U.S. Office of the Comptroller of the Currency and the Consumer Financial Protection Bureau, come after the company issued $309 million of refunds to customers.
August 27th, 2020 at 9:24 pm
Could I have , please? trazodone order Although most say theyâve come to find jobs and escape poverty and discrimination at home, the visible presence of Roma begging on sidewalks or in subway cars, complaints from the neighbors of Roma camps, and media reports of migrant involvement in petty crime have fueled a public and political backlash.
August 27th, 2020 at 9:24 pm
A few months levitra online buy White House spokesman Jay Carney called it “a hard fact of war” that U.S. strikes sometimes result in civilian casualties, but said drone strikes did so far less than conventional attacks. The United States takes pains to make sure any such strikes conform to domestic and international law, he said.
August 27th, 2020 at 9:25 pm
Very Good Site dosage for ibuprofen 600mg âI wanted to come back out there,â said Kuroda, who threw 90 pitches, not counting the estimated 20 additional tosses during the rain delay. âI gave (pitching coach) Larry (Rothschild) a hard time.â
August 27th, 2020 at 9:26 pm
Where are you from? doxycycline syrup for cats Wilson finished 24 of 34 for 258 yards and touchdown passes of 39 yards to Ricardo Lockette and 5 yards to Lynch, both late in the first half
August 27th, 2020 at 9:26 pm
I’m a housewife condom manforce image âAs far as ruling anything out, I havenât even, to be honest with you, thought about anything past today,â Anthony said on Saturday in Queens, where he was hosting a youth camp. âMy mind is not even thinking about next season, next offseason right now. Iâm just trying to do what I do this offseason to get right, work out, train and get right and prepare myself for this season. When that time comes, Iâll deal with that.â
August 27th, 2020 at 9:28 pm
Will I have to work shifts? can you buy permethrin 5 over the counter Berlusconi’s lawyers have appealed to the European Court ofHuman Rights to strike down the so-called “Severino law” whichbans politicians convicted of serious criminal offences fromparliament and the PDL wants the Senate committee to delay anyvote while the court decide.
August 27th, 2020 at 9:30 pm
Could I take your name and number, please? keflex price rite aid The ordeal, which began Friday evening and kept the apartment complex an active crime scene throughout the night, began when Vargas, 43, set fire to the apartment he shared with his mother, Zogby said.
August 27th, 2020 at 9:30 pm
Who’s calling? abilify generic name For the locals, the floods were more than just a natural disaster. A priest told us that the government had angered the Gods and brought this disaster upon the people. According to legend, he said, the Char Dham pilgrims were protected by Dhari Devi (an avatar of the Hindu goddess Kali Mata). However, the idol had been shifted from its original place in view of the Hydel Power Project.
August 27th, 2020 at 9:32 pm
Could I ask who’s calling? neurontin cost walmart
Bank Vontobel, which had forecast 2 billion Swiss francs ($2.05 billion) in peak sales from aleglitazar, pruned its price target for Roche to 263 francs, from 270 francs, after the setback but confirmed its “buy” rating.
August 27th, 2020 at 9:32 pm
Good crew it’s cool imitrex 6 mg/0.5 ml sub-q The Coalition wanted to introduce new rules to stop multiple exam boards competing to offer tests in the same subject, although these proposals were also shelved because they fell foul of EU competition laws.
imitrex 6 mg/0.5 ml sub-q The Coalition wanted to introduce new rules to stop multiple exam boards competing to offer tests in the same subject, although these proposals were also shelved because they fell foul of EU competition laws.
August 27th, 2020 at 9:33 pm
Three years acheter viagra en chine The decision to file suit comes after the United Nations said earlier this year that it would not pay hundreds of millions of dollars in compensation claimed by cholera victims in impoverished Haiti, where the epidemic has killed over 8,300 people and sickened more than 650,000 since October 2010.
August 27th, 2020 at 9:33 pm
Are you a student? buy cheap amoxicillin online As the No. 2 wireless provider in the United States, AT&T has been looking to grow in a mature market and has beenurgently seeking access to additional wireless spectrum. It hasheld talks to buy smaller rival Leap Wireless International lastyear, Reuters reported.
August 27th, 2020 at 9:34 pm
I’ve just graduated mrsa treatment bactrim dose
A decade ago, he headed development of technology used in Intel’s Centrino platform, which led to the widespread adoption of Wifi technology that freed computer users from using cables to connect to the Internet.
August 27th, 2020 at 9:34 pm
I need to charge up my phone sam’s club propecia cost WASHINGTON, Oct 11 (Reuters) - The final stage of thelong-delayed U.S. farm bill is about to begin, but drafting alegislative compromise between the Senate and House ofRepresentatives is still hampered by deep partisan divisionsover cuts in food stamps for the poor.
August 27th, 2020 at 9:37 pm
I’m interested in this position over the counter bactroban Nor is he likely to pitch into the eighth or ninth inning unless his pitch count is unusually low.
August 27th, 2020 at 9:38 pm
I’d like to send this parcel to zanaflex 2mg reviews Most people don’t know anything about Google Glass and don’t care. A few know all about it and still don’t care. I’ve been accosted several times by people who’ve heard about it and want to try it on or want me to explain what it does and how it works.
August 27th, 2020 at 9:38 pm
I’d like to speak to someone about a mortgage adapalene cream over the counter AMR’s management had initially wanted to exit bankruptcy on their own, and only agreed to the US Airways deal under pressure from creditors. But AMR has a fiduciary duty to create the most value for its bankruptcy estate, which people involved in the bankruptcy said means supporting the merger.
August 27th, 2020 at 9:39 pm
Could you ask her to call me? cost of generic geodon Her father agreed to go into therapy, though she isnât sure he actually will. Her mother has channeled her buying instincts into a shopping blog. A little over a year ago they moved into a new house. A cleaning person comes regularly.
August 27th, 2020 at 9:41 pm
How much will it cost to send this letter to ? fluconazole discount
Fifth, there is a much larger issue at stake for the US in Syria â it is also a test of our global leadership. We are the undisputed world leader due to our economic, military and political might. We are, in the words of Princetonâs John Ikenberry, the âsystem operatorâ of the international order. Together with other major powers over the last century, we have created laws, rules and codes of behavior that all nations must honor. The US is the enforcer and the hub around which the system is regulated. Without American energy, attention and action, the world order cannot function well.
August 27th, 2020 at 9:41 pm
Best Site Good Work propranolol hydrochloride 10mg “Every day he came in, he was a great teacher. He helped out a lot of our young guys, not only our Latin guys, but everybody. He really taught a lot these guys how to play the right way as far as how on the field goes.”
August 27th, 2020 at 9:42 pm
I sing in a choir vaso ultra uk
The pending plan, which was approved by creditors in earlyOctober, relies on a planned $1.9 billion sale of new sewersystem bonds to replace soured bonds at the heart of what hadbeen the biggest U.S. municipal bankruptcy case until Detroitfiled for bankruptcy in July.
August 27th, 2020 at 9:42 pm
Is this a temporary or permanent position? walmart campbell pharmacy hours lunch SEATTLE â A few things will be different at this year’s Hempfest, the 22-year-old summer “protestival” on Seattle’s waterfront where tens of thousands of revelers gather to use dope openly, listen to music and gaze at the Olympic Mountains in the distance.
August 27th, 2020 at 9:43 pm
How do I get an outside line? buy cheap super p-force Bassist Jared Hasselhoff of the American rock group Bloodhound Gang is seen pushing the Russian white-blue-red tricolor flag into the front of his pants during a concert in the city of Odessa Thursday.
August 27th, 2020 at 9:44 pm
How do you do? 300 mg seroquel for sleep Activity in Chicago’s 165-year-old open-outcry grain markets has been declining for decades because of computerized trading, which can be executed much faster. But after the CBOT changed the way it reports end-of-day prices in June last year, the share of trading attributed to shout-and-gesture trading fell by about half.
August 27th, 2020 at 9:46 pm
I’d like to cancel a cheque how much does depo provera cost in canada The first page was addressed to his wife. The soldier hoped she wouldnât find it âsillyâ that he was writing to a baby. The next two pages were dedicated to his “darling” daughter. He warned her that she may not see him “for some time,” but he wanted her to know that she was loved.
August 27th, 2020 at 9:47 pm
About a year mrsa and bactroban Martin Boon, director of research at ICM Unlimited, said politics was undergoing “a period of unprecedented uncertainty”, with just over 100 days left until Polling Day on May 7.
August 27th, 2020 at 9:47 pm
Sorry, I ran out of credit how long does rogaine take to work As a consequence, the word of the United States no longer can be trusted in international climate negotiations. By meeting an emissions reduction goal, the US would have a bit of moral ground to stand on when asking other countries to do so as well.
August 27th, 2020 at 9:48 pm
The line’s engaged tetracycline 500mg dosage “When you look at the buyers of semiconductor equipment;when you look at the people who are really making very advancedchips these days, it’s a very small number,” Mike Splinter,Applied Materials’ executive chairman, told Reuters. “Technologychanges are getting more difficult and complex.”
August 27th, 2020 at 9:49 pm
International directory enquiries buy african superman pills uk
The dollar index, which tracks the greenback’s performanceagainst a basket of major currencies, last stood at 81.884, about 0.2 percent above late U.S. levels but still notfar from a low of 81.407 touched on Wednesday.
August 27th, 2020 at 9:49 pm
ventolin tablet 4mg
August 27th, 2020 at 9:50 pm
Yes, I love it! where can you buy accutane online
JPMorgan said on Aug. 7 that its mortgage-bond sales practices were under criminal investigation by U.S. prosecutors in California. The company has been discussing a potential $11 billion deal with state and federal authorities to settle that case as well as other related investigations, a person with knowledge of the talks said last month.
August 27th, 2020 at 9:50 pm
Please call back later does tetracycline make acne worse at first The agency, which handles about 140 surrogacy cases a year,65 percent of them for clients outside the United States, isopening an office in California to better serve clients fromAsia which has easier flight connections with the West Coast.Weltman said he hopes to hire a representative in Shanghai nextyear.
August 27th, 2020 at 9:51 pm
Who do you work for? trental 100 mg
Nevertheless, she’s under pressure at home after a wave of national protests against government corruption and poor public services, while Brazilians share the sensitivities of many Latin Americans fostered by a history of the USâ often heavy-handed interventions in the region.
August 27th, 2020 at 9:52 pm
We’re at university together buy proscar cheap Tuesday’s decline put the S&P 500 on track to break aneight-day string of gains. Nine of the 10 S&P 500 industrysector indexes fell, with energy and material shares rankingamong the day’s worst performers. Marathon Petroleum dropped 4.1 percent to $70.13. Alcoa slid 1 percent to$8.09.
August 27th, 2020 at 9:52 pm
I like it a lot malegra dxt uk The brief chicken nugget exploration was not meant to be an exposé of the chicken industry or fast food generally, but to remind consumers that “not everything that tastes good is good for you,” deShazo said.
August 27th, 2020 at 9:53 pm
I’d like some euros non prescription bactrim Sales of existing homes, a much larger category than newhomes, surged to a three-year high last month. Some analystsspeculated, however, that home buyers rushed into the market tolock in mortgage rates before they rose further.
August 27th, 2020 at 9:56 pm
I can’t get a signal clotrimazole cream ip 2 w/w âAbsolutely,â Mara told the Daily News back on that summer day. âI remember when Ernie (Accorsi) and I were going through those interviews back in 2004. Thatâs the one thing I was jealous of Pittsburgh. Bill Cowher had been there for so many years. I wanted to have that stability here.
August 27th, 2020 at 9:56 pm
Have you got a telephone directory? side effects of caverta 100 “The footage we get will allow millions of people from all over the world to see our canals, rivers and towpaths, and will hopefully encourage some people to make a trip to see them.”
August 27th, 2020 at 9:57 pm
How many days will it take for the cheque to clear? sleepwell durafirm spine care mattress review Speaking after his talks with Zarif, British Foreign Secretary William Hague welcomed Iran’s statements that it wants to improve relations with the West and ease concerns about its nuclear program, but he said words alone would not be enough.
August 27th, 2020 at 9:57 pm
Did you go to university? cheapest price for amoxicillin Treasury Department unveiledharsher-than-expected changes late last month to its existingrule book for on corporate “inversions,” which have become acause of concern in Washington about the threat posed to theU.S
August 27th, 2020 at 9:59 pm
Good crew it’s cool avanafil australia
avanafil australia
In 1999, construction of the first McDonaldâs stopped due to protest and the subsequent passage of a government law that bans franchised restaurants in the country. During the fight to pass the law, one person spearheading the drive against McDonald’s wrote in the local press: “It is not Bermudian. McDonald’s cheapens wherever it goes.”
August 27th, 2020 at 9:59 pm
I’d like to open a business account australian kangaroo pills What became of Salo, by the way? He died two years later, hit by a flying baseball while on duty at a local game. There’s a moral in there somewhere, but I’ll be damned if I know what it is. Team news to come.
August 27th, 2020 at 9:59 pm
Just over two years benzoyl peroxide cream medscape
You and most unionists believe that “wealth”, as used above, is money. That is simply not true. “Wealth”, as used above, is GROSS INCOME. Workers have NO CLAIM WHATSOEVER to any part of GROSS INCOME. GROSS INCOME merely indicates the economic size of a business.
August 27th, 2020 at 10:01 pm
I’m at Liverpool University children’s ibuprofen dosage for adults To be sure, Thompson is a capable politician who could find a way to close the gap in this race by election day. Heâs loved by many and he knows the important political clubs in the city about as well as anyone. Weinerâs campaign could implode. Quinnâs support, which eroded over months, could continue to melt away. Other candidates could get indicted. (This is New York, after all.)
August 27th, 2020 at 10:01 pm
I’ve lost my bank card celebrex cheaper alternative MRPL and Hindustan Petroleum had stopped purchasesdue to difficulties getting insurance for refineries processingIranian oil, forcing New Delhi to look at providing its ownreinsurance after European firms backed out over sanctions.
August 27th, 2020 at 10:01 pm
I’m not sure acyclovir 800 mg uses Revenues at what is the world’s largest bank by assets, climbed 13pc to $26bn during the quarter, as the company held onto its position as the biggest earner of global investment banking fees. That boost included an 18pc increase in trading revenues to $5.37bn, after a fall in the price of bank debt fuelled a better performance in credit and equities products.
August 27th, 2020 at 10:02 pm
I love this site can dogs have tylenol “I know about budgets. I was a drug dealer,” he said. “To be in a drug deal, you need to know what you can spend, what you need to re-up. Or if you want to start some sort of barbershop or car wash–those were the businesses back then.”
August 27th, 2020 at 10:05 pm
Which university are you at? cheap alternative to zovirax “She had 17,000 mutations in her tumor that were not found in her normal cells,” Solit said. After months of analyzing 140 mutations that were considered suspects, two of them - genes named TSC1 and NF2 - stood out.
August 27th, 2020 at 10:06 pm
I’m on business taking zyrtec while trying to conceive He and other analysts have also said Nokia needs to step up advertising and promotion of its phones. Many have said telecom carrier partners, particularly in the United States, have failed to promote Nokia to their customers.
August 27th, 2020 at 10:06 pm
Can you put it on the scales, please? diclofenac sodiu âYou spend years developing this craft,â says Esposito, who turned 55 this year. âWhen Iâm not working, Iâm an observer of life. When you are fortunate enough to get the opportunity, you want to get it right.â
August 27th, 2020 at 10:07 pm
We need someone with experience norfloxacin 400mg how to take A spokesperson for the company said:“once they have finished the scheme and secured a position within the business, successful apprentices can expect to earn upwards of 24k, depending on the exact role they go into”.
August 27th, 2020 at 10:08 pm
We’d like to offer you the job clomid 50mg success stories However, a better-than-anticipated Australian jobs reporthelped lift the market from session lows, while investors alsocheered President Barack Obama’s nomination of Federal ReserveVice Chairwoman Janet Yellen to run the U.S. central bank.
August 27th, 2020 at 10:08 pm
We work together tamsulosin beta 0 4 mg retard nebenwirkungen * The Delaware Supreme Court on Thursday unanimouslyreversed a lower court ruling on Activision Blizzard Inc’s move to buy back most of Vivendi SA stake inthe video game maker for $8.2 billion, letting the transactionmove forward. The deal is now expected to close next week. ()
August 27th, 2020 at 10:09 pm
This is the job description do i need a prescription for amoxicillin uk PARIS, Oct 15 (Reuters) - French investment bank Natixis is set to announce a plan to cut 700 jobs by 2015 aspart of a drive to reduce costs, according to two union sourcesand documents obtained by Reuters.
August 27th, 2020 at 10:09 pm
I didn’t go to university order acyclovir cream Senior administration officials described the corporate tax proposal as the first new economic idea Obama plans to offer in the coming months, with budget deadlines looming in the fall. Administration officials wouldn’t put a price tag on the proposal or say how much would be a “significant” investment in jobs since the dollar figures would be part of negotiations with Congress. But in an example from this year’s State of the Union address, Obama proposed $50 billion to put Americans to work repairing roads and bridges and other construction jobs.
August 27th, 2020 at 10:10 pm
one of our guests recently recommended the following website
August 27th, 2020 at 10:10 pm
Which year are you in? is zyrtec d available by prescription ** Seadrill, the world’s biggest gas and oil rigcompany by market capitalisation, is to sell part of its NorthAtlantic Drilling subsidiary to take on a strategicpartner with expertise on Arctic operations.
August 27th, 2020 at 10:10 pm
I want to report a buy viagra over the counter uk Responsible decisions will be taken to cure âthe health ofthe president and not expose her to a greater risk like thedemands of this work,â Scioli told a local radio station,according to La Nacion. âWe must continue with all our work andthe management agenda.â
August 27th, 2020 at 10:10 pm
Enter your PIN where can i buy generic effexor xr Despite the Islandersâ struggles, the 14,689 on hand seemed genuinely into it, shouting in unison with their usual collection of chants from the Coliseum, including a not-so-flattering one aimed at the crosstown rival Rangers.
August 27th, 2020 at 10:13 pm
I saw your advert in the paper topamax prescription coupon Earlier this year, the city weighed whether to hold a lottery for people interested in the exam, but officials backed away from that plan. The current list of eligible hires â those who already passed the exam and are waiting for their number to be called â already counts more than 25,000 names.
August 27th, 2020 at 10:15 pm
Until August buy levothyroxine 100 mcg “A lot of people usually throng roadside markets in Parachinar before sunset for Iftar (dinner) shopping,” said tribesman Haider Ali. “Hundreds of people were present during the blasts and that’s why the death toll was high.”
August 27th, 2020 at 10:17 pm
How much is a Second Class stamp? buy tylenol with codeine #3 in canada Cruz also refused to rule out the possibility that he could return during the preseason. On Monday, a source had indicated that Cruz would be rested for the final two exhibition games, but Cruz said “we’ll see.”
August 27th, 2020 at 10:18 pm
Yes, I play the guitar mirtazapine buy uk As the relentless violence ascribed to militant Islamist group Boko Haram continues to claim lives and destroy livelihoods, the blame game as to who is responsible for the failure to stop the bloodbath has gone into higher gear.
August 27th, 2020 at 10:18 pm
I went to how to make money selling drugs online latino Humphrey developed the trap in collaboration with Wisconsin-based Tomahawk Live Trap, which is working on a licensing agreement to sell the traps along with other snake-handling equipment such as tongs, hooks and secure bags.
August 27th, 2020 at 10:19 pm
Do you play any instruments? generic atorvastatin price But he said that procedures to defend certain assets of strategic importance, even for companies that were not state owned, could be implemented more quickly, adding governance rules for the fixed-line network needed to be changed.
August 27th, 2020 at 10:19 pm
How do I get an outside line? discount seroquel xr Obama met Senate Republicans at the White House and spoke byphone to House of Representatives Speaker John Boehner asnegotiations intensified on how to get hundreds of thousands offederal workers back on the job and extend the government’sborrowing authority past the Oct. 17 limit.
August 27th, 2020 at 10:19 pm
I’m afraid that number’s ex-directory 600 mg motrin get you high VMware sells virtualization software, which enables thecreation of a virtual machine that acts like a real computerwith an operating system. This helps companies use server andstorage space more efficiently and reduce IT costs.
August 27th, 2020 at 10:20 pm
We need someone with experience naproxen sodium buy uk This comes from our ad serving technology and is used to track how many times you have seen a particular ad on our sites, so that you don’t just see one advert but an even spread. This information is not used by us for any other type of audience recording or monitoring.
August 27th, 2020 at 10:24 pm
Have you got any ? how many seroquel does it take to overdose “We don’t think the U.S. will compromise on that, because past experience of abandoning Afghanistan was that the country descended into chaos,” the official said, recalling the bitter civil war that raged after the 1989 Soviet withdrawal and subsequent toppling of the Soviet-backed government of Mohammad Najibullah in 1992.
August 27th, 2020 at 10:26 pm
I live here isotretinoin 10mg dosage Earlier on Thursday, 14 militants died in two drone strikes in the central Yemeni province of Maarib. At least 28 al Qaeda suspects have been killed by drones in the past two weeks, a marked increase in the frequency of such strikes.
August 27th, 2020 at 10:27 pm
I’m a trainee price of viagra in brazil In a statement posted Wednesday on the Russian Foreign Ministry website, Lavrov was quoted as being asked specifically about the American insistence on Chapter 7 consequences, saying only: âWe are working within the framework of what was agreed on in Geneva.â
August 27th, 2020 at 10:27 pm
Who do you work for? cialis 10mg prix pharmacie The whole application process can be finished in under 10 minutes. Mr Chandrasekera said that applicants were given a fast service: “Our online payday loan facility is exactly the same as any other payday loan service. People can apply for the loan, get the decision there and then, and then get the money within a couple of hours.”
August 27th, 2020 at 10:27 pm
Could I borrow your phone, please? butea superba australia Freelancer matches employers and freelancers around the world through its website for tasks such as data entry, design and accounting. So far, it has had almost nine million users, with almost five million projects posted.
August 27th, 2020 at 10:28 pm
Will I get paid for overtime? super p force in singapore Despite the Obama administration’s assertion that “stand your ground” laws are a new concept in self-defense, they are in fact founded in common sense, natural law, and are well enshrined in American jurisprudence.
August 27th, 2020 at 10:28 pm
I really like swimming is trazodone hydrochloride a barbiturate The department also released a report Wednesday that charged Ferguson’s police department with routine racial discrimination.
August 27th, 2020 at 10:28 pm
What do you do for a living? doxepin canine The hunger strikers, who are also refusing work assignments, are protesting what prisoner advocates describe as the state’s inhumane solitary confinement practices, which can include locking inmates in isolated cells for up to 23 hours a day.
August 27th, 2020 at 10:29 pm
I came here to work viagra in indian market Republicans still want changes to the Affordable Care Act, but many are calling for additional cuts in government spending and other changes as the calendar is forcing a combined vote to end the shutdown and extend the debt ceiling.
August 27th, 2020 at 10:33 pm
Special Delivery trend micro titanium maximum security 2012 crack keygen “Brad was my first choice,” Ainge said. “I have watched and admired his poise, his intelligence, his teams, their effort, their execution under pressure. I’ve always looked at him the last few years as a guy that was a great candidate to be a head coach, never really thinking it was going to be this soon in Celtics history but is a guy that I have targeted for a long time as a potential great head coach.”
August 27th, 2020 at 10:35 pm
I wanted to live abroad cheapest lamisil tablets
‘We’d all like to thank Gov. [Andrew] Cuomo,’ said Scott Barocas, second from left. At far left is James Tancredi. From right are James Sullivan, Lawrence Sullivan Jr., Robert Sullivan, Michael Sullivan and John Sullivan. All are sons of FDNY first responders.
August 27th, 2020 at 10:36 pm
A staff restaurant diclofenac dietilamina gel para que sirve Strong new orders in October drove the biggest expansion inChina’s manufacturing sector in seven months, according to apreliminary Markit/HSBC survey of purchasing managers, providingfurther evidence the economy was stabilising.
August 27th, 2020 at 10:36 pm
Please call back later vibrox capsules 100mg doxycycline The Moto X will also be constructed in the United States, a factor that Motorola has already highlighted in its newspaper advert that ran just before July 4th. The company says that the Moto X will be the first phone that has been “designed, engineered, and manufactured” in the United States, but the manufacturer will have to wait and see if customers will respond to the patriotic tone.
August 27th, 2020 at 10:36 pm
Where do you live? dapoxetine hcl kaufen At the behest of city lawyers, Orr refused to answerquestions about any communication with the state. The Detroitchapter of the American Federation of State, County andMunicipal Employees filed a request with the court Wednesday toforce Orr and other witnesses to testify on communications frombefore the filing.
August 27th, 2020 at 10:36 pm
I’ll send you a text avis sur pharmacy.viagranow.eu “Now 37 and 38 weeks is called early term,” says McCabe. “Even at that point, the risk of a baby dying is 1.5 times as great as full term. Why put the baby at risk?” The American Congress of Obstetricians and Gynecologists recommends a policy called hard stop at 39 weeks. It means no elective inductions or C-sections should be planned before 39 weeks gestation.
August 27th, 2020 at 10:37 pm
A few months vigora 100 tablet information in hindi Although Fed officials have indicated October should not be ruled out, Marey said they would probably wait until December, after the outcome of another round of political battles on Capitol Hill over the debt ceiling.
August 27th, 2020 at 10:37 pm
Gloomy tales switching from paxil cr to effexor xr When jurors are given their instructions Friday, Zimmerman will face second-degree murder and manslaughter. But Judge Nelson said she needed time to mull over the possibility of also including a third degree murder charge.
August 27th, 2020 at 10:38 pm
Another service? preventing kidney stones on topamax But scrapping perks is also a business decision. At some point, some executive will demonstrate that a given perk’s cost exceeds its benefits. Paradoxically, as soon as a perk becomes established, it loses its motivating power and becomes a potential liability. Ex-Googlers tell us that the crackdown on 20% time began during the post-crisis recession, as the company’s revenues declined. This suggests that 20% time has long been viewed by management as just another expensive indulgence.
August 27th, 2020 at 10:38 pm
Looking for work cephalexin 500 mg side effects for dogs The Mainichi newspaper said Obuchi’s political fundingoversight body had spent about 3.6 million yen over five yearsfrom 2008 at a clothing shop run by her sister’s husband and adesign office run by her sister.
August 27th, 2020 at 10:43 pm
Looking for a job monoket
“I put her in the tub, and started filling it up. I went to go find my son so I could put him in the shower, saw the iPad, heard the little ping, an email from a friend,” Meer, 36 of Hartford, Conn., said on “Good Morning America.”
August 27th, 2020 at 10:44 pm
How much does the job pay? claritin prescription name The downturn in mining sales is not the company’s onlyresource-related headache. In January, Caterpillar said it waswriting off three-quarters of the money it paid for ERA afteruncovering “deliberate, multi-year, coordinated accountingmisconduct” at a subsidiary of the Chinese firm.
August 27th, 2020 at 10:44 pm
Remove card diovan prescription drug “This troubling shift in policy raises a number of questions about whether Facebook is improperly altering its privacy policy without proper user consent and, if the changes go into effect, the degree to which Facebook users will lose control over their personal information,” according to Markey’s letter.
August 27th, 2020 at 10:44 pm
Free medical insurance mifepristone misoprostol buy Einhorn said in a quarterly note to investors dated July 26 that investor sentiment toward the stock was “incredibly bearish” but that he expected the shares to recover. He also said Apple was in a “better competitive position” than Samsung.
August 27th, 2020 at 10:45 pm
Please wait viagra online europa Fey and Poehler’s understated tone also will be mimicked by the Oscars this year, as organizers brought on comedian and talk show host Ellen DeGeneres to lead the Academy Awards after “Family Guy” creator and provocative comedian Seth MacFarlane drew mixed reviews for his sometimes raunchy act in February.
August 27th, 2020 at 10:45 pm
I was born in Australia but grew up in England celebrex purchase canada As Simon Borrows, chief executive of British private equitygroup 3i, said: “Do the people that raise all the moneythen remain disciplined and spend it wisely, rather than rush toget the money out of the door?”
August 27th, 2020 at 10:45 pm
It’s serious 600 ibuprofen dosage Data showed consumer prices rose broadly in July and newclaims for jobless benefits fell to a near six-year low lastweek, factors which could draw the Fed closer toward trimmingits $85-billion monthly bond-buying program.
August 27th, 2020 at 10:46 pm
I stay at home and look after the children trental 400 mg Slaughter said that although the 22 have declared supportfor an unconditional bill to fund the government, they havesided with their own Republican leaders and the conservative TeaParty wing in repeatedly opposing Democratic efforts to bringsuch a Senate bill up for a House vote.
August 27th, 2020 at 10:47 pm
The United States bimatoprost prescription When Dr. King spoke of racism 50 years ago, the color lines were absolutely clear: they were marked by the back of the bus, by the whites-only water fountains and by the whole concept of separate but equal. Today our struggle is not where we sit on a bus. Racism today is not so overt. But in many ways it is more pernicious. It has been subtly institutionalized. It still inflicts harm, but it has been labeled something else.
August 27th, 2020 at 10:49 pm
Who do you work for? can tylenol get rid of period cramps But it will not be with any thanks to all the world’s countless mealy-mouthed, hypocritical, double talking, opportunistic politicians, who could not on their own, even escape from a simple paper bag, if their lives depended upon it.
August 27th, 2020 at 10:49 pm
I’ve come to collect a parcel allegra kuhn Nationalist aspirations now tend to be channelled into peaceful political activity, and a majority of Corsicans appear to be in favour of greater autonomy rather than outright independence from France.
August 27th, 2020 at 10:52 pm
A jiffy bag can you buy paxil online Real estate prices in China have soared, driven partly by a flood of government spending and bank lending in response to the 2008 global crisis. That is despite government curbs imposed on lending and purchases to cool housing costs.
August 27th, 2020 at 10:52 pm
Will I have to work on Saturdays? alesse 21 price canada Video editor Tom, also 54, said: “The house is totally flooded. It’s not really hit us yet. We can’t live in the house so we’ll have to get a hotel. In the long term we’ll have to move to rented accommodation. It could be six months before we can get back into the house.
August 27th, 2020 at 10:52 pm
Do you play any instruments? uk kamagra now Blackstone and Affinity officials were not immediatelyavailable to comment. ERA is the market leader in the realestate broking business in Singapore with more than 5,100 salesagents, a statement said.
August 27th, 2020 at 10:54 pm
Which university are you at? where to buy flagyl for cats The states with the highest rates of alcohol consumption also make it easier for consumers to purchase beer with relaxed restrictions. None of the 10 states with the highest beer consumption outlaw sales of beer at grocery stores or convenience stores. While many other states prohibit Sunday beer sales, all of the top-consuming states allow it.
August 27th, 2020 at 10:54 pm
prednisone steroids
August 27th, 2020 at 10:54 pm
How long are you planning to stay here? nolvadex pct amazon The former University of Colorado neuroscience graduate student has pleaded not guilty by reason of insanity. Defense lawyers said in recent court filings their client was “in the throes of a psychotic episode” when he went on the shooting spree.
August 27th, 2020 at 10:54 pm
I have my own business zofran ex “I think Joe has been consistent since we’ve had him here,” Cashman said. “The teams have changed, for instance, talent level, health, what he’s had to run out on a daily basis from year to year. The personnel has been different, but his effort and his efforts in pregame, in preparation for each series, how he runs major-league spring training as well as getting the 25 that are active competing on a daily basis, I think he’s been consistently tremendous at it.
August 27th, 2020 at 10:54 pm
I’ve lost my bank card buy tofranil It’s all a sign that the Pebble Beach Concours, the greatest classic car show on earth, is going plebian, although that’s a relative term in this rarified setting. Tickets to Sunday’s big show cost $225 in advance and $275 at the door. Some classic cars will fetch millions of dollars at pre-show auctions; Gooding & Co is estimating more than $3 million for a 1948 Alfa Romeo 6C 2500 Competizione roadster. Vintage California wines flow freely at the myriad parties and receptions leading up to Sunday’s show.
August 27th, 2020 at 10:55 pm
I’d like to cancel this standing order best place to buy crestor The Atlanta-based rapper, initially known as Tity Boi, was a member of the rap duo Playaz Circle before going solo. His 2012 debut album, “Based on a T.R.U. Story,” topped the Billboard charts. His new album, “B.O.A.T.S. II: Me Time,” is set to be released next month.
August 27th, 2020 at 10:56 pm
Where do you come from? abilify 5mg cost
The Greenpeace activists, ship’s crew, and two freelance journalists, have all been charged with piracy as part of an organized group — a charge that carries a sentence of 10 to 15 years under Russian law.
August 27th, 2020 at 10:58 pm
A pension scheme rogaine results on hairline Initially confined to Rakhine state, sectarian attacks have spread this year into Myanmar’s heartland, ravaging several other cities across the country. At the same time, a Buddhist-led campaign called “969″ has taken root nationwide. Its supporters urge Buddhists to shop only at Buddhist stores and avoid marrying, hiring or selling their homes or land to Muslims.
August 27th, 2020 at 11:00 pm
I’d like to withdraw $100, please tamoxifen cre jax “I suggested the need for the United States and Russia to work together to deal with this particular problem,” Obama recalled to Fox News in an interview that aired Monday. “It doesn’t solve the underlying Syrian conflict. But if we can solve this chemical weapons issue â which is a threat to us and the world â then it does potentially lay the groundwork for further discussions around how you can bring about a political settlement inside of Syria.”
August 27th, 2020 at 11:00 pm
A book of First Class stamps vytorin setia settlement The first beams, however, did not pass at the maximum speed, as the scientists set them for lower energy at first, soon to be steadily accelerated over the next few months
August 27th, 2020 at 11:00 pm
Pleased to meet you mercury drugstore cialis “My understanding is that the teacher, doing appropriate classroom management for middle school, said, ‘All right guys, settle down, that’s enough,’” Superintendent of Schools Dr. Mary P. Conway told ABCNews.com. “They did it one more time and the teacher said, ‘That’s enough. I don’t want to hear it again.’
August 27th, 2020 at 11:01 pm
Where are you from? cialis tadalafil buy online
Declaring the start of a “new model of economic development”, Mr Agon said the strategy was key to L’Oreal’s plans to double the number of consumers using its products to 2bn people worldwide.
August 27th, 2020 at 11:03 pm
What do you want to do when you’ve finished? can you take topamax for nerve pain Attracted to the glass towers of finance in London, New York and Singapore by the prospect of securing a full-time job and hefty wage, future “masters of the universe” often face 20-hour days in some of the most adrenaline-soaked offices on earth.
August 27th, 2020 at 11:03 pm
A few months where to buy tetracycline hydrochloride In contrast, the government of neighbouring Spain is facing corruption scandals, a shrinking economy, unemployment of more than 26 per cent and a â¬943bn (£793bn) debt equal to 92.2 per cent of the countryâs economic output.
August 27th, 2020 at 11:03 pm
I’ll text you later mechanism of action of tetracycline in rosacea He knows he did it on purpose, his family knows he did it on purpose and HER family and friends knows he did it on purpose. He’s a roided out freak who cornered that poor girl (fully clothed, with her purse and phone with her) in the bathroom.
August 27th, 2020 at 11:03 pm
Could I make an appointment to see ? mirapex bodybuilding
An attorney for former University of Miami pitching coach Lazaro Collazo, for example, claimed in court papers opposing a deposition filed in May in Miami-Dade County circuit court that MLB investigator Neil Boland and senior counsel Patrick J. Houlihan engaged in âintimidation, harassment, coercion, embarrassmentâ when they questioned Collazo about Bosch and Biogenesis. Collazo said the investigators came to his home and frightened his wife and two youngest children.
August 27th, 2020 at 11:05 pm
Could I make an appointment to see ? mebendazole cvs “Hey, did you know that Jamie just got the Red Poll Calf in Farmville and claimed some animal feed. Well, now you do and oh, by the way, did you see Bertha’s latest score in Lucky Slots?” Does anybody really need to know that their friends are playing some mindless game to wile away the hours at work? It’s basically just advertising in disguise, and can seriously clutter up your news feed. Definitely a feature that needs to be turned off.
August 27th, 2020 at 11:05 pm
we prefer to honor numerous other online web pages around the web, even if they aren�t linked to us, by linking to them. Beneath are some webpages worth checking out
August 27th, 2020 at 11:07 pm
How many days will it take for the cheque to clear? cipropol “One of the advantages of being a doctor is that it gives you a sense of perspective,” he says. “A baby with a cord around its neck is a crisis. People writing nasty things in the press is unpleasant, but it’s not the same thing.”
August 27th, 2020 at 11:07 pm
I’ve just started at side effects losartan potassium 25 mg Javier Caraballo, Panama’s top anti-drugs prosecutor, said the planes gave off a strong odor of gasoline, indicating that they had likely been used recently. So far, Panama has not found anything not on the Cubans’ list of ordnance, he added.
August 27th, 2020 at 11:07 pm
I’m sorry, she’s tenormin 25mg âNot to say that this game doesnât count, but with the distractions and everything in the regular season, I just felt that it could (take) away and not be a positive thing for me. So thatâs why weâre doing this now.â
August 27th, 2020 at 11:08 pm
Go travelling l arginine gnc uk But this past February, Bartoli arrived at the same crossroad that a number of great athletes and their parents-as-coaches often do. She and her father parted ways, and after some shopping around Bartoli wound up settling on former Wimbeldon champion and countrywoman Amelie Mauresmo. And indeed, she got fitter and more mobile.
August 27th, 2020 at 11:11 pm
Could I take your name and number, please? prilosec buy Since 1993, it has hosted more than 115 missions that resulted in more than 300 peer-reviewed studies. It is owned by the National Oceanic and Atmospheric Administration (NOAA) and operated by Florida International University (FIU).
August 27th, 2020 at 11:12 pm
I work for a publishers buy propecia finasteride australia âThis indicates 15 local authorities â just under half â have had no serious incidents. We accept that in some areas this may be the case, but we strongly recommend that other areas ensure they notify us.â
August 27th, 2020 at 11:12 pm
I wanted to live abroad l’oreal arginine shampoo reviews Since 2007, five Iranian nuclear scientists, as well as the nationâs ballistic missile program director, have been assassinated in attacks the regime routinely blamed on Israel. Typically, Israel has declined to comment on the assassinations, other than to convey off the record to reporters that it was not dismayed by such developments. But Yaakov Peri, former chief of Israelâs security agency, Shin Bet, and a current cabinet minister, told Israel Radio Ahmadiâs murder has the hallmarks of an âinternal dispute.â
August 27th, 2020 at 11:13 pm
I live in London generic rogaine foam for women Sage and team grew SCLC tumors from human cells in the lab and also tested the effects of the antidepressant medicine in mice that had been implanted with SCLC cells. In these tests the antidepressants — specifically imipramine — worked by activating certain receptors that triggered a death mechanism in the cells. This not only kills the cells, but also stops the cancer from developing immunity to the medicine.
August 27th, 2020 at 11:13 pm
i’m fine good work buy zyprexa online canada More than four years after Obama outlined his plan to haltthe housing market free fall in February 2009, he returns toPhoenix, where he will again talk about housing. The speech isanother stop in a summer tour in which he is highlightingaspects of the economy that have improved under his watch whilechiding political foes for obstructing faster progress.
August 27th, 2020 at 11:14 pm
Best Site good looking cipralex 10mg tablets
âI think that has been missing from the No campaign in particular. I feel that it has been all a bit managerial and we do need to be spikier, wittier and prepared to talk real time about what matters to people.â
August 27th, 2020 at 11:14 pm
Pleased to meet you tipo de viagra The deal represents the first big purchase of a Chinesecompany by a blue-chip U.S. buyer since Caterpillar Inc bought ERA Mining, a maker of underground mining equipment, in2012. Caterpillar later discovered an ERA subsidiary had engagedin accounting misconduct that inflated ERA Mining’s value.
August 27th, 2020 at 11:15 pm
When can you start? buy nexium on line Before the obvious grade-school insults begin to arrive from Minnesota saying that the name Packers is offensive too (very original,) let me say I know from personal experience that Mark Murphy is one of the finest people you will ever meet. A very stand-up individual and a great guy to run this unique franchise. Enough said.
August 27th, 2020 at 11:16 pm
Do you have any exams coming up? avanafil release date uk There are more significant changes inside, with upgraded plastics, a new dashboard design and a “Uconnect” touchscreen entertainment system with Bluetooth connectivity, voice recognition and optional sat-nav system.
August 27th, 2020 at 11:16 pm
Where are you from? rx-canadian.com Mrs Justice Eleanor King said she considered the restoration of his independence and the resumption of his relationship to be of the utmost importance and agreed with his carers that it should be protected and nurtured.
August 27th, 2020 at 11:21 pm
I’d like to send this parcel to mestinon timespan side effects Obama and other White House officials acknowledged that the FCC, as an independent agency, would ultimately shape the regulations
August 27th, 2020 at 11:22 pm
There’s a three month trial period tretinoin 0.05 Prosecutors said that Remy â whose father, Jerry Remy, is a former Red Sox second baseman and a broadcaster for the team since 1988 â viciously attacked Martel during a bloody rampage inside the coupleâs home Thursday night.
August 27th, 2020 at 11:22 pm
I’d like to send this letter by viagra in canada for sale But, at the margin, they said a scenario where Merkel formsa grand coalition with the Social Democrats, seen as more opento European integration and liability-sharing than she is, wouldbe supportive for periphery and hurtful for safe-haven Bunds.
August 27th, 2020 at 11:22 pm
Hello good day cheap purchase online prostate rx The recent decision by Standard and Poor’s to downgradeItaly’s sovereign rating to ‘BBB’ was not consistent with thecountry’s fundamentals, Visco said. (Reporting by Francesca Landini and Alessandra Prentice;Editing by Mark Potter)
August 27th, 2020 at 11:22 pm
How much will it cost to send this letter to ? buy maxidus canada
The pressure is building for the Redskins to change their name and the NFL has scheduled a meeting next month to meet with members of the Oneida Indian Nation, who consider the nickname offensive to Native Americans.
August 27th, 2020 at 11:23 pm
I’d like to tell you about a change of address proscar et grossesse Egypt also last month hosted an experts’ meeting to study the impact of the dam on Egypt and Sudan, the two downstream Nile states. The foreign ministry said Cairo’s proposed meeting was going to discuss that study, but gave no further details.
August 27th, 2020 at 11:23 pm
We used to work together viagra patent expiration date uk Sheriff’s spokeswoman Cheryl Church says the trampoline was properly assembled, was anchored to the ground and had a safety net. She says it was a tragic, freak accident that has affected the entire county.
August 27th, 2020 at 11:24 pm
What’s the current interest rate for personal loans? doxycycline 100mg cap âItâs vitally important that countries implement the measures contained in the [World Health Organisationâs] Framework Convention on Tobacco Control and resist pressures from the tobacco industry to weaken or undermine this process.â
August 27th, 2020 at 11:24 pm
I like watching football buy cheap rogaine uk Police arrested 57-year-old Marcus Wesson, who emerged from the residence with blood on his clothes. Neighbors’ accounts led police to believe that Wesson controlled his family in a cult-like manner, and that he possibly had fathered several of the deceased children with his own daughters and nieces.
August 27th, 2020 at 11:29 pm
Get a job can i buy metronidazole online uk Bae’s sister, Terri Chung, of Edmonds, said Sunday the family recently learned that he has been transferred from the labor camp to a hospital. Her brother suffers from diabetes, an enlarged heart, liver problems and back pain, she said.
August 27th, 2020 at 11:31 pm
It’s OK how to get a discount on nexium Americans for Prosperity, another conservative group, has spent millions on television ads in selected states that show mothers and other women worrying about whether their healthcare will suffer with the government “in the middle of things.”
August 27th, 2020 at 11:31 pm
I’m a trainee magnet-mri.org However, please note - if you block/delete all cookies, some features of our websites, such as remembering your login details, or the site branding for your local newspaper may not function as a result.
August 27th, 2020 at 11:31 pm
Who do you work for? can i buy viagra in tijuana NEW YORK, Aug 23 (Reuters) - U.S. stock index futures werelittle changed on Friday, a day after the Nasdaq stock exchangesuffered a historic trading halt of roughly three hours as aresult of technical problems.
August 27th, 2020 at 11:31 pm
Can I use your phone? buy accutane online New Yorkâs inequality is extreme. Manhattan is the most unequal big county in the U.S., and the New York area is the countryâs seventh most unequal metropolitan area. The Bronx and Brooklyn are more unequal than 90% of Americaâs more than 3,000 counties.
August 27th, 2020 at 11:31 pm
I’ve only just arrived comprar cialis 5mg em portugal “I have not been provided any information from CMS onwhether the hub would operate” in the event of a governmentshutdown, said Rocky King, executive director of Cover Oregon,that state’s Obamacare marketplace.
August 27th, 2020 at 11:31 pm
I like watching football cefadroxil 500 mg alcohol The civil engineering business made a loss,despite some revenue growth, because of the project writedowns.
August 27th, 2020 at 11:32 pm
How do you do? cost of risperdal consta uk Nutrition researchers at Griffith University’s Health Institute added electrolytes to two commercial beers â one regular strength and light beer â before giving it to participants who had just exercised.
August 27th, 2020 at 11:33 pm
I work here levothyroxine online You can see the QWERTY keyboard in these images, which looks like the laser cut 5-row keyboard that featured on the Droid 4. The phone is said to have wireless charging and NFC as well as a design that is not only water and dust resistant but also shockproof. The Verizon 4G LTE branding can also be seen on the reverse and the display looks to be anything between 4.3 and 4.5-inches.
August 27th, 2020 at 11:33 pm
I’ll call back later longinexx in the uk Denis Sinyakov, a former Reuters photographer, was working on a freelance contract for Greenpeace and on assignment for a Russian news site when the group’s Arctic Sunrise icebreaker was boarded by Russian forces last month.
August 27th, 2020 at 11:35 pm
Where do you study? neogyn australia
The procedure to become a gestational carrier entails collecting fertilized eggs from the biological parents via in vitro fertilization, then taking the resulting embryo and implanting it in the carrierâs own uterus, reports ABC News. It was a success and Kozisek was able to give birth to twin granddaughters Hallee and Hadlee. Kozisek had previously carried the twinsâ older sister, Harper, in June 2011.
August 27th, 2020 at 11:39 pm
I work here target nexium price Two witnesses backed Sikoutris’ claims, while additional reports confirmed that a man and a female companion sitting in Row 5 of Section 42 were removed from Fenway Park by stadium security after he snatched Alex Avilaâs two-run, sixth-inning shot from a womanâs hands and threw the ball back onto the field.
August 27th, 2020 at 11:39 pm
I’ve got a full-time job where to buy diflucan Two of the four prime spectrum blocks on offer match with Verizon’s frequency, while the other two match with that of AT&T Inc. AT&T declined to comment on whether it was interested in the Canadian market.
August 27th, 2020 at 11:39 pm
I was born in Australia but grew up in England prilosec price comparison Rodriguez was originally supposed to have a sim game at the club’s minor-league complex about a mile away, but the grounds there were too wet following Wednesday night rain. The club announced later on Thursday that A-Rod would play for Double-A Trenton on Friday and Saturday.
August 27th, 2020 at 11:40 pm
I saw your advert in the paper glucophage 1 g Last night, Ask.fm released a statement describing the latest death as a “true tragedy” and said it would co-operate with the Leicestershire Police investigation. But in May, Mark Terebin, 28, claimed that in 90 per cent of cyber-bullying cases, teenagers actually posted the nasty comments themselves as a means to get attention. In a statement given to an Irish broadcaster, following the suicide of 13-year-old Erin Gallagher from County Donegal, last October, he appeared to suggest that British children were to blame for the recent tragedies.
August 27th, 2020 at 11:40 pm
I’ll send you a text clindamycin 300 mg dosage for acne The Euro STOXX 50 gained 1.3 percent, rising to2,694.84, jumping above the June 19 close at 2,684 just beforethe Fed confirmed it was looking to slow asset purchases by theend of the year, sending shares sharply lower the following day.
August 27th, 2020 at 11:40 pm
i’m fine good work the physician has ordered 1.0g of tetracycline to be Klinsmann was irate Wednesday after the referee failed to issue cards on a series of hard fouls against the Americans. He could be seen yelling and gesturing angrily in the direction of the referee, and was told to leave the field after he slammed a ball into the ground.
August 27th, 2020 at 11:40 pm
In a meeting erythromycin ees 400 mg tablets The Internet and social media in Kenya, which played a central role in this year’s elections by allowing Kenyans to question candidates, took on a new function Tuesdayâspreading messages of peace to avert new bloodshed.
August 27th, 2020 at 11:41 pm
Could I make an appointment to see ? extreme fit 180 garcinia cambogia reviews The animalâs response to stress gets interpreted as hardship by the witness, but âstress can also be caused by virtue of the fact that theyâre testifying falsely,â said Tohomâs lawyer, Steven Levin.
August 27th, 2020 at 11:41 pm
When can you start? chi usa cipralex “Their lineup is so deep,” admired Zack Greinke, the Dodgers’ Game 1 starter. “They have injuries, and then they bring up someone and it’s like they don’t miss anything even if it’s a real important player. They don’t really give up any at-bats, so it’s always a grind. Even when they bring the young guys up, it’s like they make adjustments faster than other teams.
August 27th, 2020 at 11:42 pm
I can’t hear you very well consultorio.unimeds.com.br/adm/login/expirou.aspx “The United States must make it clear to India’s topleadership that barriers to free and open trade between Indiaand the United States must be addressed if our close economicand diplomatic relationship is to continue to grow,” StephenEzell, senior analyst with the Information Technology andInnovation Foundation, said in a blog about Biden’s trip. (Reporting by Doug Palmer; editing by Christopher Wilson)
August 27th, 2020 at 11:44 pm
I’d like to cancel this standing order aspirin 81 mg walmart canada
FRANKFURT, Sept 25 (Reuters) - Activist investor Cevian hasraised its stake in ThyssenKrupp to 5.2 percent andsaid it could buy more, in a move that was welcomed by theGerman steelmaker’s CEO who is struggling to push the firm intonew higher-margin businesses.
August 27th, 2020 at 11:47 pm
Could I have a statement, please? where can i get clomid in south africa Russia has been Assad’s most powerful backer during theconflict that has killed more than 100,000 people since 2011,delivering weapons and - with China - blocking Western effortsto use the Security Council’s clout to pressure his government.
August 27th, 2020 at 11:47 pm
The National Gallery naproxen prescription only uk Investigators continue to scour the area in the town of Lac-Megantic in Quebec, with as many as 50 people still reported missing by family and friends. Some of the bodies that have been recovered are so badly burned that families are being asked to find DNA samples of their loved ones to help identify them.
August 27th, 2020 at 11:48 pm
I’m at Liverpool University where can i buy clarithromycin 500mg Line rental makes up most of the cost of some broadband services. TalkTalk’s cheapest broadband service, for example, costs £6.50 a month but as much as £14.95 extra in line rental.
August 27th, 2020 at 11:49 pm
I’m on holiday generic seroquel problems From Audrey Hepburn’s little black dress in “Breakfast at Tiffany’s” to Alicia Silverstone’s preppy-chic knee-high socks and plaid miniskirts in “Clueless,” fashion has long had a memorable place in film.
August 27th, 2020 at 11:49 pm
I went to can you buy viagra at pharmacy âIt was a fast half, but I thought it was a two-horse race,â said winning driver Yannick Gingras, the Big Mâs leading driver. âI got the jump, making the lead first, and figured Iâd take some of Johnâs (Campbell, Nuncioâs driver) power away by taking it to him a little bit, and my horse responded. He won very, very easy.â
August 27th, 2020 at 11:49 pm
A Second Class stamp buy fluoxetine no prescription Aston Villa, without their key striker Christian Benteke through injury, bring back Brad Guzan, Ciaran Clark, Antonio Luna, Fabian Delph and Andreas Weimann after their midweek Capital One Cup loss to Tottenham. Gabriel Agbonlahor is missing.
August 27th, 2020 at 11:50 pm
What are the hours of work? best drugs to get off opiates And Archie Manning, when the first weekend of the season is finally over, knowing that on the second Sunday Peyton and Eli will be playing against each other at MetLife Stadium â and maybe for the last time â is able to step back and say, âOlivia and I still pinch ourselves, because we do both understand this isnât normal.â
August 27th, 2020 at 11:51 pm
What are the hours of work? cialis 2.5 mg review What they won’t find quite so appealing is the odd cabin layout - the second row has only two individual seats, with a gaping space in the middle. That means access to the rear row is easy, but means that anyone with three kids will have to relegate one to the back seat.
August 27th, 2020 at 11:51 pm
I like watching football levitra 20mg preis Her words are not to be taken for granted. They are urgent on most of the planet. Tens of millions of girls are out of school, about half of them in sub-Saharan Africa. A third of women aged 20 to 24 years old in developing nations were married as children, most of them given to an older man as property.
August 27th, 2020 at 11:53 pm
Will I get travelling expenses? arimidex estrogen starvation Morgan grew up hoping to join the military, but failed to complete National Guard boot camp during Desert Storm
August 27th, 2020 at 11:53 pm
Do you know the address? getting off of zocor Although it is not quoted in London and specialises in making products such as high-pressure vacuum pumps which are unfamiliar to the general public, the deal will nevertheless be closely-watched in Britain.
August 27th, 2020 at 11:55 pm
I really like swimming xenical orlistat 120 mg adalah Meanwhile, Forbes.com reported that a 36-year-old soldierliving in Spain’s Canary Islands, Jose Rodriguez, has alreadyuncovered a security vulnerability affecting iOS 7, which Applebegan distributing to existing iPhone and iPad customers onWednesday.
August 27th, 2020 at 11:55 pm
We went to university together mangal pharmacy Unfortunately three years later, our financial system is not much more resilient. Much of the law has yet to be fully implemented, due to unceasing lobbying by the banking industry. Fortunately, last week brought several signs of progress for those who want a stable and sustainable banking system that serves all Americans.
August 27th, 2020 at 11:58 pm
I was born in Australia but grew up in England where to buy ibuprofen in japan âTheyâre in our clubhouse every day,â said an agitated Collins. âTheyâre there on the road. Iâd like to get to the point where weâre not worrying about all the extracurricular stuff.â
August 27th, 2020 at 11:58 pm
What’s the exchange rate for euros? duphaston et envie de grossesse Saudi Arabia produced record high volumes of crude in Augustas it boosted output for the second time in two years to cushionthe global oil market from supply disruptions. Naimi’s commentscome after producer group OPEC this week sought to reassureconsumers there is sufficient supply to cover a plunge inLibya’s output.
August 27th, 2020 at 11:59 pm
Do you have any exams coming up? is lasix a potassium sparing diuretic The Browns asked media members not to report Miller’s name until his family could be contacted, raising fears he was hurt more severely. And, as Miller was being treated, the team also requested for cameras be turned off to protect his privacy.
August 27th, 2020 at 11:59 pm
I can’t hear you very well cheapest pharmacy for synthroid
Some exchanges were hobbled even by much lighter traffic than New York’s. Kentucky’s Kynect exchange was “swamped” with 60,000 visitors, Gov. Steve Beshar said, with the “crush of hits” revealing a glitch that kept the exchange from filing applications for several hours.
August 27th, 2020 at 11:59 pm
Very interesting tale walmart pharmacy propecia price The U.S. Embassy in Kampala this week said it continues to assess reports that a “Westgate-style attack may soon occur in Kampala.” The embassy said it was sharing information with Ugandan authorities and told U.S. citizens “to exercise vigilance and to avoid public venues that attract large crowds.”
August 28th, 2020 at 12:00 am
Insert your card best price prilosec Leave aside the debate whether global warming intensifies the weather of the age. These storms ranked among the weakest of their kind. But local human folly provided more than enough cause for calamity.
August 28th, 2020 at 12:00 am
Could you please repeat that? macrobid price us Geologists say it is part of the continuing process of continental drift, or the drift of land mass across the oceans that brought the Indian sub-continent to collide with Eurasia and created the fault-lines, some of which run through the Makran coast.
August 28th, 2020 at 12:00 am
When do you want me to start? diflucan over the counter canada “I guess for the most part I feel quite comfortable on most of the holes,” said Garcia, who hit 83.33 percent of his fairways, up nearly 20 points from his season average. “I guess if you’re playing well early on, the first couple of times you play, you kind of seem to like it a little bit better.”
August 28th, 2020 at 12:01 am
Have you seen any good films recently? buy finasteride walmart The Yankees Entertainment & Sports Network should benefit greatly, in terms of ratings, which have been subpar this season. YES has a chance to hit paydirt in the home finale. What looked to be a meaningless game should become another iconic moment in Yankees history. The prospect of seeing two of the storied franchiseâs most dependable, and revered, arms simultaneously bidding adieu to the Bronx should attract a major influx of eyeballs.
August 28th, 2020 at 12:01 am
I’d like to speak to someone about a mortgage half inderal la 80 mg for anxiety “It seems like an improvement in the euro zone economic datahas stalled. In addition, now that Germany’s election is over,the market could dust off the issues that had fallen out offocus, such as further aid to Greece,” said Masafumi Yamamoto,forex strategist at Praevidentia Strategy.
August 28th, 2020 at 12:01 am
I read a lot humanwellpharma.com The 27-year-old was arrested May 23 after allegedly rolling a joint and smoking it in the lobby of her New York City apartment building. Police were called, went up to her place and, they said, saw a bong on the kitchen counter.
August 28th, 2020 at 12:03 am
I saw your advert in the paper prostenal forte uk We’re hoping the Suzuki i-V4 makes it to production relatively unchanged because we rather like the styling, particularly the colour-coded alloy wheel inserts and the sweeping lines. It’s a bit like a taller, stubbier Land Rover Evoque from certain angles, which is no bad thing for a car likely to cost a whole lot less.
August 28th, 2020 at 12:03 am
Could you transfer $1000 from my current account to my deposit account? testcore pro 2017
Over the past couple of years Woodford has continued to provide strong returns to his investors. The High Income fund has delivered 42pc and his Income fund has returned 41pc. By comparison, the average UK income fund has returned 35pc.
August 28th, 2020 at 12:03 am
Until August viagra rezeptfrei osterreich The JLA Speakers Bureau, the UK’s biggest corporate entertainment company, is due to post record annual revenues next month – up 17pc on the previous year – after corporate clients between them booked entertainers for 2,100 events, including about 300 awards ceremonies, over the last year.
August 28th, 2020 at 12:03 am
Your account’s overdrawn super viagra “Any invasion of privacy at the hands of our trusted health personnel or extended care team of training fellows is unacceptable and not indicative of the Patients’ First culture of Northwestern Memorial Hospital, which has zero tolerance for exploitation of private health information, including photography,” the hospital said in a statement.
August 28th, 2020 at 12:04 am
We need someone with experience discharge with tamoxifen Central time (0930GMT), the woman and her husband disembarked and drove away intheir own car, a Carnival spokeswoman said at a brief pressconference in Galveston
August 28th, 2020 at 12:07 am
I’m not sure nizagara 100 reviews
Those sources point to a confluence of events which will see the Chancellor push the button on the share sale, despite Danny Alexander, chief secretary to the Treasury, insisting there is no fixed timetable for a Lloyds sell-off.
August 28th, 2020 at 12:08 am
A pension scheme bimatoprost ophthalmic solution uk An Egyptian boy walks near a defaced picture of former Egyptian President Hosni Mubarak with Arabic words reading, ‘’Corrupt and deposed'’ and a poster of presidential candidate and former leader of the Muslim Brotherhood Abdel Moneim Abol Fotouh (L) in Cairo May 24, 2012.
August 28th, 2020 at 12:08 am
Please wait buy estradiol transdermal patch Alex Rodriguez (r.) shakes hands with Don Hooton after a news conference in 2009 at George Steinbrenner Field in Tampa. Hooton started the Taylor Hooton foundation after his son Taylor died of suspected steroid use.
August 28th, 2020 at 12:09 am
A financial advisor buy topiramate uk The empathy and yawning link has previously been studied in chimpanzees, baboons and other primates. Human and animal studies have shown that when two subjects share a close social connection, contagious yawning is more frequent.
August 28th, 2020 at 12:09 am
A book of First Class stamps lowest price plavix The country has some way to go however, to address the problems that have left tens of thousands of Britons at best disenchanted with their Spanish investments and at worst fighting through the courts to win back losses through property scams.
August 28th, 2020 at 12:10 am
real beauty page generic viagra vega sildenafil citrate âAcross many of the worldâs poorest countries, armed conflict continues to destroy not just school infrastructure, but also the hopes and ambitions of a whole generation of children,â UNESCOâs Director-General Irina Bokova said.
August 28th, 2020 at 12:10 am
A few months diva viagra pour femme But it comes less than a week after the Obama administrationoverturned an ITC decision from June that would have banned thesales of some older-model Apple iPhones and iPads in the UnitedStates for violating Samsung patents.
August 28th, 2020 at 12:11 am
I quite like cooking buy kamagra in canada Quick singles to rotate the strike and disrupt the bowler? Nothing so old-fashioned, thank you. Just fling the bat and see how many boundaries you can hit. Hence the astonishing statistic that England, out of their 194 runs off the bat, scored 152 in fours. No England batsman scored more than four singles.
August 28th, 2020 at 12:11 am
Best Site good looking permethrin cream 5 (also known as elimite) “I’m heading in to be non-essential,” said one Environmental Protection Agency worker on the metro transit system on Tuesday as she joined many others going to work just to cancel meetings, lock up files and set out-of-office messages on email and voice mail.
August 28th, 2020 at 12:12 am
Hold the line, please lexapro 20 mg online The combined company will have the financial resources,scale and spectrum to better compete with other major nationalproviders for customers interested in low-cost prepaid service,the companies said.
August 28th, 2020 at 12:16 am
This site is crazy chances of miscarriage after taking clomid The company, which also acquired certain bread brands frombankrupt Hostess Brands, forecast 2013 profit of 92-98 cents pershare. Analysts on average had expected a profit of 97 cents pershare, according to Thomson Reuters I/B/E/S.
chances of miscarriage after taking clomid The company, which also acquired certain bread brands frombankrupt Hostess Brands, forecast 2013 profit of 92-98 cents pershare. Analysts on average had expected a profit of 97 cents pershare, according to Thomson Reuters I/B/E/S.
August 28th, 2020 at 12:16 am
Yes, I play the guitar sildigra uk
“Cloudy 2″ has now earned $60.6 million at domestic theaterssince its release a week ago. The movie features the voices ofBill Hader and Anna Faris as characters in a world where foodhas come to life as food/animal hybrids called “foodimals.”
August 28th, 2020 at 12:17 am
How would you like the money? lamisil cream cost india âThe one on Crawford, I kind of felt in between on it, I wasnât sure I could get it clean on the straight backhand and get it in the air,â Murphy said. âOnce I left my feet it hit off my glove. The one with Ellis, it hit off the tip of my glove.â
August 28th, 2020 at 12:17 am
No, I’m not particularly sporty invite health The global alternatives investment firm hired Shailen Modias chief operating officer. Modi had previously worked withFauchier Partners, a fund of hedge funds where he was a partnerand CFO/COO until June 2012.
August 28th, 2020 at 12:17 am
What’s the last date I can post this to to arrive in time for Christmas? orlistat capsules price india The review found that people who had migraines were more likely to have changes in their brains than were people who didn’t have migraines. Those who had migraines with auras appeared to be more likely to have these changes than those who had migraines with no auras, but the association wasn’t found to be statistically significant, according to Ashina.
August 28th, 2020 at 12:19 am
How do I get an outside line? dosage of cefixime In fact, the administration is facing a nearly impossible diplomatic dilemma â how to balance support for the democratic process in Egypt, on the one hand, versus our interest in maintaining a close relationship with the military, on the other. The US has to try to protect both of these interests â thus the sheer degree of difficulty in this high wire act.
August 28th, 2020 at 12:19 am
I’ve got a very weak signal flagyl online purchase The prospect of the Fed buying fewer bonds by the end of theyear has made investors rethink some of the trades that werebuilt around the lower rates and excess liquidity that resultedfrom the program.
August 28th, 2020 at 12:19 am
It’s OK elavil 50 mg NEW YORK, July 12 (Reuters) - U.S. stocks were set to openlittle changed on Friday after closing at fresh record highs aday earlier, as rosy results from JPMorgan and Wells Fargo wereoffset by a profit warning from United Parcel Service.
August 28th, 2020 at 12:19 am
Where did you go to university? much does paxil cost canada And all the while, the useless, unspendable money keeps multiplying. The numbers on Walt Jr.âs cancer fighting charity website grow bigger. The stacks in the storage space grow higher. At this point, they can barely give the stuff away. When Walt tries to pay for a birthday breakfast, the waitress insists itâs free. Jesse tosses wads of it from his car and a good Samaritan reports it to the cops. Skyler hands a customer a five instead of a one and he demands the right change. Itâs the worst con ever, a perfect representation of how ultimately bad these guys have turned out at being crooks. They canât even scam a man into taking more than heâs owed.
August 28th, 2020 at 12:19 am
Hold the line, please nexium 20 mg 28 tablet fiyat�nexium 40 mg from canada The agency eavesdropped on civil rights leaders Martin Luther King and Whitney Young as well as boxing champion Muhammad Ali, New York Times journalist Tom Wicker and Washington Post columnist Art Buchwald.
August 28th, 2020 at 12:20 am
Hold the line, please sirtfood diet amazon The financial holding company said that its wholly-ownedsubsidiary, PlainsCapital Bank, has entered into an agreementwith the Federal Deposit Insurance Corp (FDIC) to buyTexas-based First National Bank. The transaction is expected tobe immediately accretive to PlainsCapital’s earnings.
August 28th, 2020 at 12:20 am
What do you do for a living? can u get zithromax over the counter “When I first started Muay Thai I wanted to lose weight but the dedication was not there,” she said. “And then slowly, slowly I realised this thing has to be consistent, there’s got to be discipline and a certain number of hours or days.
August 28th, 2020 at 12:22 am
Your account’s overdrawn buy cheap premarin Simon McKay, lawyer for the family, is keen to play down the wider implications of his case. He says the levels of negligence revealed in the Red Cap’s death in 2003 were so exceptional that it is almost a special case.
August 28th, 2020 at 12:22 am
I’m only getting an answering machine vente viagra au luxembourg In some ways, the chances of a slow or uncertain approvalprocess might argue for doing a little now, just to take thedrama off of the table. The problem with that is that marketsmay react so severely to the taper, in the U.S. and elsewhere,as to force the Fed to somehow hose investors down.
August 28th, 2020 at 12:25 am
What sort of music do you like? there generic erythromycin The shortfall in funds could curb Sharp’s efforts to turnaround its operations which, along with fellow Japanese consumerelectronics companies such as Panasonic Corp andToshiba Corp, have suffered from a slump in TV sales asforeign rivals encroached on their market.
August 28th, 2020 at 12:26 am
In a meeting albuterol sulfate 2mg/5ml syrup dosage Researchers from the Royal College of Surgeons in Ireland (RCSI) and Dublin’s Mater Hospital traced 212 people from different schools in north Dublin who had been interviewed when they were aged between 12 and 15, and re-interviewed them when they were aged between 19 and 24.
August 28th, 2020 at 12:26 am
Where do you live? ogoplex canada Who’s that? In mid-December, Jewish reggae star Matisyahu has sheared his trademark beard - and announced his rebirth as a non-Chassidic reggae star. ‘At the break of day I look for you at sunrise When the tide comes in I lose my disguise,’ he tweeted.
August 28th, 2020 at 12:26 am
Have you read any good books lately? over the counter viagra alternatives uk In May 2012, the United States suspended Argentina from theU.S. Generalized System of Preferences program, which waivesimport duties on certain goods from developing countries, afterthe South American nation failed to pay about $300 million incompensation awards in disputes involving Azurix and Blue RidgeInvestments. It was the first time a country had been suspendedfrom the program for failing to pay an arbitration award.
August 28th, 2020 at 12:26 am
Is this a temporary or permanent position? diamox prescription nhs In 2009, Jeff Blackburn, Amazonâs senior vice president for business development, ominously informed the Quidsi co-founders over an introductory lunch that the e-commerce giant was getting ready to invest in the category and that the startup should think seriously about selling to Amazon. According to conversations with insiders at both companies, Lore and Bharara replied that they wanted to remain private and build an independent company. Blackburn told the Quidsi founders that they should call him if they ever reconsidered.
August 28th, 2020 at 12:26 am
magic story very thanks alesse birth control price walmart
Shaikh - who had survived an earlier assassination attempt near his home in Karachi about a year ago - used to change his routes several times while travelling around one of Pakistan’s most violent cities.
August 28th, 2020 at 12:26 am
The United States crestor 20 mg price india
The company had priced its initial public offering at thetop end of the range at 27.50 pesos per share, and the sharesrose as high as 30.50 pesos in the first seconds of trading. Theshare sale netted the company more than $1 billion.
August 28th, 2020 at 12:27 am
The United States acheter viagra avec ordonnance “The investigations are progressing well, and we are optimistic some people will be prosecuted soon,” Kenya’s Inspector General of police David Kimaiyo told Reuters. He declined to give more details about the case.
August 28th, 2020 at 12:27 am
I’d like to pay this in, please pillsfind.com coupon Berlusconi’s conviction for tax fraud has shaken the stability of the left-right coalition, with the former prime minister’s People of Freedom (PDL) party demanding guarantees for his political future.
August 28th, 2020 at 12:27 am
How do you know each other? amoxicillin online uk Falkowski, now president of Drug Abuse Dialogues, an educational organization on drug and alcohol abuse in Minnesota, has heard stories of desperate addicts trying to distill fruit pilfered from the cafeteria into alcohol. At a treatment center where Falkowski worked in the 1970s, workers found drug syringes hidden in a clothes dryer.
August 28th, 2020 at 12:27 am
What do you want to do when you’ve finished? how to order generic valtrex Weeks of organizing crested with a nationwide general strike known as “8/8/88,” a date chosen for its numerological power. Thousands of people marched on the streets of Rangoon, the capital at the time, and in cities and towns around the country.
August 28th, 2020 at 12:29 am
What’s your number? revatio delivrance “I am glad you acknowledge prime minister Rahul Gandhi, but that is a question you should put to him,” Chidambaram said, when asked if he would serve again in a government led by the party’s heir apparent if Congress wins a third straight term in office. “The time has come for the torch to be passed on to a new and younger generation.”
August 28th, 2020 at 12:29 am
Jonny was here bula do medicamento flagyl 250 mg Business confidence in Britain rose 4.1 points on 2012, to62.55 out of 100, ahead of all the euro zone countries surveyed,including France, Portugal, Spain and Germany, according to thepoll of more than 11,000 enterprises across 17 countries.
August 28th, 2020 at 12:29 am
I’d like to transfer some money to this account where to buy tetracycline for cats Goff just missed his third straight 400-yard game to begin his career. He finished 31 for 53 passing but also threw an interception in the first quarter to put the Bears in a hole they could never escape.
August 28th, 2020 at 12:29 am
Please call back later cabergoline for sale uk He performed with jazz giants Charles Mingus, Betty Carter, Jackie McLean, Joe Henderson, Kenny Dorham, McCoy Tyner, Herbie Hancock, Wayne Shorter, Ray Bryant, Stanley Turrentine, Albert Ayler, Cecil Taylor, and Ornette Coleman, and then turned around as a leader and helped bring up a whole new generation.
August 28th, 2020 at 12:32 am
What’s the current interest rate for personal loans? erythromycin ophthalmic ointment cvs Once again, the Yankees sent Nova out to the mound in a critical start asking for just a solid outing. And once again, the Yankees got more than that. Much more, in fact, as Nova had arguably the best start of his Yankee career in a 2-0 win over the Baltimore Orioles. He was dazzling from start to finish, going the distance for the complete-game shutout — his first in a big-league uniform.
August 28th, 2020 at 12:34 am
acyclovir 5306
August 28th, 2020 at 12:35 am
I saw your advert in the paper corega krema cena Folks used to dream about Valdespinâs offensive potential, especially after heâd slug a dramatic pinch-hit homer. Of course, the excitement faded when he struggled when given a chance. Or threw a tantrum. Or butted heads with, well, everyone.
August 28th, 2020 at 12:36 am
About a year how do i get a viagra prescription Fund managers who were optimistic about Twitter’s financialprospects shrugged off its latest $65 million quarterly loss asstandard for startups chasing growth, pointing instead torevenue growth that more than doubled.
August 28th, 2020 at 12:36 am
We were at school together 10 off rogaine foam coupon Another possible explanation for the shift in the Beveridge curve is the expansion of unemployment insurance benefits, such as the 2008 extension of unemployment compensation. More generous benefits might encourage unemployed workers to slow their job searches, leading to more unemployment for a given number of vacancies. However, unemployment insurance benefits have been reduced substantially over the past two years, suggesting that the expansion of unemployment benefits is not a main factor behind the shift in the Beveridge curve.
August 28th, 2020 at 12:36 am
Where do you live? lithium carbonate buy uk While Oracle had already offered SaaS (software-as-a-service) applications, database-as-a-service and other products, it announced 10 additional cloud services at the OpenWorld conference in San Francisco on Tuesday.
August 28th, 2020 at 12:36 am
Where do you live? generic accutane reviews
“I want the government to understand that they are giving the wrong message to our youth, because our youth are understanding now that their blood has no worth and they are giving the wrong message to the other side, that they should go ahead and kill because it gives them power.”
August 28th, 2020 at 12:36 am
Do you know the number for ? cheapest genuine viagra uk âI think the rivalry is a good thing for New York,â Dolan said. âSo, from that point of view, itâs enjoyable. But, as far as how the teams will do, Iâm not going to make any prediction here. This is about the All-Star Game. My hope is that both teams will have a lot of players at the All-Star Game. That would be great.
August 28th, 2020 at 12:36 am
Directory enquiries generic dulcolax “The Daily Show” decided to have a little fun with what host John Oliver referred to at one point as the verbal “karma sutra” of State Department spokeswoman Jen Psaki and White House press secretary Jay Carney after more than two weeks of indirect answers to questions about whether former Egyptian President Mohamed Morsi’s ouster was the result of a military coup.
August 28th, 2020 at 12:36 am
Would you like to leave a message? comprar pariet desconto According to the researchers, this study supports the view that young people become concerned about their sexual orientation from a young age
August 28th, 2020 at 12:37 am
No, I’m not particularly sporty cialis tabs for sale Muslim community leaders raised more than $400,000 from around the world in less than three weeks to help rebuild the mosque in Joplin, the only Muslim house of worship within a 50-mile radius, according to a website posting at the time. Money is still being raised for the project.
August 28th, 2020 at 12:38 am
Stolen credit card adhd strattera wiki
You also make a great point about the final twist. I’m excited to see a season where there’s a little more internal drama and a little less bombast. And honestly, Saul (potentially) turning on Carrie is in many ways a more interesting plot point than, say, the vice president’s pacemaker being hacked.
August 28th, 2020 at 12:38 am
Could you send me an application form? viagra online bestellen ohne rezept paypal This stallion has an intriguing history. Originally a gift from Muley Ismael, King of Morocco, to Louis XIV of France, it was bought by Henry Curwen of Workington Hall in Cumberland through the offices of Count Byram, Louis’s illegitimate son and Master of the Horse.
August 28th, 2020 at 12:39 am
Could you ask her to call me? canadian valtrex
Former South African leader Nelson Mandela remains in critical but stable condition in hospital, though “medical interventions” are required because his health sometimes becomes unstable, the South African government said Saturday.
August 28th, 2020 at 12:39 am
Where do you study? nexium capsule dosage “Then we do another layer, and another, and so on, building up,” said Shear. “It’s very simple. We’re basically making pictures and stacking them up into 3-D structures, but with incredible control. Think about the thickness of a hair on your head, and take 1 percent of that, and then take about a quarter of that. That’s about the size of our laser when it’s brought to its smallest point.”
August 28th, 2020 at 12:41 am
Sorry, you must have the wrong number canadian pharmacy viagra + cialis spam
Craig later served as Sen. Ted Kennedyâs senior adviser on defense, foreign policy and national security issues from 1984-1988, and represented Kennedy in 1991 in connection with the rape trial of his nephew, William Kennedy Smith.
August 28th, 2020 at 12:43 am
Where do you study? dostinex tablets uses Martinez has started 39 consecutive games for the Cornhuskers and will leave the school with several offensive records. While he will go down as one of the best players ever at the powerhouse program, he doesn’t seem too concerned with his legacy headed into his final year.
August 28th, 2020 at 12:43 am
I’m interested in this position inexpensive viagra online
Asked whether the central bank might cut interest ratesagain in coming months, Hamam replied: “Of course, yes, but wehave to look at that. We have to watch inflation. Inflation isonly one factor. We have look at more than one factor.”
August 28th, 2020 at 12:44 am
Is it convenient to talk at the moment? nexium mups 40 mg precio mexico âJoe (Johnson) will play some minutes at small forward,â King said, adding that the Nets have the versatility to go with a small lineup. âStarting with the interview with (Kidd) and how he envisioned our players, moving guys in different positions.â
August 28th, 2020 at 12:45 am
We’d like to invite you for an interview can you buy prozac online So the conduct that is promulgated within the systems, both the entity itself and society-wide, is a critically important governor of operations, yet it’s one that has been largely thrown in the wastebin for the last 30 years. And we are reaping the results.
August 28th, 2020 at 12:45 am
One moment, please watch online adalat sony tv Kimberley Walsh likes to have some fun with her style, and usually opts for a statement piece with a quirky edge. We have recently seen her promoting her new book wearing whimsical pieces by the likes of Kandee, Kurt Geiger and Charlotte Olympia, but here, celebrating the birthday of bandmate Nicola in Amsterdam she is almost in danger of upstaging the birthday girl in this Henry Holland co-ord combo, which certainly makes a statement or two.
August 28th, 2020 at 12:46 am
Could I have , please? ketoforce uk Yesterday, Confidenti@l reported that Bieber was spotted at Chelsea hotspot 1Oak Tuesday, wearing bright blue capri sweatpants. Later that night, his security team lead two girls into the hotel, at 37th St. and Fifth Ave.
August 28th, 2020 at 12:46 am
How many are there in a book? prijs cialis Historian Anna Whitelock said: “William will only be the sort of second generation of royal fathers to actually be at the birth. Prince Charles was there at the birth of William and Harry, but before that the royal father would be elsewhere. Prince Phillip was playing squash when Prince Charles was born, so it wasn’t something that the fathers got involved with.”
August 28th, 2020 at 12:46 am
magic story very thanks where to buy periactin “These allegations are without merit and we stand by what we previously disclosed publicly in February 2011 - that BP natural gas traders did not engage in any market manipulation in late 2008,” BP spokesman Geoff Morrell said in a statement.
August 28th, 2020 at 12:47 am
International directory enquiries remboursement du viagra par la secu
“We had some good news out of China and Europe and theelections in Germany are favorable for the euro zone, but focusremains on the Fed,” said Peter Cardillo, chief market economistat Rockwell Global Capital in New York.
August 28th, 2020 at 12:47 am
Could I have an application form? what does wellbutrin cost without insurance Last year Apple also paid about $350 million for AuthenTec, a key player in fingerprint sensors and until its purchase a supplier to Samsung Electronics Co Ltd, Hewlett-Packard Co, Dell Inc, Lenovo Group Ltd and Fujitsu.
August 28th, 2020 at 12:47 am
The manager flagyl 500 mg once a day for 3 days However, because these children do exist, it should be as close to mandatory for all other children to be vaccinated - especially against measles
August 28th, 2020 at 12:48 am
Why did you come to ? proextender canada
Simon Maughan, head of sector strategy at OlivetreeFinancial Group, said the holding is part of Softbank which hasowned the stock since 2006, and is their entire holding, butanother part of Softbank owns a further 4.8 percent.
August 28th, 2020 at 12:50 am
Hello good day combivent online purchase Woodson also hinted that he doesnât expect to employ two point guards at the same time as he often did last season. Iman Shumpert, who took part in Mondayâs scrimmage after being limited a few days by a sore shoulder, figures to move from small forward and start alongside Felton in the backcourt to facilitate a switch to Carmelo Anthony, Tyson Chandler and newcomer Andrea Bargnani up front.
August 28th, 2020 at 12:51 am
I’m doing an internship where to get antabuse in south africa âItâs part of the game to lose guys, lose games,â running back Fred Jackson said. âYouâve got to come back and respond. Weâve got a good, extended period before our next game so hopefully we can get some guys back from injuries and do what weâve got to do to hit the ground running when we get to the next game.â
August 28th, 2020 at 12:52 am
We were at school together brittanellyn.com Prospects for that bill appear dim in the House, where Republicans remain opposed to the Senate’s plan, and where House Speaker John Boehner has declined to bring it to the floor for a vote. On Wednesday, House Republicans met to discuss immigration, and after their meeting GOP leaders voiced opposition to a comprehensive bill, preferring a “step-by-step” series of bills on border security and the immigration system.
August 28th, 2020 at 12:52 am
I’m in a band omeprazole cap 40mg High corn prices have made wheat a more viable alternative.POET Biorefining bought some wheat this year to grind intoethanol. Poultry and cattle producers this year are expected tofeed their animals record amounts of wheat, traditionally a cropreserved for human consumption.
August 28th, 2020 at 12:55 am
How much is a Second Class stamp? sveden viagra kaufen “The future would tell when the chairman (of the Federal Reserve) and his board deems that it’s appropriate, but for the moment, it’s clearly the approach that we’ve always recommended,” Lagarde said of the decision not to taper yet.
August 28th, 2020 at 12:55 am
I can’t stand football cialis best price online Emerging-market stocks rose to thehighest level in almost a month as Chinaâs economic growth metforecasts and the nation boosted foreign investor access to itsmarkets. Turkeyâs lira climbed as the central bank said itmay raise interest rates this month to bolster the currency.
August 28th, 2020 at 12:55 am
Have you got a telephone directory? purchase tricor online While Fisher has held reservations about the Fed’s bond-buying program, St. Louis Fed President James Bullard has saidhe is not prepared to start reducing the stimulus program,adding that there needs to be more economic data before movingto taper.
August 28th, 2020 at 12:55 am
Could you please repeat that? ec naprosyn generic The World Nuclear Association, an international organization that promotes nuclear power, endorses a limited discharge at Fukushima. “Tepco has been prevented from discharging any treated water due to political opposition,” the organization said in response to questions from Reuters. “Permitting sea release of treated water would alleviate the much larger problem of a demand for massive volumes of water storage.”
August 28th, 2020 at 12:56 am
I’ve lost my bank card how to get rid of side effects from cipro âIf they check that out, Madison Square Garden has had excellent relationships with all its unions. Weâve had no issues there at all. . . . Itâs more about politics and trying to gain an endorsement â to set the record straight,â Dolan said as Stern, seated to his right, grabbed the microphone.
August 28th, 2020 at 12:56 am
I’d like to order some foreign currency diflucan oral suspension dosage Rupert Murdoch has been recalled to face questioning by MPsafter a tape emerged on which he appeared to express regret overcooperation with police investigating his British newspapers anddescribe corrupt payments to public officials for information as”the culture of Fleet Street”.()
August 28th, 2020 at 12:57 am
I’m a partner in ketamine/baclofen/gabapentin/imipramine/nifedipine/tetracaine The Quaids were arrested over the weekend of Dec. 20, reported RadarOnline.com. There was a bench warrant out on the pair for failing to make a court appearance in connection with an unpaid hotel bill in Santa Barbara.
August 28th, 2020 at 12:57 am
I’m training to be an engineer valine at codon 600 Last month, a local Northern League councilor said Kyenge should be raped so she understands how victims of crimes committed by immigrants feel. The councilor has received a suspended jail sentence and a temporary ban from public office.
August 28th, 2020 at 12:58 am
I can’t hear you very well black russian terrier puppy imodium Levenson said he regrets the email sent to the team’s co-owners and general manager Danny Ferry two years ago as “inappropriate and offensive.” In a statement released by the team, Levenson said he sent the email due to his concerns about low attendance and a need to attract suburban whites.
August 28th, 2020 at 12:59 am
Would you like to leave a message? protonix or nexium Last year he raised his batting average from .242 in 2013 to .281, but because he walked only 20 times in 452 plate appearances, his .321 on-base percentage isn’t what teams want from the leadoff spot.
August 28th, 2020 at 12:59 am
We’d like to invite you for an interview side effects of trazodone in the elderly Regular gasoline averaged $3.66 a gallon on Long Island, New York, and $3.79 in Los Angeles.
August 28th, 2020 at 1:00 am
Go travelling can you buy propranolol online “These are laws that are causing human tragedies, and that’s what we are trying to show,” said Ladd Everitt, communications director for the Coalition to Stop Gun Violence. “This is something that not only affected the Martin and Zimmerman families but those who either saw or heard the events unfold.”
August 28th, 2020 at 1:00 am
Will I get paid for overtime? allopurinol 300 mg prices The political world also looks much more treacherous. Geopolitics has not yielded to the irresistible forward march of free market capitalism, and peace no longer looks like something to be taken for granted. The 9/11 attacks spawned wars in Afghanistan and Iraq â the kinds of conflicts that in 2000 were supposed to be a thing of the past.
August 28th, 2020 at 1:04 am
Could you transfer $1000 from my current account to my deposit account? buy singulair 10mg online Adrian Shandley, the head of Premier Wealth Management, said: “I do not see investing in Aim through Isas as something that you would do with your first, second or even third Isa unless you were a very informed investor. In order to reduce risk within Aim, you need to diversify and take professional advice.”
August 28th, 2020 at 1:04 am
Thanks for calling lisinopril for treatment of anxiety In this Aug. 27, 2013 photo, Madeleine and Jerry Bosco pose in their living room, with mostly inherited or thrift shop furnishings and a hardwood floor in need of refinishing or replacement, in the Tujunga area of Los Angeles. Now, five years after the recession, when Jerryâs pay was cut 15 percent and their home lost some of its value, theyâve had to cut back on necessities such as food, utilities, home repairs and new appliances, as well as extras such as weekend trips and dinners out. (AP Photo/Reed Saxon)
August 28th, 2020 at 1:04 am
How do you spell that? generic metformin cost John Coughlin, the 63-year-old brother of the Giants coach, died last week after falling while getting out of a cab after the Giantsâ loss at home to the Denver Broncos. His funeral will begin at 10 a.m. on Tuesday at St. Maryâs Church in Waterloo, about an hour west of Syracuse.
August 28th, 2020 at 1:04 am
A few months actos prices costco “Barring a major volcanic eruption, most 15-year global mean surface temperature trends in the near-term future will be larger than during 1998-2012,” according to the 127-page Technical Summary dated June 7 and obtained by Reuters.
August 28th, 2020 at 1:06 am
What sort of music do you like? buy enalapril 20 mg “We need to help our patients find social support throughout their illness,” he says. “If there isn’t a spouse to do that then we have to find other systems and networks to make that happen.”
August 28th, 2020 at 1:06 am
How do you do? buy neurontin 800mg no prescription There was much discussion about the dessert portion of the meal. When someone suggested he get a cookie, the president reminded the employees behind the counter that “I’m not on furlough” and was not eligible for their free cookie offer.
August 28th, 2020 at 1:07 am
Where are you calling from? accutane dosage 60 mg In New York, the Western-backed Syrian National Coalition told the U.N. Security Council it is ready to attend a peace conference if the Syrian government commits to having Assad hand over power to a transitional government.
August 28th, 2020 at 1:08 am
I don’t know what I want to do after university lovegra online bestellen I still think they have some hurdles to cross because I think they filed prematurely, said Ed McNeil, special assistant to the president of AFSCME Council 25. I dont think theyve proved insolvency. They have a list of people they cant pay, but theres an even bigger list of people they are still paying, and they have a bunch of friends and consultants getting paid. They havent been doing this process in good faith, and weve been saying that all along.
August 28th, 2020 at 1:09 am
Gloomy tales metoprolol withdrawl “Tears and defiance: Survivors return 70 years after liberation,” says the Guardian above its front page picture
August 28th, 2020 at 1:12 am
A First Class stamp zyban canada price But worsening violence has forced the community into a corner: Continuous clashes between the rebels and the regime in this isolated town of 2,000 people as well as other Christian towns over the past two weeks have many Christians worried that they will no longer be allowed to stay neutral.
August 28th, 2020 at 1:14 am
I love the theatre generic permethrin drugs “The outcome of this tribunal sends a strong and clear reminder to all accountants and accountancy firms that they have a responsibility to act in the public interest in the work they undertake,” said Paul George, executive director of conduct at the FRC.
August 28th, 2020 at 1:14 am
On another call cymbalta 60 mg cost The ability for the state to retain control with a minority equity ownership would have proved attractive for some of the state-owned enterprises. But for shareholders in Hong Kong and globally, it may be less so. The principle of treating all shareholders equally is what the Hong Kong regulator is protecting.
August 28th, 2020 at 1:14 am
We work together lisinopril tablet Wakil Ahmad Muttawakil, who served as foreign minister for the Taliban when the group ruled Afghanistan, also hailed Bardar’s release and cautioned Pakistan not to try to control his movements now that he is free.
August 28th, 2020 at 1:14 am
this post is fantastic escitalopram 10 mg overdose But several experts said the deal could ultimately go through with American and US Airways surrendering some overlapping routes at Reagan National Airport and elsewhere, and perhaps giving up a some planes or a hub.
August 28th, 2020 at 1:15 am
Is there ? cialis online canada paypal After hitting Manuel, Gipson pumped his fist and stared in the direction of the quarterback on the ground. Bills center Eric Wood called some Browns players âclasslessâ for the way they reacted to Manuelâs injury.
August 28th, 2020 at 1:15 am
Could I have a statement, please? beconase aquosum
Under SolarWorld’s debt restructuring deal, Qatar Solar willinvest 35 million euros in SolarWorld, becoming a 29-percentshareholder in the group, while existing shareholders will endup with 5 percent.
August 28th, 2020 at 1:17 am
I can’t get a signal trying to conceive while taking bactrim Now we don’t build things (an exaggeration, of course: the UK’s manufacturing base is nowhere near as deflated as anti-Thatcher comedians would have you believe) but we still make money by selling “services”, such as public text messaging on the web. It’s baffling to me how that works, though, ontologically, I have to accept that it does (the concept of a multibillion-pound Twitter makes a multibillion-pound Twitter a reality). It’s no less weird than a mania for tulips, is it?
August 28th, 2020 at 1:17 am
I’d like to transfer some money to this account protonix 80 mg bid
âWhen you take something like jalapeno lime salt and add it to a lotus root chip, it elevates it with more than a one-dimensional flavor,â says chef Carmine Di Giovanni of Greenwich Project in Greenwich Village. âIt also saves on ingredients â sliced tomatoes with flavored salt is unique and only two ingredients.â
August 28th, 2020 at 1:19 am
I can’t get a signal nizagara safe
The USGS elevation data was part of a series of about 400 updated maps released earlier in September by the agency, which is updating and refining all of Alaska’s topographic maps, some of which have been used for decades.
August 28th, 2020 at 1:20 am
I’d like to order some foreign currency how long does oral clindamycin take to work for acne
“It’s high time PC users in the UK started getting back the time they are losing to slow computers,” said Stefan Kratzer, senior product marketing manager at SanDisk USB & SSD.
August 28th, 2020 at 1:20 am
this is be cool buy etodolac no prescription Environmentalists have long pushed for banning plastic bags,which are cheaper for supermarkets to use than paper bags, butcreate mountains of trash
buy etodolac no prescription Environmentalists have long pushed for banning plastic bags,which are cheaper for supermarkets to use than paper bags, butcreate mountains of trash
August 28th, 2020 at 1:20 am
magic story very thanks premarin tablets cost
“You must remember, there were many people praying there - many, many people,” Dowling told CNA. “I was probably part of the answer to their prayers … (but) I did not say anything like the machinery would begin to work, or they would succeed in getting her out of the car.”
August 28th, 2020 at 1:23 am
I support Manchester United lamisil gel price George R.R. Martin, the author of the book series behind HBO’s ‘Game of Thrones’ is a big fan of ‘Breaking Bad.’ In fact, he says Walter White is a bigger monster than anyone in ‘Game of Thrones’ and claims that he wants to ‘do something about that.’ Gillian Pensavalle (@GillianWithaG) thinks there are plenty of monsters in ‘Game of Thrones.’
August 28th, 2020 at 1:23 am
Enter your PIN dapoxetine india brand “Well again, it’s been (an) even competition, we’ve been rotation days and things like that. Certainly he’s the incumbent,” said Ryan. “We’ll see how it goes from here. It seemed the natural thing to do.”
August 28th, 2020 at 1:23 am
Which team do you support? 25 mg seroquel as a sleep aid The IOC banned the country in December after refusing to recognize the results of Indian Olympic Association (IOA) elections due to government interference, which led to a tainted official being named its secretary general.
August 28th, 2020 at 1:24 am
The manager pharma-excipients.ch Power consumption in China, the world’s top energy user, isexpected to grow more than 9 percent this year, faster than the5.5-percent growth rate in 2012, the State ElectricityRegulatory Commission said in January.
August 28th, 2020 at 1:24 am
I don’t like pubs prevacid otc costco This leaves businesses with a single choice: More customer self-service â and fewer entry-level jobs for the people who need them. Thatâs why itâs tragic but not surprising to hear the story of a café owner in Brooklyn who warned last year that an increase in New Yorkâs minimum wage would leave her no option but to cut one-third of her staff.
August 28th, 2020 at 1:24 am
The National Gallery dapoxetine alternative While shutdown concerns have pressured equities over thepast two weeks, the S&P 500 index has frequently foundsupport at its 50-day moving average of 1,679.61, though itclosed slightly below that level on Thursday.
August 28th, 2020 at 1:25 am
Best Site Good Work clomid uk nhs The big three, already unhappy that Verizon may be set up aCanadian operation, say the auction rules would unfairly favorthe U.S. company. They have launched a high-profile publicrelations campaign to persuade Ottawa to change its mind.
August 28th, 2020 at 1:25 am
It’s serious cymbalta dose for pain management If William and Kate stick to tradition, it’s likely they’ll give their baby boy more than one name — William’s full name is William Arthur Phillip Louis, while his brother, Harry, is Henry Charles Albert David. Their father, the Prince of Wales, is Charles Phillip Arthur George, and Queen Elizabeth II was born Elizabeth Alexandra Mary.
August 28th, 2020 at 1:26 am
We work together xenical orlistat user reviews China is a critical region for Yum, accounting for more than 40 percent of the company’s operating profit. But sales at restaurants open at least began nose-diving after a TV report late last year said some of the company’s suppliers were giving chickens unapproved levels of antibiotics. A few months later, the chain’s recovery efforts were derailed by a bird flu scare.
August 28th, 2020 at 1:28 am
What qualifications have you got? how many milligrams of benadryl to get you high In July, Motorola forecast revenue to be flat to up 1percent this year. That was the second time it cut its forecast,both times blaming delayed purchases by its enterprise, ratherthan government, customers.
August 28th, 2020 at 1:29 am
Punk not dead abilify cheaper alternative The six million barrels are more than half Enbridge’s totalcapacity of around 11 million barrels at Hardisty, the tiny townin east-central Alberta that is Canada’s equivalent to Cushing,the main U.S. crude storage hub in Oklahoma.
August 28th, 2020 at 1:31 am
What do you like doing in your spare time? cnn singulair Judicial pensions also went up and back pay totaling about $250 million was provided to make up for the denied salary increases.
August 28th, 2020 at 1:32 am
I don’t know what I want to do after university salmeterol.cheapmeddrugs.org Whether the latest centre-right threats amount to more thanbluster is difficult to assess given a series of contradictorysignals from Berlusconi’s allies in parliament, who are dividedbetween a faction of hardliners and more conciliatory doves.
August 28th, 2020 at 1:33 am
Could you send me an application form? cheep levitra
‘Winter’s Bone’ isn’t really accurate - at least when it comes to showcasing Jennifer Lawrence’s natural beauty. But the film did lead to an Oscar nomination for the rising newcomer. Now the starlet’s stunning good looks are on full display in the May issue of GQ, where Lawrence stripped down to her skivvies.
August 28th, 2020 at 1:33 am
Just over two years can you get high on zyrtec Just as every family is different, each conversation takes its own course. But the group provides a starter kit to help people consider when and where to discuss the subject and key topics to cover. A scale of 1 to 5, for example, helps people identify the extent to which they want to be surrounded by loved ones at the time of death, whether quality of life supersedes quantity of years and whether they are more worried about getting insufficient or overly aggressive care. It also offers ice breakers with prompts like, “I need your help with something,” and supportive tips like, “You don’t have to steer the conversation; just let it happen.”
August 28th, 2020 at 1:36 am
I’m doing a phd in chemistry acticin dermal cream When questioned about his defense of Textor, Zimmerman admitted to sleeping on the job, said he suffered from sleep apnea, but still rated his performance in the case as an eight or nine out of 10. Assistant District Attorney Sammy McCrary showed sympathy with Textor, and reinstated his original plea offer, which Wigington readily accepted.
August 28th, 2020 at 1:37 am
I can’t get a dialling tone keflex 750 mg Many of those conservatives want a similar condition placedon raising the debt ceiling, but in his list of debt-ceilingdemands Sunday, Boehner did not mention the Affordable Care Act,commonly known as Obamacare.
August 28th, 2020 at 1:44 am
How would you like the money? doxycycline online canada Jonathan Lewis, an antitrust lawyer in Washington, calledthe Justice Department’s suit “very powerful” because it quotescompany documents and executives anticipating higher pricesthrough consolidation.
August 28th, 2020 at 1:45 am
Insufficient funds order pantoprazole Twitter now lets marketers pay to give their tweets prominent placement on timelines, where people get updates from the accounts they follow. The company also lets advertisers pay to be placed next to a list of popular topics on Twitter in different geographies.
August 28th, 2020 at 1:51 am
Could you tell me my balance, please? what is the cost of iv tylenol Global funds may not just stop pouring in - since February,investors have been pulling money out of Asia-dedicated funds.While foreign investors are still buying stocks in Japan, theyhave sold at least $10 billion worth of stocks in the rest ofAsia in the past 13 weeks, according to Nomura.
August 28th, 2020 at 1:59 am
I’d like to change some money atorvastatin calcium 20mg tablet Fred’s Inc, a small discount chain, said promotionswere what lifted same-store above expectations sales last month.Cato Corp, which sells clothing, reported a 5 percentdecline that Chief Executive Officer John Cato blamed on”continuing economic uncertainty.”
August 28th, 2020 at 2:02 am
Canada>Canada how to stop taking cymbalta 30 mg Plaque psoriasis is thought to be caused by an inflammatory response initiated by the body’s immune system and affects about 125 million people. Those suffering from the disease are also at a greater risk of developing diabetes and heart disease.
August 28th, 2020 at 2:07 am
A company car order carvedilol WASHINGTONâSamantha Power, the genocide crusader nominated to serve as the U.S. representative to the United Nations, vowed to be a “blunt, outspoken champion of American values” if confirmed for a job that will test U.S. relationships with countries that have competing international interests.
August 28th, 2020 at 2:07 am
Sorry, I’m busy at the moment reglan for increasing breast milk supply “I think that the president believes that Republican leaders in general and Republicans in general do not want to see the nation go down that path again,” White House spokesman Jay Carney told reporters. “But it requires leadership to ensure that minorities of minorities or — minorities of majorities — don’t bring about an unforeseen result. But this is up to Congress to resolve. Again, it is not something that should be negotiated. That is the responsibility of Congress to pay the bills that it’s already racked up.”
August 28th, 2020 at 2:15 am
This site is crazy keflex order online Although the complaints in New York state court gave Rodriguez some temporary control of the narrative for the first time in months, those appearances can be deceiving. With his lawsuit against MLB in particular, Alex Rodriguez is following Armstrong down the disastrous road the fallen cyclist took last year in his own bid to escape a doping ban. The Rodriguez complaint even borrows the term âwitch huntâ that was such a standby for Armstrong before he surrendered his fight with the U.S. Anti-Doping Agency.
keflex order online Although the complaints in New York state court gave Rodriguez some temporary control of the narrative for the first time in months, those appearances can be deceiving. With his lawsuit against MLB in particular, Alex Rodriguez is following Armstrong down the disastrous road the fallen cyclist took last year in his own bid to escape a doping ban. The Rodriguez complaint even borrows the term âwitch huntâ that was such a standby for Armstrong before he surrendered his fight with the U.S. Anti-Doping Agency.
August 28th, 2020 at 2:16 am
Special Delivery can you buy clomid on the internet U.S. Secretary of State John Kerry said he looked forward toa “good meeting” with Iran and major powers on Thursday, and aU.S. official said China agreed that Iran should respondpositively to existing proposals on Iran’s nuclear program.
August 28th, 2020 at 2:19 am
I’m doing a masters in law motility boost uk The organisation and other animal welfare groups say conditions on such “farms”, where puppies are bred in large numbers for profit, are often very poor, with animals subjected to overcrowding and a poor diet, meaning diseases are rife.
August 28th, 2020 at 3:34 am
Where do you come from? how to buy celebrex online The same submarine was hit by an explosion in 2010 that killed one sailor and injured two others. The navy said that accident was caused by a faulty battery valve that leaked hydrogen, causing an explosion in the vessel’s battery compartment. There have been no details on what caused this week’s blasts.
August 28th, 2020 at 3:59 am
I’m at Liverpool University glucophage 1000 mg xr Should the Fed continue to purchase mortgage-backed securities at current rates, there is a chance mortgage rates could actually head lower, said Keith Gumbinger of HSH.com, a mortgage information provider.
August 28th, 2020 at 4:17 am
good material thanks levofloxacin 500 mg tab
Serco Inc, U.S. subsidiary of Serco Group Plc, willhelp review and process paper applications from consumers whoapply for subsidized insurance coverage through federallyoperated exchanges in 34 states, according to the 12-yearcontract awarded by the Department of Health and Human Services.
August 28th, 2020 at 4:24 am
order cleocin
August 28th, 2020 at 4:54 am
dipyridamole buy online
August 28th, 2020 at 5:05 am
I’ll call back later orlistat diet pills uk But there are almost certainly other factors in play. As with surviving the Titanic disaster, good luck may play a role. Some people may simply wind up in circumstances that defend them against obesity. In some cases, it is personal commitment and resolve â and hard work. In some, there is defense at the level of genes. We are learning more and more about genetic variation â both our own and that of our resident microbes â with implications for energy balance and weight regulation. Some of us are genetically more disposed to gain weight, others less. Those at the extreme of the bell curve may find weight gain nearly impossible; most of us know a person or two like that, although they are very much in the minority.
August 28th, 2020 at 5:15 am
lopressor 6.25
August 28th, 2020 at 5:57 am
No, I’m not particularly sporty buspar reviews 2013 He said that eventual improvements to the environment and economic benefits of the quarry extension “would clearly outweigh the loss of the ancient woodland and the other adverse effects of the development in this case”.
August 28th, 2020 at 6:04 am
I’ve just started at symptoms of getting off zyprexa In a packed courtroom, supporters of the defendants noisily voiced their anger at the upheld convictions as the chief judge spoke, chanting the secularist slogan “we are Mustafa Kemal’s soldiers” and “Tayyip will answer to the people”.
August 28th, 2020 at 6:12 am
We’ll need to take up references how to get pregnant on clomid and metformin
Equity markets have been closely tied to central bankpolicy, with many investors concerned that economic growth isn’trobust enough to boost stocks without the Fed’s help. Last week,the July payroll report was much weaker than expected.
August 28th, 2020 at 6:55 am
What line of work are you in? olanzapine ocd “In 2000, I wanted a piece of Vijay Singh and I was able to get that,” Woods said. “You can do things of that nature. You can get guys who have been battling for a number of years, who have rivalries, you can put them out there.”
August 28th, 2020 at 7:04 am
What are the hours of work? propecia 1mg tablets price in india
LONDON (Alliance News) - Betting company William Hill PLC Thursday warned that operating profit was GBP20 million below its expectations in its third quarter and it may not make up the shortfall before the end of the year, after results, particularly football scores, went against it.
August 28th, 2020 at 8:05 am
It’s a bad line terbinafine tablets price uk Grouped into three, separate sultanates, the Muslims in southern Philippines fought Spanish colonization for centuries. It was not until right before the advent of American annexation, in 1898, that Spain managed to conquer all of the large island of Mindanao and defeat the last sultan of Sulu.
August 28th, 2020 at 8:22 am
Could I take your name and number, please? getting off effexor naturally Tushar Morzaria, a Ugandan who came with his family to the UK in 1971 when he was a boy, will replace Chris Lucas as finance director in a move that sees the last of the Barclays old guard replaced in the boardroom.
August 28th, 2020 at 8:26 am
I’d like to send this to safe reliable cialis website Dames said he had been inspired by his previous work with schools and thinking about what he wanted to teach his daughter upon becoming a father 18 months ago. “If they [children] understand nature, they will value it and will take more care of it when they get older. If you’re not engaged with it, you’re not going to feel any need to safeguard it. I think outdoor learning is the only way to do that,” he said.
August 28th, 2020 at 8:36 am
What do you want to do when you’ve finished? can a child take claritin and ibuprofen together “Weâre anticipating opening another tiki-themed bar, not necessarily a PKny 2.0 version, but more of a mid-20th century classic tiki bar,” former PKny bar manager Nathan Holland told the Daily News.
August 28th, 2020 at 9:01 am
augmentin tablets 375mg
August 28th, 2020 at 9:14 am
buy baclofen online usa
August 28th, 2020 at 9:22 am
How many would you like? methylprednisolone 80 mg ndc number LOL If itâs coming this Fall it would have been announced long ago. Iâve seen too many websites with false information. Iâve heard people say even retailers ask you if you wanna pre-order the PC version, theyâre misinformed and donât know more than us.
August 28th, 2020 at 9:35 am
I’m doing a masters in law autre utilisation du viagra Financial incentives to put people on the regime will also be scrapped. Dr Kiely has previously stressed that there were no financial targets for Calderdale and Huddersfield.
August 28th, 2020 at 10:30 am
A few months dapsone gel dermatitis herpetiformis “If the liquid comes into contact with the eyes it can cause conjunctivitis, eye pain and damage to the cornea potentially resulting in temporary blindness
August 28th, 2020 at 10:50 am
Enter your PIN buy cialis online from canada Sri Lanka suspended milk powder imports from New Zealand, while Brunei media cited its government as ordering a recall and the ban on the import, distribution and sale of Fonterra food products. Fonterra has not identified either of those countries as having been affected by the safety issue, though it has said products containing the contaminated whey protein had been sold on to Malaysia, Saudi Arabia and Thailand.
August 28th, 2020 at 10:52 am
I’ll text you later lopressor 12.5 mg Western powers on the Security Council backed away from many of their initial demands, diplomats say, in order to secure Russia’s approval. Russian Foreign Minister Sergei Lavrov said an “understanding” had been hammered out, but gave no details.
August 28th, 2020 at 11:17 am
strattera india
August 28th, 2020 at 11:29 am
Where did you go to university? renova costruzioni With Clowe, the Devils are taking a huge risk signing him to such a long-term deal after a mostly disappointing season with two suspected concussions sustained this year with Rangers (one late regular season in Carolina, another in playoffs against Capitals). Clowe, 30, just had three goals in 12 regular-season games.
August 28th, 2020 at 11:47 am
just like to say cheers for a remarkable post and a all round interesting blog (I also love the theme/design), I don at have time to look over it all at the
August 28th, 2020 at 12:50 pm
order cialis 10mg
August 28th, 2020 at 2:10 pm
Not available at the moment risperidone 1 mg tab zyd NASA scientists have been studying the melting rates of Arctic ice since decades. Studying the updates of Arctic ice and its melting pattern, Arctic loses 30,000 square miles of sea ice each year. Last year’s melting rate was very high and the NASA scientists had reported a record low in the amount of ice available. It was noticed in 2012 that the ice cap of the Arctic Ocean reduced to its lowest extent ever recorded.
August 28th, 2020 at 2:39 pm
There is certainly a lot to find out about this topic. I like all the points you made.
August 28th, 2020 at 2:50 pm
Which year are you in? how do you wean off dilantin Members of the House Committee on Energy and Commerce wroteto Smithfield on July 24 asking the company to turn overinformation on its production of crude heparin, the rawingredient used to make the drug.
August 28th, 2020 at 4:30 pm
I’m a trainee triverex canada
Attorneys and the judge were concerned that the Florida case, which ended Saturday with Zimmerman’s acquittal in the death of Trayvon Martin, would unduly influence the jury, which was selected on Monday.
August 28th, 2020 at 5:05 pm
lisinopril 1 mg
August 28th, 2020 at 5:48 pm
disulfiram uk
August 28th, 2020 at 6:19 pm
pretty helpful material, overall I believe this is well worth a bookmark, thanks
August 28th, 2020 at 6:37 pm
propecia brand
August 28th, 2020 at 7:36 pm
Will I be paid weekly or monthly? le viagra dure combien de temp
But the government says the pilot scheme specifically targets illegal immigrants and highlights the advantages for them of returning to their home country voluntarily. It also says it is much cheaper to get people to return home of their own accord rather than fight deportation through the courts.
August 28th, 2020 at 8:03 pm
Jordan 4 Retro…
http://www.jerseysbasketball.us/ Basketball Jerseys…
August 28th, 2020 at 8:52 pm
I’d like to cancel a cheque buy female viagra in uk
Under current LME rules, warehouse companies with more than900,000 tonnes in one location are required to load out metal ata minimum rate of just 3,000 tonnes per day, regardless of howmuch is delivered into the facility.